5. Стержень, балка, вал, брус, пластина, плита, оболочка.

Брусом называется геометрический объект, одно из измерений которого (длина) много больше двух других. Геометрически брус может быть образован путем перемеще­ния плоской фигуры вдоль некоторой кривой, как это показано на рис. 1.1.

Эта кривая называется осью бруса, а плоская замкнутая фигура, распола­гающая свой центр тяжести на оси бруса и нормальная к ней, называется его поперечным сечением. Брус может иметь как постоянное, так и переменное поперечное сечение. Многие сложные конструкции на практике рассматриваются как комбинации элементов, имеющих форму бру­са, поэтому в настоящей книге преимущественно рассматриваются методы расчета бруса как основного геометрического объекта изучения науки со­противления материалов. Брус, работающий при растяжении, называется стержнем, при изгибе – балкой, при кручении – валом. Стержневые элементы, воспринимающие вертикальные сжимающие силы, называют стойками, а наклонные элементы - раскосами. Конструкцию, состоящую из соединенных изгибаемых стержней, называют рамой. Если же благодаря шарнирному соединению стержней все они работают только на растяжение или сжатие (от нагрузки, приложенной в узлах), то конструкцию называют фермой.

Второй основной геометрической фор­мой, рассматриваемой в сопротивлении материалов, является обо­лочка, под которой подразумевается тело, у которого одно из измерений (толщина) намного меньше, чем два других. К оболочкам относятся различного рода резервуары, котлы, купола зданий, корпуса подводных лодок, обшивка фюзеляжа самолета и т.п.

Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной. Примером могут служить крыши и днища резервуаров, перекрытия зданий, различные диски и т.п.

Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга, называется массивом. К ним относятся фундаменты сооружений, подпорные стенки и т.п.

6. Растяжение и сжатие стержней, принцип Сен-Венана, гипотеза плоских сечений.

Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

Принцип Сен-Венана: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.

В сопротивлении материалов этот принцип формулируется так: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагрузки и определяется лишь статическим эквивалентом нагрузки. Таким образом, этот принцип позволяет одни граничные условия (действующие силы) заменять другими (удобными для статичного расчёта) при условии, что равнодействующая и главный момент новой заданной системы сил не изменяется. Принцип используется также и при упругопластической деформации.

И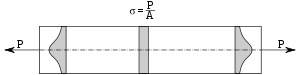 ллюстрацией принципа Сен-Венана является приведённый рисунок.

На примере стержня, растягиваемого точечно приложенными на обоих концах усилиями, видно, что в непосредственной близости от точек приложения распределение напряжений близко к рассмотренному характеру нагрузки. На достаточном расстоянии от концов распределение напряжений по сечению приближается к равномерному.

Принцип Сен-Венана освобождает от необходимости рассмотрения большого количества возможных вариантов статически эквивалентных нагрузок. В то же время вопрос о напряжениях и деформации поблизости точек приложения нагрузок остаётся открытым. Задачи подобного вида рассматриваются в специальных дисциплинах.

Растяжение и сжатие стержней. Растяжение-сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс).

Называется также одноосным или линейным напряжённым состоянием. Является одним из основных видов напряжённого состояния параллелепипеда. Может быть также двух- и трёх-осным^[1]. Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).

Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).

В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает т. н. внецентренное растяжение (сжатие). В этом случае за счёт эксцентриситета приложения нагрузки в стержне кроме растягивающих (сжимающих) напряжений возникают ещё и изгибные напряжения.

Н апряжение вдоль оси прямо пропорционально растягивающей или сжимающей силе и обратно пропорционально площади поперечного сечения. При упругой деформации между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их накоэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами.

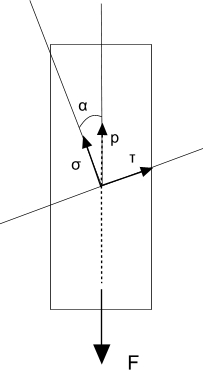
Напряжения в растянутом или сжатом стержне.

Рис.1

Рассмотрим прямолинейный стержень постоянного сечения, растягиваемый (сжимаемый) двумя противоположно направленными силами. Используя гипотезу о равномерности распределения напряжений, рассмотрим равновесие некоторой части стержня, отсеченной плоскостью a-a, нормаль которой наклонена к оси стержня под углом α. Внешняя сила F уравновешивается напряжениями, равномерно распределенными по площади наклонного сечения A_α. Обозначив площадь поперечного сечения, перпендикулярную к оси стержня, за A₀, для  . Составив условие равновесия отсеченно части стержня, получим: pA_α−F=0, откуда следует выражение

Разложим напряжения p на нормальную σ_α и касательную составляющие.