26. Гипотеза де- Бройля. Волновая функция. Уравнение Шредингера

Французский физик Луи де Бройль высказал гипотезу о том, что установленный ранее для фотонов корпускулярно-волновой дуализм присущ всем частицам — электронам, протонам, атомам и так далее. Таким образом, если частица имеет энергию Е и импульс, абсолютное значение которого равно р, то с ней связана волна, частота которой и длина волны , где h— постоянная Планка. Эти волны и получили название волн де Бройля.

Для частиц не очень высокой энергии, движущихся со скоростью (скорости света), импульс равен (где m — масса частицы), и . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10−2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться.

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы. Для свободной частицы с точно заданным импульсом p(и энергией E), движущейся вдоль оси x, волновая функция имеет вид: где t — время, .В этом случае , то есть вероятность обнаружить частицу в любой точке одинакова.

В координатном представлении волновая функция зависит от координат системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности обнаружить систему в положении, описываемом координатами в момент времени : .Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области конфигурационного пространства конечного объема :

Зависящее от времени уравнение Шрёдингера где ,  — постоянная Планка;  — масса частицы,  — внешняя по отношению к частице потенциальная энергия в точке в момент времени

27. Квантование энергии на примере частицы в бесконечно глубокой потенциальной яме

Проведем анализ решений уравнения Шредингера применительно к частице в одномерной пря­моугольной «потенциальной яме» с бесконечно высокими «стенками». 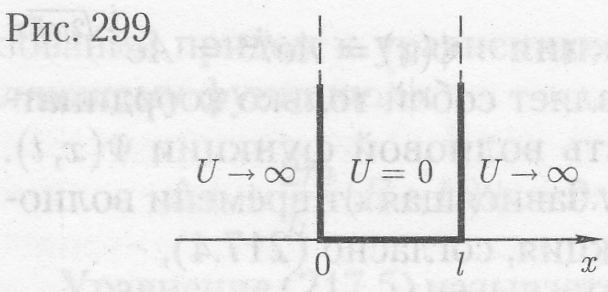Та­кая «яма» описывается потенциальной энергией вида (для простоты принима­ем, что частица движется вдоль оси х) 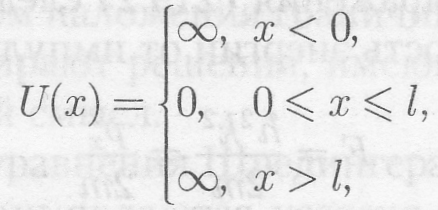где L — ширина «ямы», а энергия отсчи­тывается от ее дна (рис. 299).

Уравнение Шредингера (217.5) для стационарных состояний в случае одно­мерной задачи запишется в виде

По условию задачи (бесконечно вы­сокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и вол­новая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=L) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло­вия в данном случае имеют вид

В пределах «ямы» урав­нение Шредингера (220.1) сведется к уравнению

или

где

Общее решение дифференциально­го уравнения (220.3):

Так как по (220.2)

Тогда

Условие (220.2) выполняется только при kl=nπ, где п — целые числа, т. е. необходимо, чтобы

Из выражений (220.4) и (220.6) сле­дует, что

т.е. стационарное уравнение Шредин­гера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяет­ся только при собственных значени­ях Е_п, зависящих от целого числа п. Следовательно, энергия Е_п частицы в «потенциальной яме» с бесконечно вы­сокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется.