Тема 1.З. Агрегатные состояния вещества и фазовые переходы

Задача 13. Температура воздуха 20°С, а температура точки росы 8°С. Найти абсолютную и относительную влажности воздуха.

Дано: t=20°С — температура воздуха; t_р=8°С — температура точки росы.

Найти: р — абсолютную влажность; В — относительную влажность воздуха.

Решение. Для решения задач на определение влажности воздуха необходимо воспользоваться таблицей "Давление насыщающих водяных паров и их плотность при различных температурах". Температуре точки росы 8°С соответствует по таблице плотность 8,3·10^-3 кг/м³ .Это и будет абсолютная влажность р. Относительную влажность определим по формуле

В=(ρ/ρ_н)100 %,

ρ_н — насыщающих паров при температуре 20°С равна 17,3·10 кг/м³ по таблице, следовательно,

Ответ. Абсолютная влажность воздуха 8,3 • 10 ³ кг/м³, относительная влажность приблизительно 48 %.

Задача 14. Днем при температуре 20°С относительная влажность воздуха была 60%. Какое количество воды в виде росы выделится из 1 м³ воздуха, если ночью температура понизится до 8°С.

Дано: В=60% — относительная влажность воздуха; t₁=20°С и t₂=8°С — температура воздуха соответственно днем и ночью.

Найти: m — массу воды, выделившейся из 1 м³ воздуха.

Решение. Определим абсолютную влажность :

В=(ρ/ρ_н)100 %, =В _н/100%

где ρ_н=17,3·10^-3 кг/м³ (взято из таблицы). Тогда

По той же таблице находим, что при 8°С в 1 м³ может содержаться не более 8,3·10^-3 кг влаги, следовательно, излишек выпадет в виде росы:

Δт=(10,4-8,3)·10^-3 кг/м³·1 м³=2,1·10^-3 кг=2,1 г.

Примечание. Зная объем помещения, можно определить массу сконденсированных водяных паров из всего объема помещения.

Ответ. Вследствие понижения температуры из 1 м³ воздуха выделится 2,1 г воды.

Задача 15. Относительная влажность воздуха 74 %, а его температура 20°С. Что показывает влажный термометр психрометра? Какова абсолютная влажность воздуха?

Дано: B=74%=0,74 — относительная влажность воздуха; t = 20°С — температура воздуха.

Найти: t_вл — показание влажного термометра; — абсолютную влажность воздуха.

Решение. Для решения задачи необходимо воспользоваться психрометрической таблицей. Найдем в первой графе показание сухого термометра 20°С — это температура воздуха. В этой же строке найдем относительную влажность 74%. Она находится в графе с разностью температур сухого и влажного термометров, равной 3°С. Отсюда t- t_вл=3°С, следовательно,

t_вл=t -3°С, t_вл=20°С-3°С=17°С.

Для нахождения абсолютной влажности обратимся к таблице "Давление насыщающих водяных паров и их плотность при различных температурах". Из таблицы находим ρ_н — плотность насыщающих водяных паров при 20°С: _н=17,3·10^-3 кг/м³.

Используя формулу относительной влажности В=ρ/ρ_н, найдем

ρ=В_нρ_н, ρ=0,74·17,3·10^-3 кг/м³=12,8·10^-3 кг/м³.

Ответ. Показание влажного термометра 17°С; абсолютная влажность воздуха 12,8·10^-3 кг/м³.

Задача 16. Определить, сколько воды при температуре 12°С можно обратить в пар при 100°С за счет теплоты, полученной при сжигании 1 кг нефти. КПД кипятильника 80 %.

Дано: t₁=12°С — начальная температура воды; t₂=100°С — температура пара; т_н=1 кг — масса нефти; η=80 %=0,8 — КПД кипятильника; с_в=4187 4190 Дж/(кг·К) — удельная теплоемкость воды; r=2,26·10⁶ Дж/кг — удельная теплота парообразования воды; q=4,6·10⁷ Дж/ кг — удельная теплота сгорания топлива.

Найти: т_в — массу воды, обращенной в пар.

Решение. Запишем формулу КПД: η=Q_п/Q_з На нагревание воды до 100°С и ее обращение в пар расходуется теплота: Q_n=c_Bm_B(t₂—i₁)+rт_в. Затраченная теплота Q₃=qm_H, следовательно,

Q_n=ηQ_з, т.е. m_в[с_в(t₂ –t₁)+r]=ηqт_н, отсюда

Ответ. В кипятильнике можно нагреть до 100°С и обратить в пар 14 кг воды.

Задачи для самостоятельного решения: № 5.33-5.40, 5.43, 5.44, 5.48, 5.15-5.19, 5.23, 5.28-5.30.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Дайте определение процессам испарения и конденсации. Какой из них происходит с поглощением энергии? 2. Назовите свойства насыщающих паров. Применимы ли к ним законы для идеальных газов? 3. Какой процесс называется кипением? Запишите уравнение теплового баланса для процесса парообразования. 4. Дайте определение абсолютной и относительной влажности. 5. Что такое точка росы? 6. Какие приборы для определения влажности воздуха Вы знаете? 7. Какое состояние вещества называется критическим? 8. В чем состоит отличие жидкостей от газов? 9. Как объяснить возникновение сил поверхностного натяжения? 10. Дайте определение поверхностному натяжению. 11. Как ведут себя смачивающие и несмачивающие жидкости в капиллярах? Приведите примеры из жизни. 12. Что Вам известно об аморфных телах?

Задача 17. К свободному концу вертикально закрепленной проволоки подвесили груз массой 2,26 кг, после чего ее длина увеличилась на 0,6 мм. Первоначальная длина проволоки 3 м; ее диаметр 0,8 мм. Определить механическое напряжение, относительное удлинение провода и модуль упругости (модуль Юнга) материала.

Дано: m= 2,26 кг — масса груза; l=0,6 мм=6·10^-4 м — удлинение проволоки; l=3 м — первоначальная длина проволоки; d=0,8 мм=8·10^-4 м — диаметр проволоки.

Найти: σ — механическое напряжение проволоки; ε — относительное удлинение; Е — модуль упругости (модуль Юнга) материала проволоки.

Решение. Механическое напряжение σ равно отношению силы упругости F= mg к площади поперечного сечения S= d²/4.

Относительное удлинение определим из соотношения

Для определения модуля упругости используем закон Гука ε=σ/E:

Е=44·10⁶ Па/2·10^-4=22·10¹⁰ Па=220 ГПа.

Ответ. Напряжение равно 44 МПа; относительное удлинение 2·10^-4; модуль Юнга 220 ГПа.

Задача 18. Мостовая железная ферма при 0°С имеет длину 100 м. На сколько изменится длина фермы при понижении температуры до -30°С?

Дано: t₀=0°С — начальная температура фермы; l₀=100 м — первоначальная длина; t=-30°С — конечная температура фермы; α=1,2·10^-5 К^-1 — температурный коэффициент линейного расширения материала фермы.

Найти: Δl — изменение длины.

Решение. Из формулы для температурного коэффициента линейного расширения имеем: Δl =αl₀ t, где t=t- t₀, t=-30 К;

Δl=1,2·10^-5 К^-1·100 м·(-30 К)=-3,6·10^-2 м.

Знак минус указывает на то, что произошло уменьшение длины.

Ответ. Длина фермы уменьшилась на 3,6 см.

Задача 19. Вычислить плотность ртути при 50°С.

Дано: t=50°С — температура ртути; β=1,8·10^-4 К^-1 — температурный коэффициент объемного расширения ртути.

Найти: ρ — плотность ртути при заданной температуре.

Решение. Для решения задачи воспользуемся формулой зависимости плотности вещества от температуры ρ=ρ₀/(1+ t) (здесь ρ₀=1,36·10⁴ кг/м³ — табличное значение плотности, взятое при 0°С, a Δt — разность температур, которым соответствуют плотности ρ₀ и : Δt=50°С=50 К);

Ответ. Плотность ртути при 50°С приблизительно 1,35·10⁴ кг/м³.

Задачи для самостоятельного решения: № 7.12-7.20, 8.11-8.19, 7.69, 7.76, 7.83, 7.86, 8.9, 8.12, 8.15, 8.25, 8.29, 8.42,8.46.

Задача 20. Лед массой 1 кг при температуре 263 К необходимо обратить в воду при 373 К. Сколько потребуется израсходовать теплоты, если предположить, что процесс протекает без потерь энергии?

Дано: m=1кг — масса льда; T₁=263 К — начальная температура льда; с_л=2,1·10³ Дж/(кг·К) — удельная теплоемкость льда; Т₀=273 К — температура плавления льда; =3,35·10⁵ Дж/кг — удельная теплота плавления льда; Т₂=373 К — конечная температура воды; с_в=4,2·10³ Дж/(кг·К) — удельная теплоемкость воды.

Найти: Q — количество необходимой энергии.

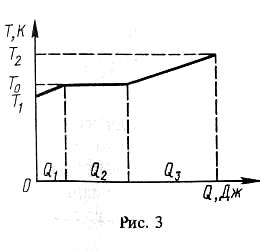
Решение. На рисунке представлен график процессов, соответствующих условию задачи. Общее количество теплоты равно сумме количеств теплоты, необходимой для повышения температуры льда до температуры плавления, для плавления и для нагревания полученной воды до температуры кипения. Обозначим эти количества теплоты соответственно через Q₁, Q₂ и Q₃. Тогда Q=Q₁+Q₂+Q₃. Так как Q₁=с_лт(Т₀-Т₁); Q₂= m; Q₃=с_вm(Т₂-T₀),то

Q=m[c_л(Т₀-Т₁)+ +с_в(Т₂-Т₀)],

Q=1 кг·[2,1·10³ Дж/(кг·К)·10 К+3,35·10⁵ Дж/кг+4,2·10³ Дж/(кг·К)·100 К] 7,8·10⁵ Дж 780 кДж.

Ответ. Необходимо израсходовать приблизительно 780 кДж.

Задача 21. Какое количество стали, взятой при 300 К, можно расплавить в печи с КПД 50 %, сжигая 2 т каменного угля марки А-1?

Дано: η=50 %=0,5 — КПД печи; Т₁=300 К — начальная температура стали; Т₀=1673 К — температура плавления стали; с=4,6·10² Дж/(кг·К) — удельная теплоемкость стали;λ=2,1·10⁵ Дж/кг — удельная теплота плавления стали; т_у=2 т =2000 кг — масса каменного угля; q=2,05·10⁷ Дж/кг — удельная теплота сгорания каменного угля.

Найти: т — массу стали.

Решение. Количество теплоты, необходимое для данного процесса, Q_n=rQ₃, где Q_n и Q_з — полезная и затраченная теплота;

Q_n=cm(Т₀ –T₁) + λm; Q₃=qm.

Составляя уравнение теплового баланса, определим т:

Ответ. Можно расплавить 24 т стали.

Задачи для самостоятельного решения: № 7.24—7.26, 7.34—7.36.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. В чем отличие твердых тел от жидкостей? Что необходимо для того, чтобы твердое кристаллическое тело начало плавиться? 2. Что называется удельной теплотой плавления? В каких единицах она выражается?

3. Как зависят температура и теплота плавления от внешнего давления?

4. Какая точка на диаграмме состояния вещества называется тройной?

5. Какова для воды температура тройной точки?