Глава 3.Тенденции и закономерности формирования себестоимости молока в регионе.
Раздел 3.1. Методика проверки информации на соответствие требований закона нормального распределения.
Для того чтобы провести корреляционный анализ необходимо строить корреляционные модели (КМ).
Корреляционная модель - математическое выражение, типов уравнений, показывающее количественную взаимосвязь между результативным показателем и формирующими его факторами.
В данной работе будет рассмотрено построение линейной многофакторной модели по группе хозяйств Могилевской области за отчетный 2010 годовой период для исследования формирования себестоимости молока (наш результативный показатель).
Выбрали следующие факторные показатели:
– среднегодовое поголовье, гол;
– оплата 1 чел/ч, тыс.руб.;
– удельный вес затрат на корма, %;
– удельный вес затрат на ОПФ, %;
– удельный вес затрат на энергоресурсы, %;
– затраты труда на 1 ц, чел/час.;
– получено приплода на 1 гол, гол;
– продуктивность, ц;
– удельный вес концентратов, %;
– удельный вес покупных кормов, %;
– расход ц.к.ед. на 1 ц, ц.к.ед.;
– стоимость кормов на 1 ц, тыс.руб.;
Общим требованием
к исходной информации для многофакторной
модели является выдержка соотношения
между числом опытов (n)
и числом факторов (k).
Число опытов (хозяйств) должно быть в
2,5 раз больше числа факторов, включая
результативный:
В нашем случае
n=153,
k=12
153>30, следовательно, исходная информация
удовлетворяет необходимому требованию
репрезентативности.
Требование однородности означает, что анализируемая информация должна быть взята из однотипных хозяйств. Иначе, в одну совокупность могут быть включены объекты, характер и цель деятельности которых резко отличаются. Использование разнородных объектов будет искажать характер связи между отдельными признаками. [4, с.274]. В исходную информацию должны быть включены данные хозяйств, имеющих примерно одну систему собственности, одно направление в специализации и т.д.
Информация по хозяйствам чаще всего является недостоверной, этому способствуют человеческие факторы, такие как невнимательность, безответственность и другие; также информация может содержать ошибки вследствие неточности при вычислениях, округлениях.
Информация является достоверной и репрезентативной в том случае, когда она отвечает закону нормального распределения.
Сущность закона в том, что по мере приближения варианта к среднему значению, вероятность его наступления возрастает.
Математически закон выглядит следующим образом:
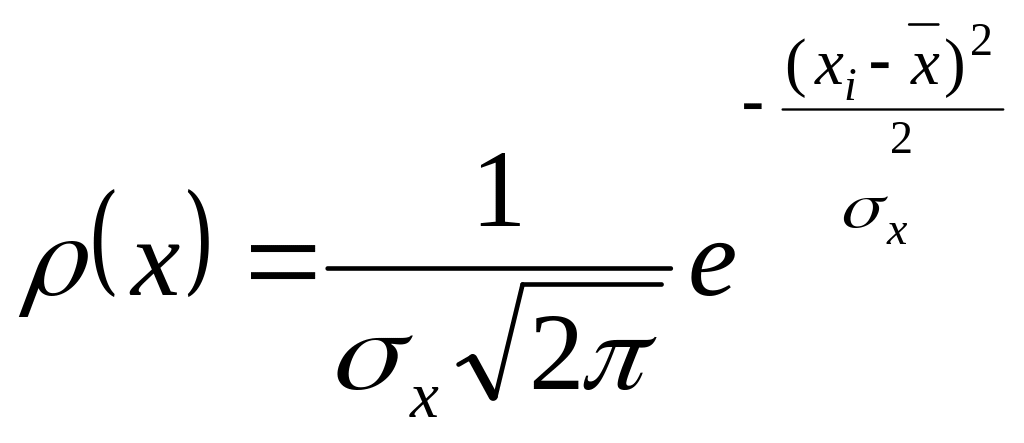
- среднеквадратическое
отклонение;
-
значение варианта фактора i;
-
среднее значение;
p(x) - вероятность появления варианты х.
Для того, чтобы проверить информацию на достоверность воспользуемся простейшими характеристиками ассиметрии (А) и эксцесса (Э), которые вычисляются по следующим формулам:
;
.
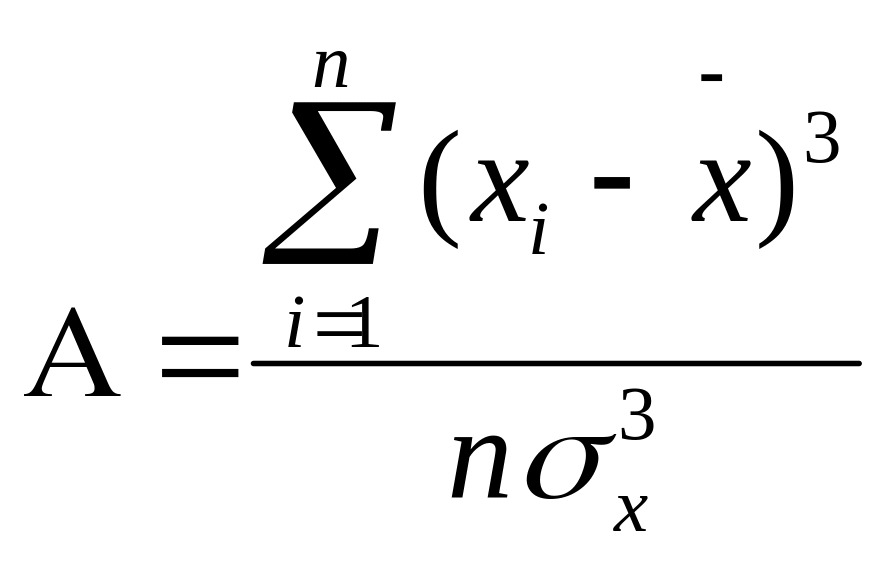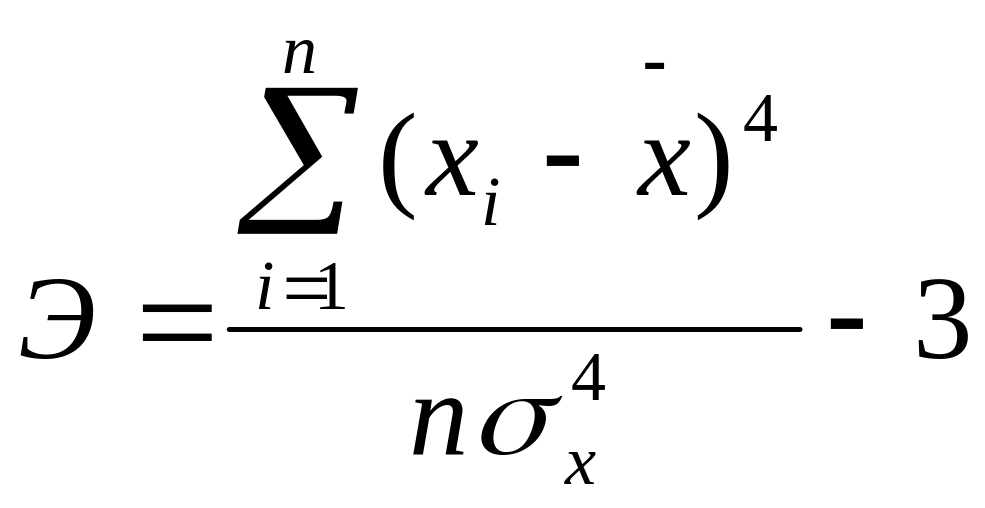На соответствие требованиям закона нормального распределения проверяется каждый из столбцов КМ, включая результативный. Если информация столбца отвечает требованиям закона нормального распределения, то его А и Э = 0.
В данной работе А и Э по каждому столбцу больше нуля, из чего следует, что экономическая информация содержит ошибки.
Следует считать, что информация не противоречит требованиям закона нормального распределения, если А и Э не выходят за допускаемые пределы:
|A|≤3σА,
где
,
где n – количество наблюдений;
– среднее
квадратическое отклонение по асимметрии;
|Э|≤5
где
,
где n – количество наблюдений;
– среднее квадратическое отклонение по эксцессу.
При этом и зависят от одного фактора – числа данных (n) и представляют собой стандартные ошибки.
Для определения таких значений используется правило 3σ:
|
-
|
≤ 3σ
Суть закона: значение принадлежит выборке, если отклонение значения фактора от среднего арифметического по модулю не превышает утроенного среднеквадратического отклонения.
Все опыты либо наблюдения содержащие ошибки в векторе-столбце исключается из выборки.
В рассматриваемой группе изначально было 153 хозяйства, после проверки информации их осталось 131 (удалено 22 наблюдения). (Приложение 1). Дальнейшая проверка оставшихся данных после удаления показала, что А и Э удовлетворяет условиям допустимости (Приложение 2).
Итак, нам необходимо построить линейную корреляционную модель, которая будет иметь вид:
При
построении регрессии нашли неизвестные
коэффициенты и, подставив в уравнение,
получили:
(Приложение 3).