Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рязанский Государственный Университет им. С.А. Есенина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лабораторная работа4.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

1.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

По формуле вычислим значение статистики

Это значение не принадлежит критической области, поэтому оснований отвергать гипотезу Н₀: ₁² = ₂² нет, т.е. считаем дисперсии генеральных совокупностей равными.

Пример 6. Для непрерывных случайных величин х₁ и х₂ известны выборочные характеристики: .

Решение.

Сначала проверяем гипотезу о равенстве дисперсий.

Задано:  = 0,01.

Проверить: Н₀: ₁² = ₂² при Н₁: ₁² > ₂² .

Получаем следующую критическую область:

P(F > f_) = 0,01, f_ = 2,92, F > 2,92.

Значение статистики

не принадлежит критической области, поэтому принимаем гипотезу Н₀о равенстве дисперсий. Следовательно, стоит проверить и гипотезу о равенстве средних значений генеральных совокупностей.

Задано:  = 0,01.

Проверить: Н₀:  = 0 при Н₁:  > 0.

Получаем следующую критическую область:

P(t > t_) = 0,01, t_ = 2,42.

Значение статистики

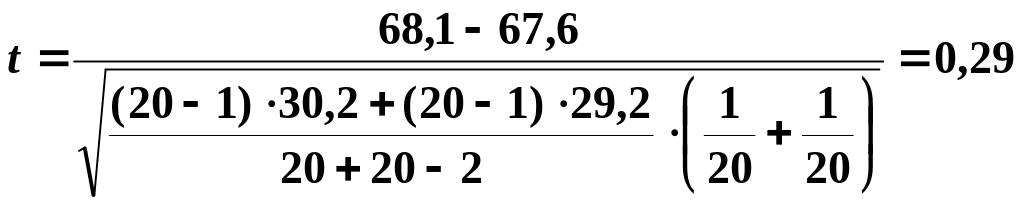
не принадлежит критической области, поэтому принимаем гипотезу Н₀о равенстве средних значений.

Варианты заданий

1. По выборке Х (в таблице выбрать строки с № варианта) при уровне значимости  проверить гипотезу о среднем значении Н₀:  = М при альтернативной гипотезе Н₁:   М, если задано стандартное отклонение .

Имеем

 = 0,01 + k/100, k =остаток (V/10),  = 8,

№ варианта		1	2	3	4	5	6	7	8	9	10	11
1		67	68	70	76	80	87	75	79	79	73	86
2		48	40	52	50	39	47	38	46	47	44	45
3		46	55	57	55	51	62	43	64	56	65	56
4		31	28	30	23	25	25	25	27	31	25	28
5		77	76	62	83	83	79	77	81	71	83	73

№ варианта	12	13	14	15	16	17	18	19	20	21	22
1	78	79	67	79	-	-	-	-	-	-	-
2	44	53	52	45	42	45	45	-	-	-	-
3	51	58	42	46	54	62	57	68	47	69	65
4	25	30	28	28	31	-	-	-	-	-	-
5	81	82	77	82	83	80	77	69	78	-	-

2. По выборке Y (в таблице выбрать строки с № варианта) при уровне значимости  проверить гипотезу о среднем значении Н₀:  = М при альтернативной гипотезе Н₁:   М, если  неизвестно.

Имеем: k = остаток (V/5)

№ варианта	1	2	3	4	5	6	7	8	9	10	11
6	23	38	34	16	42	44	33	18	29	42	39
7	71	62	91	60	79	85	79	54	71	67	90
8	117	103	108	102	91	110	111	111	109	96	96
9	96	86	96	68	92	54	81	89	78	71	77
10	152	152	155	144	145	155	154	136	142	147	153

№ варианта	12	13	14	15	16	17	18	19	20	21	22
6	36	27	30	36	31	38	35	45	48	18	30
7	81	61	54	77	82	72	91	81	-	-	-
8	108	97	108	102	109	-	-	-	-	-	-
9	79	81	81	66	85	92	68	104	83	81	92
10	145	143	168	143	134	152	139	141	146	146	142

3. По выборке Z (в таблице выбрать строки с № варианта) при уровне значимости  проверить гипотезу о дисперсии Н₀: ² = Т при альтернативной гипотезе Н₁: ²Т.

Имеем:

k = остаток (V/4)

№ варианта	1	2	3	4	5	6	7	8	9	10	11
11	82	70	83	80	76	81	80	76	70	79	74
12	61	42	55	52	44	41	47	43	55	43	49
13	59	57	48	41	57	50	64	43	57	54	50
14	75	68	65	80	71	61	77	69	64	68	52
15	23	28	26	26	28	27	25	26	27	28	27

№ варианта	12	13	14	15	16	17	18	19	20	21	22
11	77	65	80	79	-	-	-	-	-	-	-
12	42	31	40	47	43	48	44	-	-	-	-
13	59	48	45	51	40	59	46	47	55	49	64
14	59	63	56	62	67	-	-	-	-	-	-
15	29	24	23	27	27	-	-	-	-	-	-

4. По выборкам X₁ и X₂ (в таблице выбрать строки с № варианта) при уровне значимости  проверить гипотезу о равенстве средних значении Н₀: = 0 при альтернативной гипотезе Н₁:  0, если неизвестные дисперсии обеих совокупностей считать равными.

Имеем

k =остаток (V/5),

№ варианта	1	2	3	4	5	6	7	8	9	10	11
16	52	49	45	44	34	-	-	-	-	-	-
16	36	42	48	37	37	-	-	-	-	-	-
17	48	33	53	43	38	47	-	-	-	-	-
17	45	41	49	42	43	41	-	-	-	-	-
18	114	96	113	98	-	-	-	-	-	-	-
18	106	107	99	95	-	-	-	-	-	-	-
19	-20	-28	-4	-11	-20	-26	-24	-	-	-	-
19	-8	-7	-19	-26	-11	-11	-15	-	-	-	-
20	46	49	48	47	45	48	-	-	-	-	-
20	45	43	43	42	48	44	-	-	-	-	-

5. По выборкам X₁ и X₂ (в таблице выбрать строки с № варианта) при уровне значимости  проверить гипотезу о равенстве дисперсий Н₀: ₁²= ₂² при альтернативной гипотезе Н₁: ₁²> ₂² .

Имеем

№ варианта	1	2	3	4	5	6	7	8	9	10	11
21	49	43	47	43	46	45
21	45	46	46	44	43	45
22	-22	-25	-22	-42	-24	-30	-29
22	-22	-24	-14	-25	-17	-27	-21
23	114	105	103	122	118	113	107
23	120	113	109	111	102	116	113
24	-17	-15	-15	-14	-18
24	-16	-8	-20	-17	-14
25	50	51	51	51	46
25	46	49	51	49	56

6. По выборкам X₁ и X₂ (в таблице выбрать строки с № варианта) при уровне значимости  проверить сначала гипотезу о равенстве дисперсий и, если она принимается, то затем гипотезу о равенстве средних значений.

Получаем

№ варианта	1	2	3	4	5	6	7	8	9	10	11
26	90	83	81	83	86	87	90	85	99	91	92
26	92	79	82	103	93	89	93	91	83	104	95
27	16	16	16	13	16	10	16	15	14	13	12
27	13	16	15	17	15	16	17	17	16	12	13
28	39	36	35	20	31	41	24	22	38	35	26
28	34	31	34	36	19	34	28	30	24	17	27
29	89	89	89	90	89	90	91	88	89	90	89
29	89	91	88	90	91	90	88	89	89	90	89
30	32	40	36	40	36	34	33	35	36	43	29
30	40	39	28	39	28	32	40	37	30	32	34

№ варианта	12	13	14	15	16	17	18	19	20	21	22
26	98	87	89	108	82	79	93	91	98	90	-
26	97	100	92	92	84	93	98	97	104	84	-
27	13	15	14	13	14	17	13	18	15	13	17
27	13	14	12	14	16	13	19	14	17	13	16
28	34	16	35	22	-	-	-	-	-	-	-
28	29	33	32	30	-	-	-	-	-	-	-
29	90	89	89	-	-	-	-	-	-	-	-
29	91	89	90	-	-	-	-	-	-	-	-
30	41	44	36	37	-	-	-	-	-	-	-
30	40	40	36	36	-	-	-	-	-	-	-

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025198.14 Кб0лаб_работа_ №_1_МАИ.doc
#
13.02.2015231.94 Кб18Лабораторная 3.2.doc
#
10.08.201926.49 Кб13Лабораторная работа №15.docx
#
01.04.2025393.22 Кб0Лабораторная работа2.doc
#
01.04.2025203.78 Кб0Лабораторная работа3 с контрольными вопросами.doc
#
01.05.20251.83 Mб0Лабораторная работа4.doc
#
01.05.2025779.26 Кб1Лабораторная работа5.doc
#
18.11.2019303.1 Кб11ЛАБОРАТОРНОЕ ЗАНЯТИЕ.doc
#
01.05.2025291.33 Кб2Лабораторные работы 2013 г.doc
#
13.02.2015134.66 Кб12Лабораторный практикум ИСИКТУП.doc
#
13.02.20151.47 Mб271Лабораторный практикум по неорганической химии.pdf