2.2.Теория ожидаемой полезности
Теперь пусть одним из товаров являются деньги. Тогда подобный вариант обмена товара есть покупка товара одним из участников у другого участника и эта сделка обоюдовыгодна.
С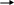
истема
предпочтений индивида указывает, какой
из двух наборов предпочтительнее для
него. Во многих случаях, однако, весьма
желательно и удобно оценивать
привлекательность набора товаров
количественно, т.е. приписать каждому
набору Х
из пространства товаров С
какое-то
число (Х).
Получается функция и:
С R.
Главное требование к такой функции –
она должна отражать отношение (слабого)
предпочтения на С, т.е.
u (Х)< u (Y), если и только если Х < Y
u (X) =u (Y), если и только если Х~ Y, значит и
u (X)< u (Y), если и только если Х< Y.
Такая функция u (Х) называется функцией полезности. Работать с функцией полезности гораздо удобнее, чем с системой предпочтения.
2.3.Отношение инвестора к риску. Полезность денег
Хорошо известно разное отношение людей к деньгам. Обозначим
d(x) – полезность денежной суммы для индивида. Тогда примерный график d(x) показан на рис.3.
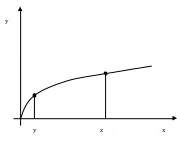
Рис. 4. Функция полезности денег
Самое важное свойство этой функции – её вогнутость, т.е.
d (z+y) < d (z) + d (y) для любых сумм z, y, или, другими словами: отрезок, соединяющий две точки графика функции, лежит ниже этого графика. Можно сформулировать это свойство и так: прирост полезности денег уменьшается с увеличением их количества. Это утверждение ниоткуда не следует, однако подтверждается всей человеческой практикой и поэтому его надо рассматривать, как аксиому, характеризующую поведение индивидуума.
Если функция d(x) дифференцируема, то из того, что полезность денег увеличивается с ростом их количества, следует, что d’(x)>0, а сформулированная аксиома влечёт, что d”(x)<0.
Теория полезности существует в двух видах: теория предпочтений индивида и отражающая ее функция полезности – это детерминированный вариант, и теория ожидаемой полезности – стохастический вариант, основы которого были заложены Д. Бернулли в 1783 г., раньше, чем детерминированной.
Понятие полезности оказало решающее влияние на психологию и философию, потому что Бернулли предложил стандарт для оценки разумности человеческого поведения. Например, люди, для которых полезность богатства растет вместе с его ростом, считаются большинством психологов и моралистов невротиками.
Теория полезности требует от разумного человека способности оценивать полезность при любых обстоятельствах и, руководствуясь этой оценкой, делать выбор и принимать соответствующие решения – высокая планка, если учесть, что нам всю жизнь приходится действовать в условиях неопределенности. У каждого своя информация, и к тому же каждый склонен окрашивать ее по-своему. Даже самые разумные люди часто не могут договориться о том, что значат те или иные факты.
Поведение индивида предполагается рациональным и описывается в простейших ситуациях максимизацией ожидаемого значения функции полезности, например, дохода.
Будем исходить из упрощенного понятия полезности, в соответствии с которым все побуждения представительного инвестора (ЛПР) описываются одной числовой величиной – доходом, и чем больше доход, тем больше его полезность. Таким образом, полезность рассматривается как неубывающая функция и(е) с единственной переменной – доходом е; примем, что и(0) =0.
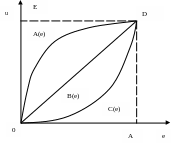
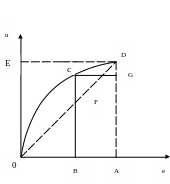
Теоретически могут существовать три типа возрастания функции и(е): с затухающими, неизменными и нарастающими приростами полезности и при движении аргумента по оси дохода с одинаковым шагом r. Этим возможностям отвечают варианты графиков, изображенных на рис. 5 (а,б,в,г).
При сравнении кривых просматривается разница между б), в), г) в смысле оценок повышения полезности от выигрыша некоторой суммы (ВА) по сравнению с потерей той же суммы (ВО=ВА).
Так для б) – при одинаковых выигрышах и потерях последние воспринимаются более ощутимо (GD<BC), в случае в) – оценки приобретений и потерь равнозначны и в случае г) – более ощутимы выигрыши (GD>BC).
Отсюда понятно, что экономическое поведение по типу б), при котором человек больше боится потерять, чем желает приобрести, будет отличаться от типов в) и г) в пользу осторожных решений и умеренных действий. Этого почти достаточно, чтобы классифицировать кривую б) как полезность для несклонных к риску предпринимателей.
Реальный опыт, основанный, в частности, на многочисленных специальных экспериментах, убеждает, что большинство субъектов экономики (индивидуумы, фирмы, инвесторы и т.п.) в своих действиях и решениях склонны к стабильности.
В пользу такого вывода говорит, например, более высокий уровень ожидаемой эффективности рисковых вложений по сравнению с безрисковыми. При игнорировании риска вложения потекли бы к более эффективным, но менее надежным активам. В результате возросшего спроса на рисковые инвестиции их ожидаемые доходности поползли бы вниз до уровня эффективности безрисковых вложений.
Следовательно, с полным основанием можно сказать, что наиболее адекватно поведение инвестора описывает графическая модель б), изображенная на рис.5 Эту выпуклую функцию называют функцией уклонения от риска, а линейную и вогнутую функции (рис. в) и г)) – соответственно нейтральной относительно риска и функцией стремления к риску.
Примерами функций полезности являются квадратическая и=а+be-ce2, логарифмическая и=lne, логарифмическая со сдвигом и=ln(1+ae), экспоненциальная и=1-е-ае, степенная и=еа, где 0<а<1.
Однако эти функции зависят только от дохода е и поэтому не учитывают влияния внешних факторов на предпочтения ЛПР и, следовательно, на вид кривых полезности.
б) с падающей отдачей а)общая схема
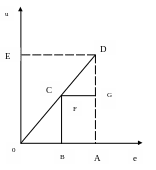
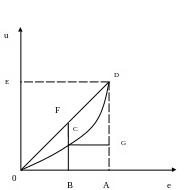
в)с постоянной отдачей г)с возрастающей отдачей
Рис.5