Тема 5. Модель оценки доходности финансовых активов (сарм)

Рисковость портфеля, измеряемая средним квадратическим отклонением доходности, как правило, меньше средней величины рисков отдельных активов, входящих в портфель. Это имеет большое значение при определении требуемой доходности ценной бумаги. Инвесторам выгоднее владеть портфелем ценных бумаг, а не отдельной ценной бумагой. Поэтому есть все основания для оценки рисковости любой ценной бумаги не при рассмотрении ее изолированно, а с точки зрения ее вклада в рисковость портфеля.

Модель САРМ (Capital Asset Pricing Model), устанавливает связь между риском и требуемой доходностью активов, представляющих хорошо ди­версифицированный портфель.

Модель САРМ была разработана Уильямом Ф. Шарпом и впервые опубликована в 1964г. Он лауреат Нобелевской премии по экономике за исследования в области ценообразования финансовых активов.

Как и во всех финансовых теориях, в основу САРМ положен целый ряд допущений, включая, в том числе, наличие идеального рынка капитала. Некоторые из них следующие.

1. Основной целью каждого инвестора является максимизация возможного прироста своего достояния на конец планируемого периода путем оценки ожидаемых значений доходности и средних квадратических отклонений альтернативных инвестиционных портфелей.

2. Все инвесторы могут брать и давать ссуды неограниченного размера по некой безрисковой процентной ставке k_RF.

3. Все инвесторы одинаково оценивают величину ожидаемых значений, дисперсии и ковариации доходности всех активов; это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей.

4. Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут быть проданы на рынке по существующей цене).

5. Не принимаются во внимание налоги.

6. Все инвесторы принимают цену как экзогенно заданную величину (т. е. все инвесторы предполагают, что их деятельность по покупке и продаже ценных бумаг не оказывает влияния на уровень их цен).

7.Количество всех финансовых активов заранее определено и фиксировано.

5.1.Линия рынка капитала (cml)

На рис.9 построен график для случая n числа активов и добавлен безрисковый актив с доходностью k_RF. Безрисковый актив, по определению, имеет нулевой риск, и, следовательно, его = 0, поэтому он может быть изображен точкой на вертикальной оси.

Рис.9 показывает возможное множество рисковых активов (заштрихованная область) и совокупность кривых безразличия (I₁ – I₃), отображающих выбор между риском и ожидаемой доходностью для отдельного инвестора. Точка N , в которой кривая безразличия I₁ является касательной к эффективному множеству, отражает выбор возможного портфеля. Это точка на эффективной границе множества рисковых портфелей, в которой инвестор получает самую высокую возможную доходность при данной величине риска , и наименьшую величину риска при данной ожидаемой доходности . Однако инвестор может сделать лучший выбор, чем портфель N; он может достичь более высокой кривой безразличия. Для этого в портфель рискованных активов добавляется безрисковый актив. Благодаря этому можно достичь любой комбинации риска и доходности на прямой линии, соединяющей k_RF с М - точкой касания прямой линии и границы эффективного множества портфелей акций.

Портфель, изображаемый точкой на линии k_RFMZ, будет предпочтительней любого рискового портфеля, изображаемого точкой на границе эффективности ВNМЕ, поэтому точки на линии k_RFMZ представляют собой наилучшие достижимые комбинации риска и доходности.

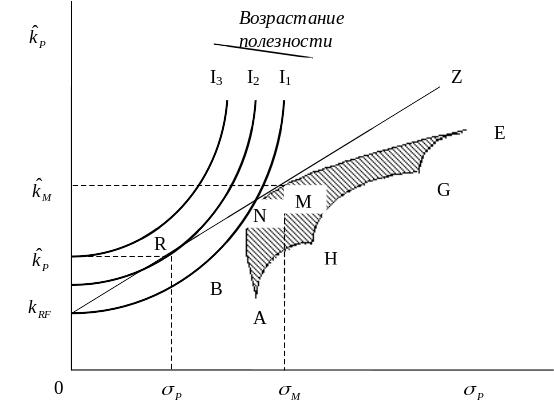
Рис. 9.Комбинирование безрискового актива с рыночным портфелем

Имея новое множество возможностей k_RFMZ, инвестор перейдет из точки N в точку R, которая находится на более высокой достижимой кривой безразличия риск/доходность. Любой точке на предыдущей эффективной границе ВNМЕ (кроме точки касания М) следует предпочесть точки, лежащие на линии k_RFMZ . Возможность перехода в некую точку R на более высоком уровне как раз и объясняется комбинированием безрисковой ценной бумаги и рискового портфеля М.

Поскольку инвестор может получать необходимый ему кредит, а также предоставлять свои ресурсы в долг, а это эквивалентно покупке безрисковых долговых ценных бумаг по безрисковой ставке k_RF, существует возможность выхода на линейный отрезок MZ, что и происходит, если кривая безразличия инвестора касается k_RFMZ в точке М.Все инвесторы при условии соблюдения предпосылок САРМ должны иметь портфели, обозначенные точками, лежащими на линии k_RFMZ.. Таким образом, добавление безрисковой акции ведет к изменению эффективного множества: оно теперь лежит вдоль линии k_RFMZ, а не вдоль кривой ВNМЕ

Если рынок капитала находится в равновесии, то М должно быть таким портфелем, в который любой рисковый актив включается пропорционально доле этого актива в общей рыночной стоимости всех активов; т. е. если доля ценной бумаги составляет х% общей рыночной стоимости всех ценных бумаг, то х% рыночного портфеля должно приходиться на ценную бумагу .

Таким образом, все инвесторы должны владеть портфелями, изображенными точками на линии k_RFMZ, а точное расположение данного портфеля определяется точкой, в которой кривая безразличия инвестора касается этой линии.

Линия k_RFMZ на рис.8 называется линией рынка капитала (СМL). Она пересекается с вертикальной осью в точке, соответствующей k_RF, а ее наклон равен . Поэтому уравнение линии рынка капитала может быть записано следующим образом:

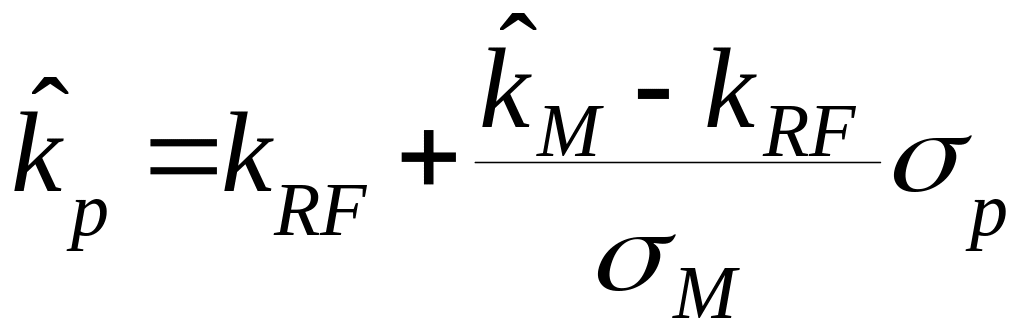. (5.1)

Уравнение (5.1) показывает, что ожидаемая доходность эффективного портфеля (т.е. портфеля, лежащего на линии CML) равна сумме безрисковой ставки и премии за риск, исчисляемой умножением на среднее квадратическое отклонение портфеля, . Таким образом, CML устанавливает линейную зависимость между ожидаемой доходностью и риском. Наклон CML определяется разностью между ожидаемой доходностью рыночного портфеля рисковых акций и безрисковой доходностью k_RF (эта разность называется премией за рыночный риск), деленной на среднее квадратическое отклонение доходности портфеля, :

.

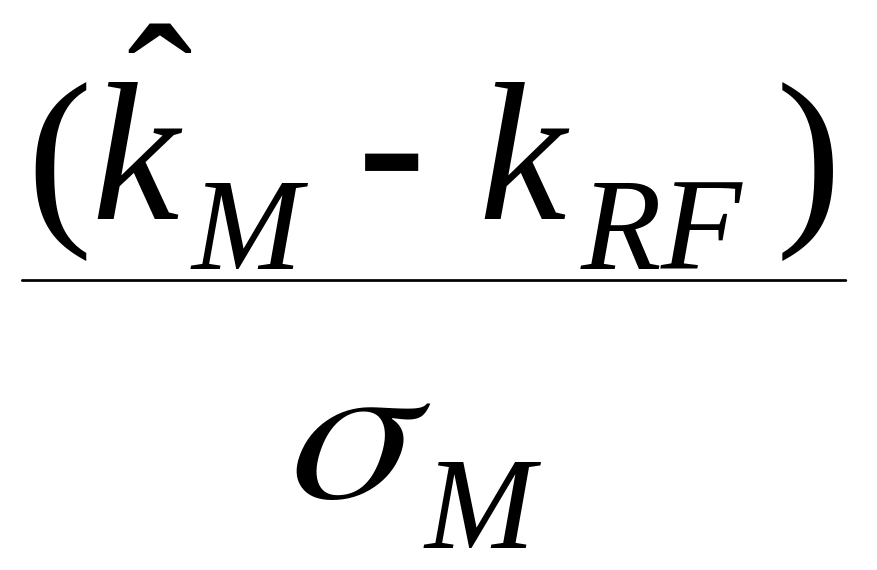Например, если k_RF = 10%, а = 15% и = 15%. Тогда CML будет равен (15%—10%) : 15% = 0.33, и если портфель имеет =10%, то

=10% + 0.33*10% = 13.3%.

А

рисковый портфель с = 20% будет иметь = 10% + 0.33(20%) = 16.6%.