7.2. Композиционные материалы, армированные короткими волокнами

КМ с короткими волокнами занимают промежуточное положение между материалами с дисперсным наполнителем и с непрерывными волокнами.

Одним из способов разделения КМ на три класса – с дисперсными частицами, короткими и непрерывными волокнами – является отношение наибольшего и наименьшего размеров частиц наполнителя, то есть его характеристического отношения.

У КМ с дисперсными частицами отношение l/d  1 с непрерывными волокнами – равно бесконечности, с короткими - от 10 до 1000.

Дисперсные наполнители практически не могут оказывать первичного усиливающего эффекта, так как только очень малая доля прикладываемого к матрице напряжения может быть передана на частицу, а разрушение происходит или по границе раздела или по матрице, при условии, что частицы наполнителя прочнее матрицы. Но при этом может наблюдаться вторичный усиливающий эффект, если частица наполнителя жестче матрицы, что чаще всего и наблюдается, то они могут препятствовать поперечному сжатию матрицы, как упругому, так и пластичному, в результате чего возникающее объемно-напряженное состояние повышает уровень разрушающего напряжения при растяжении.

Для КМ на основе бесконечных волокон можно предположить, что волокно и матрица деформируются одинаково, а прикладываемое напряжение делится между двумя фазами пропорционально их относительным площадям поперечного сечения и модулем упругости. В этом случае введение высокопрочных волокон увеличивает прочность КМ в целом.

В КМ с короткими волокнами напряжение, прикладываемое к матрице, может частично передаваться на волокно при условии высокой адгезионной прочности наполнителя и матрицы или высокого трения на границе раздела волокно-матрица. Концы волокна не могут быть нагружены, так как матрица не может передавать напряжения на них.

При удалении от концов волокна силы межфазного трения или сдвиговое напряжение могут распространяться на все большую площадь. При этом растягивающие напряжения на волокне будут все больше возрастать, пока они, если волокно имеет достаточно большую длину, не достигнут уровня, аналогичного напряжению на непрерывном волокне. Одновременно сдвиговые напряжения на границе раздела волокно-матрица постепенно убывают при удалении от концов волокна, пока деформации при растяжении волокна и матрицы не выравниваются, как в КМ с непрерывными волокнами, рис. 7.

Рис. 7. Схема распределения растягивающих напряжений G и напряжений сдвига  вдоль короткого волокна, находящегося в матрице:

1-матрица; 2-волокно; Р-приложенная нагрузка; l –длина волокна

Наклон прямой возрастания растягивающего напряжения зависит от адгезии между волокнами и матрицей и их упругих свойств.

При конструировании однонаправленных КМ, растягиваемых вдоль волокон, необходимым условием использования механических свойств волокон является условие l  l_кр, то есть фактическая длина волокон должна быть не меньше критической длины l_кр.

Под критической длиной армирующих волокон в однонаправленном КМ принимают их минимальную длину, при которой касательные напряжения на границе раздела с матрицей, передающей нагрузки на волокна, достаточны для реализации прочности волокон [12]. Известно, что прочность КМ, армированных короткими волокнами, но с ll_кр, не меньше прочности материалов, наполненных непрерывными волокнами. Это связано с тем, что у армирующих непрерывных волокон имеются дефекты (трещины, изломы). КМ на их основе стабильны только в том случае, если расстояние между дефектами  l _кр.

Эффективность волокон в КМ возрастает с увеличением l_кр и при l=l_кр напряжение, воспринимаемое собственно волокном в материале, становится равным прочности волокна G_(р)в. При разрушении КМ, наполненного волокном, наблюдается выдергивание коротких волокон из полимерной матрицы, то есть материал разрушается по границе волокно-матрица. Волокна с ll_кр сами разрушаются и полностью реализуют всю прочность в полимерной матрице [4,21].

Значение l_кр рассчитывается по формулам:

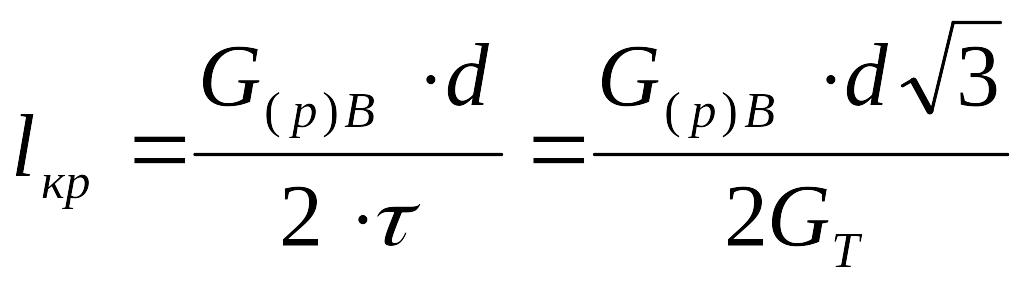или ,

где d – диаметр волокна;  - напряжение сдвига на границе волокно-матрица; φ_в – содержание волокна; Е_в – модуль упругости волокна; G_т и Е_сд – предел текучести и модуль сдвига матрицы соответственно.

Критическая длина волокон зависит от их природы: для углеродного волокна – 100 мкм; для стеклянного – 400 мкм.

Значения l_кр (в мм) стеклянных волокон d  10 мкм для различных полимерных матриц следующие [4]: ПЭ – 1,8; ПП– 0,6; ПС – 0,36; ПА – 0,26; эпоксидной смолы – 0,15. Чем меньше l_кр волокна, тем эффективнее волокно с ll_кр упрочняет полимерную матрицу. Теоретически показано, что при l10l_кр волокно в полимере воспринимает на себя до 90% внешней нагрузки, на практике l = 100l_кр. Увеличение длины волокна l_кр приводит к упрочнению полимеров, однако одновременно с этим уменьшается max, возрастает вязкость наполненных материалов, ухудшается перерабатываемость и изменяется метод формования изделий.

В связи с этим выбор длины волокон требует оптимизационного подхода. Волокна длиной 312 мм используют для получения конструкционных литьевых и экструзионных термопластичных материалов; длиной менее 1-2 мм - заливочных отверждающихся компаундов с малой усадкой; длиной от 15 до 70 мм - пресс-материалов (волокнитов и премиксов на основе фенолоформальдегидных и полиэфирных смол.

При расчете прочности КМ, армированных короткими волокнами, возможны следующие два случая:

1. Если ll_кр, то волокна могут быть нагружены до разрушения. Однако среднее напряжение в волокне G_вG_в и зависит от распределения напряжений на концах волокна. Если предположить, что растягивающее напряжение в волокне возрастает от конца волокна по линейной зависимости, то среднее разрушающее напряжение для волокна

,

,

где l –длина волокна,

2. Если l  l_кр, то , а поскольку эффективное напряжение равно половине максимального, то

,

где _м - разрушающее напряжение при сдвиге на границе раздела волокно- матрица.

В КМ с короткими волокнами трудно добиться одноосной ориентации волокон. Хаотическое распределение волокон резко снижает эффект усиления. Одним из путей учета относительной эффективности усиления волокнами является использование коэффициентов эффективности – коэффициентов Кренчеля [22]:

,

где  - коэффициент Кренчеля; Ф – коэффициент, учитывающий распределение напряжений на концах волокон (рис.8).

Для расчета модуля упругости КМ, наполненных короткими волокнами, используются формулы:

1. при llкр ;

2. при llкр ,

где Е_КМ, Е_В и Е_М – модули упругости КМ, волокна и полимера соответственно.

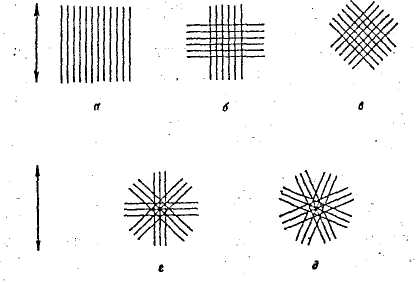
Рис. 8. Коэффициенты эффективности усиления волокнистых КМ

с различным распределением волокон:

а – χ =1; б – χ ½; в- χ=3/8; д – χ=3/8 – для однородного статистического распределения в плоскости; для однородного статистического объемного распределения χ=1/6.

Стрелки указывают направление прикладываемого напряжения

Прочность при сжатии. КМ, армированные короткими волокнами, изотропны, волокна в них распределены хаотично. Прочность таких материалов при растяжении и сжатии примерно одинакова. Если волокна ориентированы в направлении сжатия, то разрушение при сжатии наступает при меньшем напряжении, чем при растяжении. В КМ с низкой адгезионной прочностью при сжатии возможно продольное проскальзывание волокон, тогда как при растяжении поперечные силы, возникающие вследствие эффекта Пуассона, увеличивают прочность сцепления волокна с матрицей и поэтому G_рG_сж, При сжатии композиций с высокой адгезией наполнителя со связующим может быть реализована значительная часть их прочности при растяжении, однако при сжатии большую часть нагрузки выдерживает матрица, а так как волокна не непрерывны, то локальные сдвиговые разрушения в матрице способствуют разрушению волокон при продольном изгибе с разрушением границы раздела волокон с матрицей и потерей усиливающего эффекта волокон.

Прочность при сдвиге. В отличие от КМ с непрерывными волокнами, имеющими низкую сдвиговую прочность в плоскостях, параллельных плоскости ориентации волокон, материалы с короткими, даже хорошо ориентированными волокнами, всегда имеют большое число волокон, расположенных под некоторым углом к направлению ориентации. Эти волокна затрудняют сдвиговые деформации в плоскости ориентации и увеличивают G_сд. Они также увеличивают трансверсальную прочность материала при растяжении и уменьшают возможность смещения волокон вдоль растягивающих усилий.