4. Деформационно-прочностные свойства наполненных материалов

Механические свойства полимеров - комплекс свойств, определяющих поведение материалов при действии на них различно приложенных внешних сил. При воздействии внешних сил полимерные материалы деформируются, а при значительных и длительных воздействиях разрушаются. Поэтому полимеры характеризуют деформационными и прочностными свойствами. Деформация – изменение структуры, объема и линейных размеров тела под давлением внешних сил. Прочность - это устойчивость твердого тела к действию внешних сил без изменения формы и разрушения, характеризующаяся пределом прочности, то есть величиной напряжения, при которой еще не происходит разрушение материала в условиях нагружения. Предельные возможности материала противостоять воздействию внешних сил характеризуются напряжением, соответствующим разрушению образцов (изделий).

Долговечность – это продолжительность от момента приложения нагрузки до момента разрушения материала. Зависит от структуры материала, внутренних напряжений, а также от величины приложенных нагрузок и температуры испытания. Существенно влияют на долговечность технология переработки и последующей обработки изделий и условия эксплуатации.

При введении наполнителей изменяются многие свойства композиционных материалов.

Разнообразие природы, структуры наполнителей и их различные сочетания позволяют создать огромное количество марок материалов на основе термопластичных и термореактивных матриц со специальными свойствами: электроизоляционные, электропроводные, магнитодиэлектрики, тепло- и звукоизоляционные, фрикционные и антифрикционные, ударопрочные, влаго- и химически стойкие, негорючие и т.д., например:

Материалы	Наполнители
Электроизоляционные	Слюда, тальк, молотый кварц, асбест, карбонат кальция, оксид алюминия, стекловолокно.
Антифрикционные	Графит, дисульфид молибдена, нитрат бора, фторопласт.
Тепло-, жаростойкие	Асбест, кокс, графит, углеродные волокна.
Химически стойкие	Графит, фторопласт, технический
	углерод, асбест, тальк.
Тепло-, электропроводные	Графит, технический углерод, углеродные волокна, порошки металлов.

Модуль упругости, как мера жесткости материала, характеризует сопротивление развитию обратимых деформаций. В технике жесткость является важным параметром, поэтому необходимо точно знать деформации, отклонения или перемещения, происходящие в конструкции и ее отдельных элементах под действием внешних сил. При действии нагрузок между элементами конструкций должны сохраняться точное соответствие и необходимые зазоры. Например, при действии нагрузок на самолет двери не должны заклиниваться, а крылья сильно деформироваться. Введение жестких частиц наполнителя приводит к увеличению модуля упругости, а мягких, эластичных – к снижению [10].

Для расчета модуля упругости дисперсно-наполненных полимеров принимают обобщенное уравнение Нилсена-Кернера:

или ,

где

; ; ;

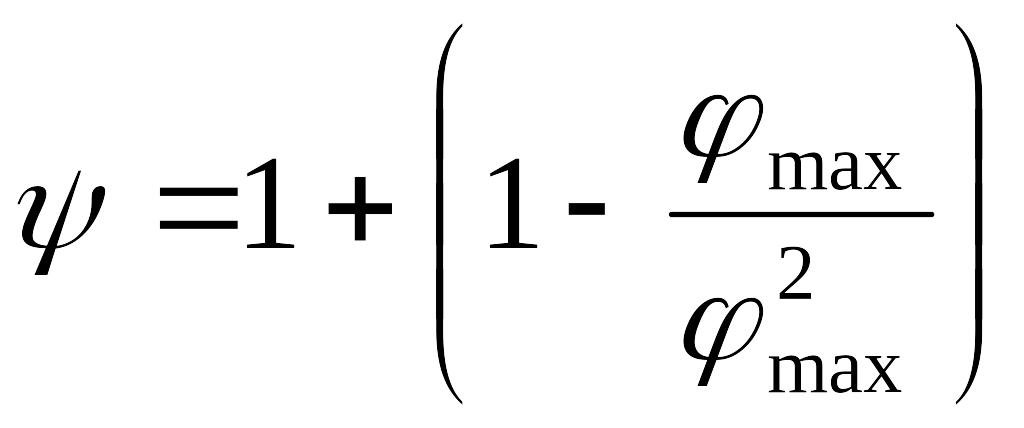Е_км , Е_м и Е_н - модули упругости (сжатия, растяжения, изгиба) композиционного материала, матрицы и наполнителя; м - коэффициент Пуассона матрицы; _н и _max - объемная и максимальная объемная доли наполнителя, соответственно.

Относительное удлинение при разрыве наполненного материала определяется конкретным механизмом его разрушения [4]. Теория этого явления довольно сложна, однако при хорошей адгезии можно с достаточной точностью рассчитать удлинение при разрыве в зависимости от содержания твердого наполнителя:

,

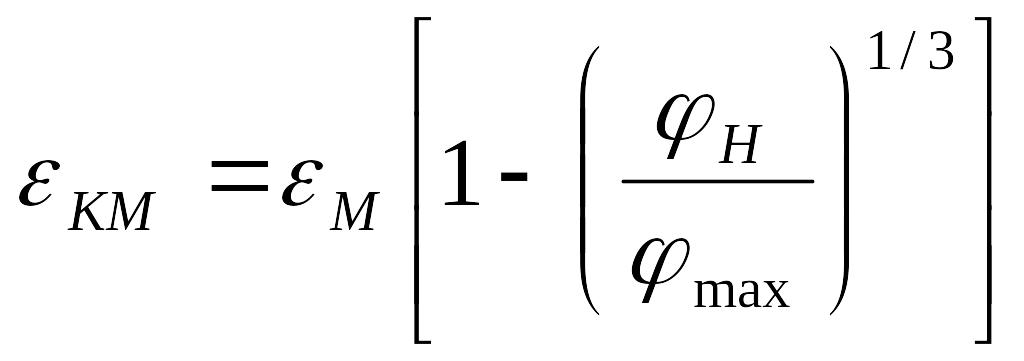где _км и _м - деформация наполненной и ненаполненной матрицы.