4.5.4. Линеаризация моделей

Линеаризация исходной нелинейной модели облегчает решение конкретной задачи исследования. Поэтому для упрощения моделирования и исследования, когда это возможно, желательно заменить нелинейное уравнение приближенным линейным, решение которого с достаточной степенью точности описывает свойство исходной нелинейной системы. Процесс замены нелинейной модели линейной называется линеаризацией [19,48].

Если дифференциальное уравнение объекта нелинейно из-за нелинейности его статической характеристики, то для линеаризации уравнения необходимо заменить нелинейную статическую характеристику.

Основное содержание идеи линеаризации состоит в том, что различие в решениях нелинейных уравнений и их линеаризованного представления не столь существенны, чтобы приводить к недопустимым ошибкам в смысле требований к точности решения поставленной задачи. Для линеаризации нелинейной модели системы управления

(4.42)

чаще всего применяют метод малых отклонений.

Техника составления линеаризованных уравнений принципиально проста. Математическое обоснование этой процедуры заключается в требованиях к виду нелинейности функции . Для допустимости линеаризации достаточно, что , и существуют и непрерывны в некоторой окрестности точки (x₀, y₀, u₀). Тогда линеаризация осуществляется при помощи разложения в ряд Тейлора функции в окрестности точки (x₀, y₀, u₀) и отбрасыванием всех нелинейных членов этого ряда. Интуитивно ясно, что линеаризованная модель, полученная при помощи разложения в ряд Тейлора, может оказаться пригодной для описания процессов в нелинейном объекте, не связанных с большими изменениями переменных в окрестности точки (x₀, y₀). Ошибка моделирования тем меньше, чем меньше отклонения переменных.

Таким образом, идея линеаризация нелинейных моделей состоит в том, что вместо (4.42) используют упрощенные математические модели, основанные на том, что процессы в системе протекают, мало отклоняясь от некоторой так называемой опорной траектории (x₀, u₀, y₀), удовлетворяющей уравнениям:

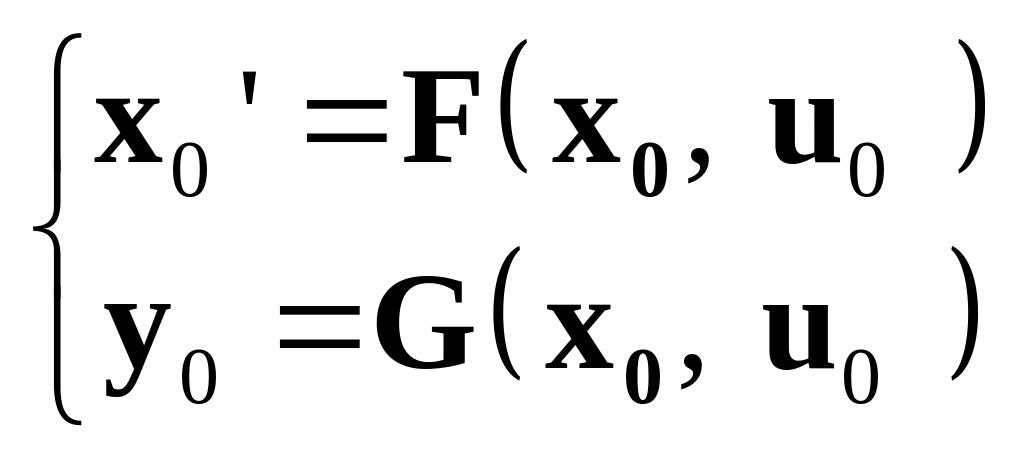. (4.43)

Тогда можно записать приближенную линеаризованную модель в отклонениях от этого режима:

, (4.44)

Пример 1.1. Линеаризовать уравнение состояния .

Решение. Линеаризуем уравнение состояния вблизи траектории, соответствующей . Имеем , откуда решая это уравнение, получаем, что либо (при ), либо .

Рассмотрим второй случай (так как первый тривиален):

.

.

В отклонениях ,  линеаризованное уравнение имеет вид:

. (4.45)

Если расчетный режим является установившимся, т.е. не зависит от времени, то коэффициенты в (4.44) также не зависят от времени. Такие системы называются стационарными. Особенно часто на практике встречаются стационарные линейные непрерывные системы, описываемые уравнениями:

, .

Если линеаризация приводит к большим погрешностям, то надо выбрать модель, линейную по параметрам:

,

где a − матрица порядка nN;  − нелинейная вектор-функция.

К этому классу относятся, к примеру, билинейные объекты:

x'=a₁x+a₂xu+a₃u, где a=(a₁, a₂, a₃), =(x, xu, u).

Сказанное относится и к дискретных по времени систем.