4.5. Методы упрощения моделей

4.5.1. Общие подходы к упрощению моделей

Когда полученная математическая модель является сложной, т.е. неразрешимой, разработчик прибегает к ее упрощению и использованию более глубокой абстракции. В практических задачах исследования процессов функционирования сложных систем часто желателен обратный процесс − процесс расширения модели. При этом начинают с построения простой модели, а затем усложняют ее. Эволюционный характер процесса конструирования модели упрощает решение поставленной задачи. Сначала решаются более простые задачи с помощью простой модели, а затем ставятся более сложные задачи, что требуют достижения большего соответствия между моделью и реальным объектом, что приводит к усложнению модели. В обоих случаях возникает необходимость упрощения математических моделей объекта.

Наиболее распространенными являются следующие методы упрощения моделей:

• расчленение сложной системы на ряд более простых подсистем (декомпозиция);

• выделение существенных свойств и воздействий и учет остальных в параметрической форме (метод макромоделирования);

• линеаризация нелинейных процессов в некоторой области изменения переменных;

• приведение систем с распределенными параметрами к системам c сосредоточенными параметрами (введение более жестких предположений и ограничений);

• пренебрежение динамическими свойствами процессов.

4.5.2. Декомпозиция

В общем случае конечной целью декомпозиции является разбиение пространства переменных реального объекта (рис. 4.11) , , , нa подпространств меньших размерностей, в которых учитывается только связь данного выхода с соответствующими переменными.

Рис. 4.11. Декомпозиция

Если любой выход имеет связь с остальными выходами, то декомпозиция практически невозможна. Если общая модель объекта имеет вид неявного выражения, достаточно большой размерности

(4.36)

и выходы y_i с объекта не имеют связи между собой, то сложную модель (4.33.) можно представить в виде совокупности эквивалентных ей n более простых частных моделей для каждого из выходов

, (4.37)

Благодаря проведенной декомпозиции системы значительно облегчается задача ее теоретического исследования.

4.5.3. Макромоделирование и метод адаптивной модели

При использовании метода макромоделирования в исходном пространстве переменных оставляются только те из них, которые влияют на выходные переменные наиболее сильно. Остальные неучтенные воздействия могут быть учтены в параметрической форме путем изменения коэффициентов при учтенных переменных (в случае мультипликативных воздействий) либо путем в ведения свободных членов (для аддитивных воздействий). При построении упрощенных моделей с учетом только существенных факторов широко используется метод адаптивной модели.

Определение 1.39. Адаптивной моделью называется модель коэффициенты которой подстраиваются таким образом, чтобы некоторая мера расхождения (невязка) выходов модели и объекта принимала допустимые (минимальные) значения.

Для этого используют критерии минимизации невязок. Те переменные, которые стабилизируются и не приводят к изменению выходных переменных, в модели не отражаются.

Структура упрощенной модели, называемой макромоделью, может быть трехканальной с каналом управления u и каналами контролируемых x и неконтролируемых z воздействий, двухканальной и одноканальной (рис. 4.12.)

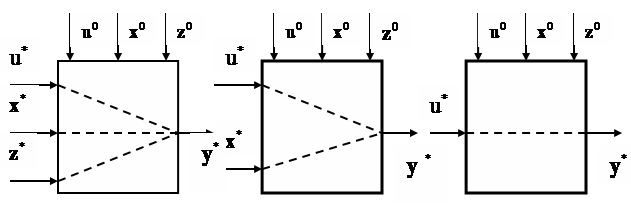
Рис. 4.12. Процесс упрощения модели

Учет возмущений в двухканальных и и в одноканальных моделях производится параметрически за счет подстройки коэффициентов оставшихся каналов.

Полная математическая модель

. (4.38)

Трехканальная макромодель

.  (4.39)

Двухканальная макромодель

.  (4.40)

Одноканальная макромодель

,  (4.41)

, , , − векторы контролируемых переменных, причем выполняются условия , , , свидетельствующие о сокращении числа переменных в макромодели; − вектор настраиваемых коэффициентов; , , − векторы неконтролируемых переменных.

Рассмотрим в качестве примера идею одного из методов адаптации моделей (компенсационный метод) (рис. 4.13).

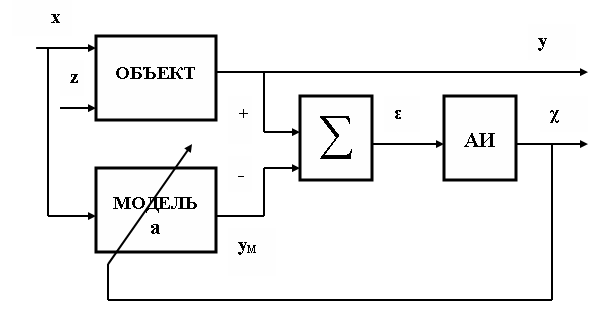
Рис. 4.13. Компенсационный метод адаптации моделей

На рис.4.13:  сигнал рассогласования выходов объекта и модели; АИ — алгоритм идентификации.

Алгоритм идентификации позволяет настраивать модель объекта по критерию минимума ошибки путем изменения параметров a₁ a₂,... модели (a_i* оптимальное значение параметра a_i). Приведенная выше схема работает хорошо, если на ее выход подаётся сигнал без помех. При наличии шума на входе ставится задача подавления помех, которую обычно решают с помощью дифференциальных схем, содержащих полосовые фильтры (дифференциальный метод).