Аналитическое решение:

Гармонические модели применяются в случае доминирующего влияния периодической составляющей на динамику изменений контролируемого параметра процесса. Задача идентификации состоит в построении наилучшего приближения кривой динамики процесса одной или несколькими гармоническими функциями. Периоду изменений контролируемого параметра соответствует частота первой гармоники . В случае отсутствия достоверной информации о начальной фазе следует воспользоваться теоретической моделью следующего вида

.

Модель состоит из трёх базисных функций , , . Коэффициенты модели , , вычисляются по результатам наблюдений за динамикой процесса, представленным выборкой объёмом отсчётов контролируемого параметра процесса , выполненных в дискретные моменты времени . Оптимальные оценки коэффициентов , , минимизируют квадратичный функционал

Из условий минимума функционала , , следует система трёх линейных алгебраических уравнений для вычислений коэффициентов модели

В канонической форме записи система уравнений имеет вид

В системах автоматического регулирования интервал стационарности меньше периода изменений контролируемого параметра процесса и условие ортогональности базисных функций, как правило, не выполняется для полученной выборки результатов наблюдений за динамикой процесса. Матрица системы уравнений не является диагональной и вычисление искомых коэффициентов выполняется методами Крамера, Гаусса или Зейделя.

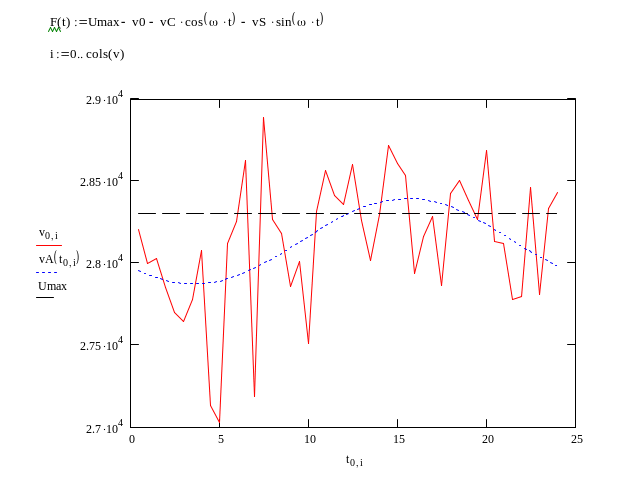
Гармоническая модель позволяет решать задачу цифрового регулирования напряжения контактной сети. Из-за суточных изменений напряжения возникает необходимость коммутации обмоток трансформатора. Она осуществляется в зависимости от соотношения между максимально допустимым значением напряжения и текущим значением тренда. В микропроцессорном блоке регулирования сигнал на переключение обмоток формируется в момент , когда функция меняет знак. Аналогичное соотношение определяет момент переключения при пересечении трендом нижнего значения напряжения .

Решение в системе Math cad: