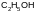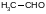Глава I равновесие органических реакций

Равновесные соотношения при химических реакциях имеют важ­ное значение для предсказания возможности их протекания и для выявления условий процесса, термодинамически благопри­ятных для его практической реализации. Они необходимы так­же при кинетическом описании процесса, его моделировании и оптимизации.

Равновесные соотношения определяют двумя путями: термо­динамическим расчетом или экспериментально. В первом слу­чае вначале находят константу равновесия и по ней рассчиты­вают состав равновесных смесей, а во втором, наоборот, по со­ставу равновесных смесей находят константу равновесия. По­следняя часто является действительно постоянной величиной только при выражении ее через равновесные активности

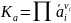(I-1)

где ν_i—стехиометрические коэффициенты участников реакции с соответствующим знаком, 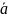и К_а - безразмерные равновес­ная активность и константа равновесия.

Подавляющее число процессов химической технологии про­текает при постоянном или мало меняющемся давлении, когда равновесие характеризуется энергией Гиббса (другие, менее верные ее названия - свободная энергия, изобарно-изотермический потенциал). Изменение энергии Гиббса при химической реакции описывается уравнением:

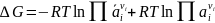(I-2)

Если исходные реагенты находятся в так называемом стандарт­ном состоянии (т. е. при a_i = 1), второй член уравнения превра­щается в нуль и получается известная изотерма Вант-Гоффа

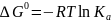(I-3)

где ∆G⁰ - стандартное изменение энергии Гиббса при химиче­ской реакции. В свою очередь, последняя связана со стандарт­ным изменением энтальпии и энтропии реакции соотношением:

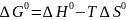(I-4)

Эти уравнения являются основой расчета равновесий и в то же время основой экспериментального определения термодинамиче­ских свойств. Напомним, что при равновесии ∆G (а не ∆G⁰) равна нулю, и знак именно этой величины определяет направ­ление реакции.

Расчет констант равновесия газофазных реакций по термодинамическим данным

Для газов и паров за стандартное принято состояние вещества в виде идеального газа при давлении 1 ат (0,1013 МПа ≈ 0,1 МПа). Именно для такого состояния и температуры 298 К в термодинамических таблицах, имеющихся в моногра­фиях и справочниках, приводятся данные о стандартной энер­гии Гиббса и энтальпии образования соединений из простых веществ, а также об их абсолютной энтропии. Первые две ве­личины обозначают ∆G⁰_f,,298 и ∆H⁰_ƒ,298 (где индекс ƒ происходит от англ. formation), а последнюю S⁰_ƒ,298. Если соединение при указанных условиях (1 ат, или 0,1013 МПа, и 298 К) является жидким или твердым, эти данные соответствуют его фиктивно­му состоянию в виде идеального газа. В свою очередь, ∆G⁰_ƒ,298 и ∆H⁰_ƒ,298 относятся к образованию соединения из простых ве­ществ (0₂, Н₂, С и др.) в их обычном для 0,1 МПа и 298 К га­зообразном, жидком или твердом состоянии в виде наиболее стабильной модификации (значения ∆H⁰_ƒ,298 и S⁰_ƒ,298 для неко­торых органических веществ приведены в качестве примера ни­же, в табл. 3).

Изменение соответствующих характеристик при химической реакции нетрудно вычислить как их сумму для продуктов и ис­ходных реагентов с учетом величины и знака стехиометрических коэффициентов:

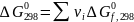
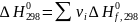
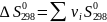(I-5)

Если в реакции участвуют простые вещества, то для них ∆H⁰ и ∆G⁰ при всех температурах приняты равными нулю, но надо учитывать их абсолютную энтропию.

После расчета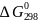 , если необходимо, определяют величи­ну 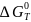при интересующей температуре реакции, для чего су­ществует ряд способов. Перед рассмотрением их отметим, что входящая в уравнение (I-1) активность для идеального газа равна соотношению его парциальных давлений в данном и стан­дартном состояниях P_i/P_i°. В технической системе единиц P_i° равнялось 1 ат, поэтому безразмерная активность идеального газа равнялась его давлению в атмосферах. Этому соответство­вала и величина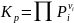 , имеющая размерность 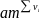и на­ходимая по уравнению 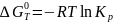. При переходе к СИ это соответствие нарушилось, вследствие чего можно рекомендовать такую процедуру: по последнему уравнению находят вначале 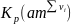, а затем пересчитывают ее в единицы СИ, т.е. .

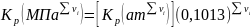Наиболее простой способ расчета констант равновесия для идеальных газов, пригодный для приближенной их оценки или выявления термодинамической возможности данного превра­щения, состоит в использовании уравнения (I-4) в предположе­нии, что энтальпия и энтропия реакции не зависят от температу­ры. Так, для реакции 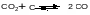находим по таблицам:

для CO₂

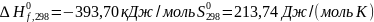
для CO

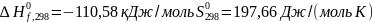
для C

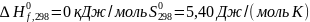
(графит)

Из этих данных вычисляем:

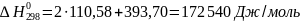
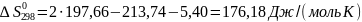
Отсюда при 1000 К энергия Гиббса равна:

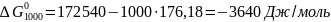
Теперь по уравнению (I-3) рассчитываем:

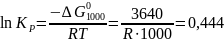
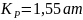
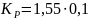
В действительности при точном расчете К_р = 0,190 МПа.

При подобном расчете иногда выражают константу равно­весия как функцию температуры в соответствии с уравнением:

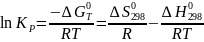(I-6)

По нему легко предсказать область температур, при которой константа равновесия становится достаточно большой.

В действительности термодинамические функции определен­ным образом зависят от температуры, что нужно учитывать при точном расчете равновесий. Для энергии Гиббса эта зависи­мость такова:

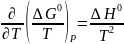(I-7)

Практическое применение этого уравнения осложняется тем, что стандартное изменение энтальпии реакции также зависит от температуры в соответствии с законом Кирхгоффа:

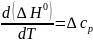(I-8)

В уравнении (I-8) ∆c_p представляет собой разность изобарных теплоемкостей продуктов и исходных веществ, которую рассчи­тывают с учетом стехиометрии процесса:

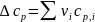(I-9)

В соответствии с уравнением (I-8) и дифференциальным выра­жением TdS = c_pdT получаем такие интегральные зависимости стандартной энтальпии и энтропии реакции:

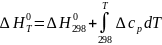
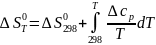
Таким образом, точное уравнение для энергии Гиббса таково:

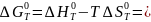
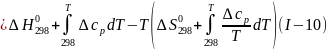
Одно из приближенных его решений, предложенное Темкиным и Шварцманом, основано на применении регрессионного урав­нения зависимости теплоемкости веществ от температуры:

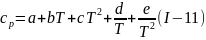
Коэффициенты уравнения определяют экспериментально, причем обычно бывает достаточно трех первых членов уравне­ния (I-11). Значения коэффициентов для разных веществ име­ются в термодинамических таблицах (для примера см. табл. 3).

Используя уравнения (I-9), (I-10) и (I-l1),получаем

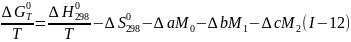
Где

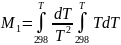
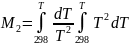
а ∆a, ∆b, ∆c - суммы коэффициентов уравнений теплоемкости для реагентов и продуктов, полученные в соответствии с урав­нениями (I-11) и (I-9). Интегралы Темкина - Шварцмана М₀, М₁, М₂, М_-1 и М_-2,

включающие под знаком второго интеграла температуру в соответствующей степени, зависят только от тем­пературы. Они заранее рассчитаны с интервалом в 50 и 100 градусов, а внутри расчетных интервалов значения каждого инте­грала следует находить интерполяцией (табл. 1).

Таблица 1. М-интегралы Темкина — Шварцмана

М-интеграл	М-интегралы при разной температуре
	300К	400К	500К	600К	700 К	800 К	900 К
М0	0,000	0,0392	0,1133	0,1962	0,2794	0,3597	0,4361
М1∙10-3	0,000	0,0130	0,0407	0,0759	0,1153	0,1574	0,2012
М2∙10-3	0,000	0,0043	0,0149	0,0303	0,0498	0,0733	0,1004
М-2∙105	0,000	0,0364	0,0916	0,1423	0,1853	0,2213	0,2521

Пример. Дегидрирование этанола в ацетальдегид

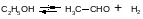
проводят в газовой фазе. Требуется рассчитать константу равновесия этой реакции при 473 К. Из табличных данных имеем:

Вещество	∆H0ƒ,298, кДж/моль	S0ƒ,298, Дж/моль	a	b∙103	c∙106
	-235466	282,2	14,98	208,7	71,14
	166467	265,9	31,07	121,5	-3,60
	0	130,7	29,09	-0,837	2,013

Отсюда имеем:

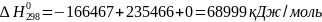
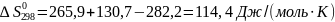
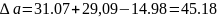
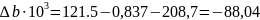
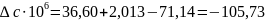
Из табл. 1 интегралы Темкина-Шварцмана при 473 К равны:

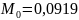
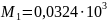
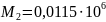
Тогда энергия Гиббса получится такой:

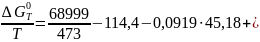
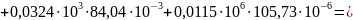
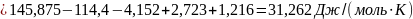
Поскольку 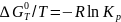, то

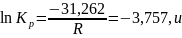
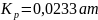или 0,00236МПа (по экспериментальным данным 0,0121 ат, или 0,00122 МПа).

При отсутствии полных термодинамических данных оказы­вается полезным расчет, использующий прямое интегрирование температурной зависимости ∆G⁰ - уравнение (I-7). В этом ва­рианте приходится учитывать влияние температуры на стан­дартный тепловой эффект реакции, которое дается интеграль­ной формой закона Кирхгоффа

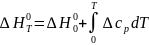
с подстановкой 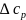в виде зависимости (I-11)

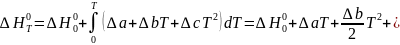
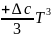
причем через 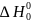обозначена постоянная интегрирования. Это выражение можно использовать для интегрирования уравнения (I-7):

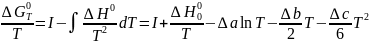
Или

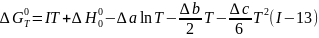
В уравнении (I-13) I , как и ∆Н₀⁰, является константой интегри-рования, следовательно, расчетная форма уравнения должна включать две численные величины I и ∆H°₀, которые могут быть, найдены из соответствующих экспериментов. Так, если известны ∆G⁰ или константы равновесия реакции при двух разных темпера­турах, то их подстановка в левую часть уравнения (I-I3) позво­ляет найти I и ∆H°₀. Если имеются данные о тепловом эффекте, то можно найти ∆Н°₀, и тогда достаточно знать ∆G⁰ при той же или при иной температуре, чтобы, зная H°₀, вычислить I. Возможны и некоторые другие варианты, но очевидно, что для расчета двух постоянных интегрирования всегда требуется не менее двух экспериментально найденных величин ∆G⁰ или их сочетания с ∆H°, ∆S° и т. д.

По своей точности такой расчет ∆G°_T не может превосходить метод Темкина — Шварцмана.

Пример. Для рассмотренной выще реакции дегидрирования этанола в ацетальдегид известны экспериментальные значения lgK_p для 150 и 250 ^оС соответственно равные -2,796 и -0,635 (давление в атмосферах). С помощью их, а также известных коэффициентов уравнения теплоемкости, определяем постоянные интегрирования:

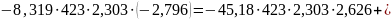
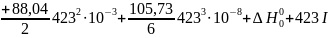
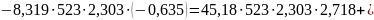
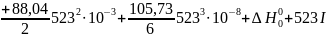
Вычитанием уравнений находим I≈106,82 и после подстановки ∆H°₀=83842,14. Таким образом, уравнение для расчета lgК_р приобретает вид:

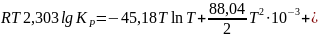
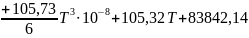
Для 200 °С оно дает lgК_р = 1,596, К_р=0,02536 ат (0,002569 МПа), что близ­ко к результату предыдущего расчета.

Равновесие для реальных газов. При повышенном давлении или в состоянии, близком к насыщенному пару, газы перестают быть идеальными, и для них используют выражения констант

Таблица 2. Коэффициенты летучести реальных газов γ при различных приведенных температурах ϴ и давлениях π

π	γ при разной приведенной температуре ϴ
	0,7	0,85	1,0	1,2	1,5	2,0	5,0	10	15
0,1	0,870	0,914	0,964	̶	̶	̶	̶	̶	̶
0,3	̶	0,806	0,888	0,960	̶	̶	̶	̶	̶
0,6	̶	̶	0,774	0,880	0,970	̶	̶	̶	̶
1,0	̶	̶	0,611	0,814	0,926	0,976			̶
2	̶	̶	0,385	0,668	0,822	0,956	1,040	1,025
5	̶	̶	0,226	0,464	0,736	0,922	1,076	1,048	1,038
10	̶	̶	0,202	0,434	0,730	0,964	1,167	1,102	1,072
15	̶	̶	̶	0,532	0,826	1,100	1,274	1,160	1,110

равновесия и изотермы Вант-Гоффа через активности [(I-1) и (I-3)]. Чтобы сохранить общий вид термодинамических зависи­мостей для реальных газов, введено понятие летучести, или фугитивности ƒ, удовлетворяющее условию 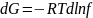. При этом стандартная летучесть f⁰ принята равной летучести газа в идеальном состоянии при давлении 0,1013 МПа. Активностью называют соотношение летучестей реального газа в данном и стандартном состояниях (a_i = f_i/f_i⁰), а коэффициентом летуче­сти - соотношение его летучести и парциального давления (γ_i = f_i/P_i). При давлении 1 ат реальный газ можно принять за идеальный, и поэтому ƒ⁰= 1 ат. Тогда

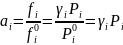(I-14)

где Р_i выражено в ат. Для идеального газа γ_i =1, a_i =P_i ат и

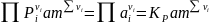. В случае реального газа коэффи­циент летучести находят по принципу соответственных состоя­ний, согласно которому значения γ для реальных газов являют­ся одинаковыми, если газы находятся при тех же приведенных температурах ϴ = Т/Т_кр и давлениях π = Р_общ/Р_кр (при определе­нии π берут не парциальное давление, а общее, так как газ ис­пытывает влияние всех компонентов смеси, а для водорода вме­сто критических параметров используют Р_кр+8 ат и T_кр+8 К). Все это позволяет использовать для нахождения γ любых ре­альных газов одни и те же графики или таблицы (табл. 2). Изотерму Вант-Гоффа для реальных газов можно преобразо­вать в следующую форму:

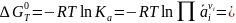
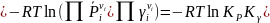(I-15)

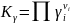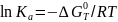Здесь К_р выражено в ат, а является произведением коэффициентов летучести участников реакции в степени, равной их стехиометрическим коэффициентам с соответствующим зна­ком. Следовательно, для расчета искомой величины К_р для реальных газовых смесей необходимо: 1) найти, как для идеаль­ных газов, ∆G_Т⁰ и по ней величину ; 2) по приведенным параметрам определить γ_i и К_i после чего вы­числить .

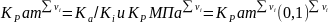Пример. Найти К_Р реакции синтеза метанола в газовой фазе при 300^oС и 30 МПа

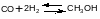
если известно, что ∆G⁰₅₇₃= 39769 Дж/моль, а критические параметры таковы:

Вещество	Tкр , К	Ркр , МПа
СО	134,1	3,50
Н2	32,0	1,28
СН3ОН	513,0	7,87

Рассчитываем приведенные параметры и находим:

Вещество	ϴ	π	γ
СО	4,27	8,57	2,14
Н2	14,25	14,40	1,11
СН3ОН	1,12	3,81	0,38

Отсюда

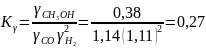
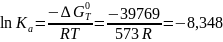
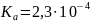
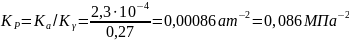
Очевидно, что по сравнению с идеальным состоянием смеси К_р увеличивается в 1 : 0,27 = 3,7 раза.