
- •Теория химических процессов основного органического и нефтехимическогосинтеза
- •Глава I 28
- •Глава II 64
- •Предисловие
- •Безразмерные характеристики материального баланса реакции. Парциальные молярные балансы
- •Глава I равновесие органических реакций
- •Расчет констант равновесия газофазных реакций по термодинамическим данным
- •Приближенные методы расчета констант равновесия
- •Константы равновесия жидкофазных реакций
Безразмерные характеристики материального баланса реакции. Парциальные молярные балансы
Кроме мольных количеств и потоков в химии и технологии большое значение имеют безразмерные характеристики материального баланса — степень конверсии, селективность и выход.
Степень конверсии — доля прореагировавшего исходного реагента относительно его начального количества:
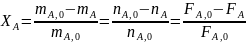 (0-6)
(0-6)
В
таком написании степень конверсии может
меняться от 0 до 1, но ее нередко выражают
в процентах, умножая правые части,
предыдущих выражений на 100. При этом
обычно степень конверсии определяют
по основному исходному реагенту А , но
ее можно аналогично записать и для
других реагентов [например,
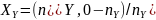 ].
].
В предыдущем примере дегидратации этанола степень его конверсии составляет:
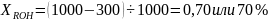
В разных процессах химической технологии степень конверсии изменяется от 4—5 до почти 100%. Из уравнения (0-6) следует:
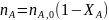
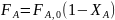 (0-7)
(0-7)
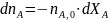
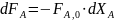 (0-8)
(0-8)
Для
простых и обратимых реакций, когда
имеются единственное независимое
превращение и одно ключевое вещество,
степень конверсии — вполне достаточная
характеристика материального
баланса. Действительно, зная
 ,
легко рассчитать
FA
по
уравнению (0-7), n
(F)
по формуле (0-3) и затем все ni
(Fi)
по уравнению (0-4). Кроме того, для любой
простой или обратимой реакции
,
легко рассчитать
FA
по
уравнению (0-7), n
(F)
по формуле (0-3) и затем все ni
(Fi)
по уравнению (0-4). Кроме того, для любой
простой или обратимой реакции
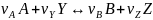
в дополнение к соотношению (0-7) легко вывести зависимость ni(Fi)от nА,0 (FА,0) и степени конверсии основного реагента ХA:
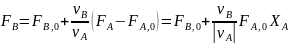
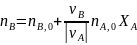
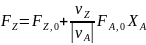
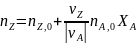
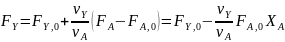
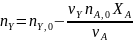
где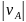 -
абсолютное значение стехиометрического
коэффициента при А.
-
абсолютное значение стехиометрического
коэффициента при А.
Для сложных реакций, имеющих более одного ключевого вещества, степень конверсии показывает лишь долю превращенного реагента, но не дает представления о направлениях его превращения, которое определяется селективностью и выходом.
Селективность — доля (или процент) превращенного исходного реагента, израсходованная на образование данного продукта. При этом всегда учитывают только химические превращения в реакторе, исключая какие-либо иные потери веществ (кроме их расходования на образование побочных продуктов). Другими словами, селективность можно определить как отношение количества полученного продукта к его теоретическому количеству, которое могло бы образоваться из превращенного реагента при отсутствии побочных реакций и потерь. Теоретическое количество легко рассчитать по суммарной реакции образования данного продукта из исходных реагентов, применяя к ней уравнения (0-3):

Тогда получим выражение для селективности Ф
ФiA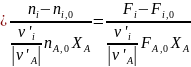 (0-9)
(0-9)
в котором двойной индекс при Ф означает, что селективность определена для продукта i по основному реагенту А. Ее можно аналогичным образом выразить и по другому реагенту. Когда исходное вещество является единственным или известно, по какому из реагентов определяется селективность, индекс А (или Y) может быть опущен.
В уравнении (0-9) член
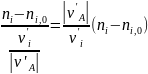
соответствует количеству исходного реагента, израсходованному на образование данного ключевого вещества. Очевидно, что сумма их для всех ключевых веществ будет равна FA,0 XA, откуда вытекает соотношение:
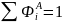 (0-10)
(0-10)
Так, для ранее рассмотренного примера дегидратации этанола получим:
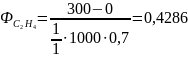
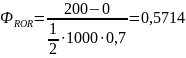
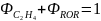
Селективность по целевому продукту показывает долю полезно использованного сырья; она является важной характеристикой катализаторов, условий проведения процесса и типа реакторов. На практике селективность по целевому продукту изменяется от 50-60 до 100%, причем повышение селективности - одна из важнейших задач химической технологии.
Выход — это далеко не однозначное понятие. Иногда под ним понимают абсолютное количество полученного продукта (в г, кг, моль и кмоль), но чаще выход выражают в долях единицы или в процентах на взятое сырье. Кроме того, выход применяют для характеристики систем разного масштаба - только реакционного аппарата (химический выход), какого-либо узла производства или технологической схемы в целом, когда учитывают не только расход сырья на химические реакции, но и различные потери (технологический выход). Далее мы будем применять понятие только химического выхода.
Химический выход равен мольному количеству полученного продукта i,отнесенному к его теоретическому количеству. Следовательно, выражение для выхода легко получить из формулы (0-9) при ХA=1:
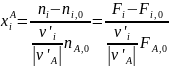 (0-11)
(0-11)
Выход можно рассчитывать и по второму реагенту (xiY), причем в литературе встречаются и другие обозначения выхода (Xi, если реагент является единственным или определенно известно, по какому реагенту рассчитывается выход, а также х, у, z ит.д).
Из формул (0-9) и (0-11) вытекает, что выход равен произведению селективности на степень конверсии:

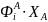 (0-12)
(0-12)
При этом сумма выходов ключевых веществ по основному реагенту А с учетом уравнения (0-10) равна степени конверсии этого реагента:
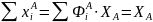 (0-13)
(0-13)
Рассчитаем выходы и проверим полученные соотношения для примера дегидратации этанола:
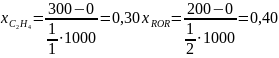
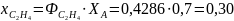
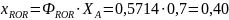
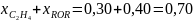
Из уравнения (0-11) мольные количества или потоки продуктов можно выразить через их выходы:
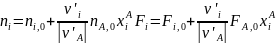 (0-14)
(0-14)
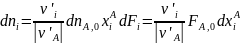 (0-15)
(0-15)
Последние уравнения широко используют в химической кинетике и при расчете реакторов. Очевидно, что при расчете материальных балансов процесса все или часть исходных данных (за исключением ni,0 или Fi,0) может быть задана безразмерными характеристиками — степенью конверсии, селективностью или выходом. Тогда, используя выведенные уравнения, легко рассчитывают мольные количества или потоки всех веществ и составляют таблицу материального баланса.
Парциальные молярные балансы. На безразмерных характеристиках реакций основаны расчеты так называемых парциальных молярных балансов, составляемых на 1 моль основного исходного реагента А. При этом начальный состав смеси также выражают через безразмерные величины, а именно мольные соотношения других веществ, в том числе инертных, к основному реагенту А:
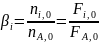 (0-16)
(0-16)
Безразмерные формы уравнений баланса составляют по независимым суммарным реакциям, деля выражения (0-5) на nA (FA,0):
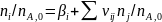
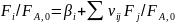

Здесь
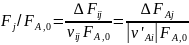 .
Величина
.
Величина
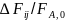 есть степень полноты или частная
степень конверсии основного реагента
по данной суммарной реакции и обозначается
как Xj,изменяющаяся
от 0 до 1. Если какое-либо ключевое вещество
образуется только по этой
реакции, то имеем
есть степень полноты или частная
степень конверсии основного реагента
по данной суммарной реакции и обозначается
как Xj,изменяющаяся
от 0 до 1. Если какое-либо ключевое вещество
образуется только по этой
реакции, то имеем
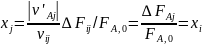
т. е. его выход равен степени полноты реакции. Следовательно, получаем уравнение парциального молярного баланса:
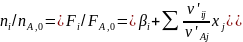 (0-17)
(0-17)
Рассчитаем парциальный молярный баланс реакции дегидратации этанола:
C2H5OH C2H4 + H2O 2 C2H5OH (C2H5)2O + H2O
Согласно предыдущему, имеем:
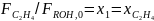
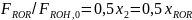
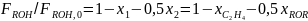
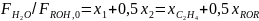
КОНЦЕНТРАЦИИ, ПАРЦИАЛЬНЫЕ ДАВЛЕНИЯ И МОЛЬНЫЕ ДОЛИ.
Кроме мольных количеств или потоков веществ и безразмерных характеристик баланса важное значение имеют концентрации, парциальные давления и мольные доли, на которых основаны расчеты термодинамики и кинетики реакций, а также химических реакторов.
Концентрация соответственно для периодических и непрерывных процессов определяется как отношение мольного количества (мольного потока) вещества к объему V (к объемному потоку W), в котором равномерно распределено данное вещество:
 (0-18)
(0-18)
При этом объем (в л или м3) и объемный поток (в л или м3 в секунду, минуту или час) особенно для газофазных реакций необходимо привести к давлению и температуре в реакторе, учитывая объем всех компонентов системы, в том числе разбавителей.
Нередко объем или объемный поток остаются постоянными во время реакции. Это типично для жидкофазных процессов, а для газофазных встречается в тех случаях, когда реакция протекает при постоянных общем давлении и температуре без изменения числа молей веществ или без промежуточного разбавления смеси. Для таких процессов справедливы концентрационные формы всех выведенных ранее уравнений баланса и формул для расчета безразмерных характеристик реакций, т. е. в эти уравнения можно вместо ni (Fi) подставлять Сi.
Для
идеальных газов их концентрации
пропорциональны. парциальным
давлениям
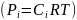 ,
и, следовательно, те же уравнения подходят
и для парциальных давлений веществ. При
этом последние являются более удобной
характеристикой состояния газа, так
как при постоянном общем давлении они,
в
отличие
от концентраций, не зависят от температуры.
,
и, следовательно, те же уравнения подходят
и для парциальных давлений веществ. При
этом последние являются более удобной
характеристикой состояния газа, так
как при постоянном общем давлении они,
в
отличие
от концентраций, не зависят от температуры.
Более сложные соотношения существуют для реакций, протекающих с изменением объема. При жидкофазных процессах это бывает при поглощении какого-либо газа жидкостью или при разложении жидкого вещества с образованием летучих продуктов. Тогда объем жидкой фазы в любой момент реакции находят с помощью коэффициента изменения объема ε по уравнению
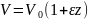 (0-19)
(0-19)
где V0 и V — начальный и текущий объемы, a z — некоторая функция, от которой зависит изменение объема (например, степень конверсии или число присоединившихся молей газа). При этом коэффициент изменения объема определяется выражением
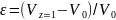 (0-20)
(0-20)
и является положительным при увеличении объема смеси во время реакции и отрицательным при его уменьшении. Тогда текущая концентрация вещества равна:
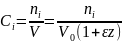 (0-21)
(0-21)
Пример. При оксиэтилировании спиртов для получения неионогенных ПАВ барботируют газообразный этиленоксид через жидкую реакционную массу при катализе гидроксидом натрия:
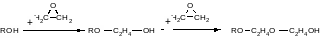
Найти концентрацию NaOH, когда к 1 моль спирта присоединилось 10 моль этиленоксида, если начальная концентрация NaOH равна Со=0,022 моль/л, а коэффициент изменения объема при поглощении одной оксиэтильной группы равен ε = 0,12. Находим:
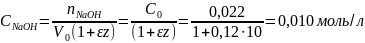
Для газофазных процессов изменение объема обычно происходит из-за неравенства числа молей веществ во время реакции (разложение, присоединение и др.). Его можно учитывать с помощью введенных выше коэффициентов изменения объема, которые для газообразного состояния веществ зависят отначального и конечного числа молей смеси:
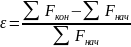 (0-23)
(0-23)
Например,
для реакции
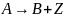 в отсутствие разбавителей имеем
в отсутствие разбавителей имеем
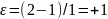 ,
а для превращения
,
а для превращения
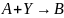 при эквимольном соотношении реагентов
и в отсутствие разбавителей
при эквимольном соотношении реагентов
и в отсутствие разбавителей
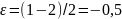 . Для первой реакции при мольном
соотношении инертного разбавителя β0
получим:
. Для первой реакции при мольном
соотношении инертного разбавителя β0
получим:
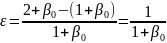
Для второй реакции при мольном избытке второго реагента βY имеем:
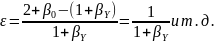
Особенно удобно использовать коэффициенты изменения объема для простых и обратимых реакций, когда имеем:
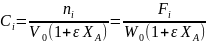 (0-23)
(0-23)
При подстановке Fi как функции Fa,0 и ХА оказывается, что Ci выражается через начальную концентрацию (CA,0 = Fa,0/W0). Например, для реакции имеем:
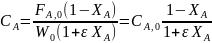
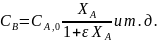
Последние уравнения справедливы при Т=const. Из-за пропорциональности концентраций парциальным давлениям можно записать соотношения, не зависящие от температуры:
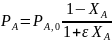
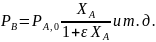
Более общий способ расчета парциальных давлений состоит в использовании мольных долей веществ, которые находят из парциальных молярных балансов
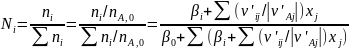 (0-24)
(0-24)
где β0 - мольное соотношение инертных разбавителей и основного реагента А в исходной смеси. После этого парциальные давления вычисляют по формуле
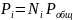 (0-25)
(0-25)
где Pобщ - общее давление смеси, которое для большинства процессов можно считать постоянным.
Пример. При совмещенном дегидрохлорировании и хлорировании 1,1,2,2-тетрахлорэтана протекают такие суммарные реакции:
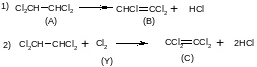
Вывести уравнения для парциальных давлений веществ с учетом содержания инертных примесей и мольного соотношения реагентов βY. Рассчитать эти давления при βY=0,55, xв=0,45, хс =0,54, содержании в хлор-газе 7% инертных примесей и общем давлении 0,12МПа.
Имеем уравнения парциального молярного баланса:
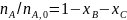
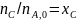
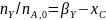
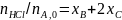
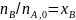

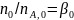
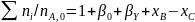
При содержании в хлор-газе 7% инертных примесей имеем:
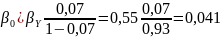
Отсюда получаем:
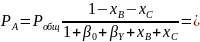
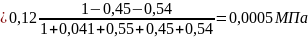
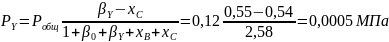
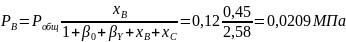
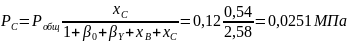
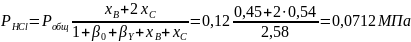
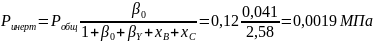
Проводим проверку:
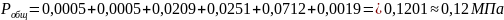
Вопросы и упражнения
1 .
Простая реакция C6H6+3H2
C6H12
проводится
при мольном соотношении
H2
:
C6H6
=
10:1. Рассчитайте баланс реакции, если
начальный поток бензола составляет 100
кмоль/ч, а степень его конверсии равна
0,95. Составить таблицу материального
баланса.
.
Простая реакция C6H6+3H2
C6H12
проводится
при мольном соотношении
H2
:
C6H6
=
10:1. Рассчитайте баланс реакции, если
начальный поток бензола составляет 100
кмоль/ч, а степень его конверсии равна
0,95. Составить таблицу материального
баланса.
2.Для предыдущей реакции выразите мольные потоки компонентов смеси через начальный мольный поток бензола, степень его конверсии и соотношение реагентов βY.
3. При окислении этилена протекают реакции
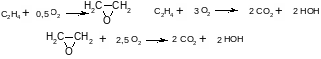
Составьте стехиометрическую матрицу, найти число независимых реакций, выберите независимые реакции и ключевые вещества.
4. Для предыдущей реакции провести материальный расчет для условий: начальный мольный поток этилена равен 150 кмоль/ч, степень его конверсии 0,40, селективность образования этиленоксида 0,70, мольное соотношение кислорода и этилена βY=0,60. Составьте таблицу материального баланса.
5. Для реакции из примера 3 составьте общие уравнения зависимости мольных потоков веществ от начального мольного потока этилена, βY, выходов этbленоксида и диоксида углерода.
6. Какое уравнение связывает между собой степень конверсии, селективность и выход продукта?
7. Составьте парциальный молярный баланс для простой реакции из примера 1. Выведите уравнения парциальных давлений компонентов смеси в зависимости от начального давления бензола и общего давления, если известно, что реакция проводится в газовой фазе без посторонних разбавителей и при начальном мольном отношении Н2: C6H5 = βY.
8. При дегидрировании н-бутана протекают следующие суммарные реакции
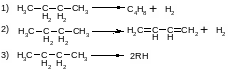
где
RH—
молекулы СН4
и С3Н6
или С2Н6
н С2Н4.
Составьте парциальный молярный баланс
процесса и выразите парциальные давления
всех веществ через выходы бутена,
бутадиена и низших углеводородов, если
реакция протекает без посторонних
разбавителей. Рассчитайте парциальные
давления, если
Р
общ
=
0,02 МПа,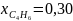 ;
;
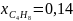 ,
а
селективность процесса по смеси-С4Н8
и С4Н6
составляет 0,90.
,
а
селективность процесса по смеси-С4Н8
и С4Н6
составляет 0,90.
