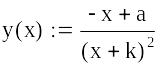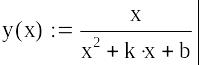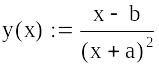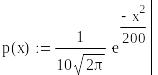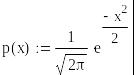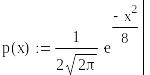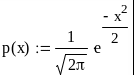14. Complete and solve differential equation for the next problem.
There is a lake with volume V. The damaging waste flows into the lake with constant speed g (gramme per hour). The clear water flows in lake by stream with speed w (m3 per hour). Another stream flows out from the lake with the same speed (thus the volume of the lake remains constant).
Find dynamics of the pollution as a waste concentration (in g/m3) vs time
Find the time that is required to make lake clear from the waste concentration 1g/m3 if pollution stops.
Variant N |
g |
w |
V |
Variant N |
g |
w |
V |
1 |
10 |
7 |
2·106 |
11 |
12 |
9 |
8·106 |
2 |
12 |
6 |
3·106 |
12 |
13 |
8 |
2·106 |
3 |
14 |
5 |
4·106 |
13 |
14 |
7 |
3·106 |
4 |
16 |
4 |
5·106 |
14 |
14 |
6 |
4·106 |
5 |
19 |
5 |
6·106 |
15 |
15 |
5 |
2·106 |
6 |
15 |
6 |
7·106 |
16 |
16 |
4 |
5·106 |
7 |
11 |
7 |
8·106 |
17 |
17 |
5 |
6·106 |
8 |
9 |
5 |
9·106 |
18 |
18 |
4 |
7·106 |
9 |
7 |
4 |
8·106 |
19 |
19 |
6 |
106 |
10 |
10 |
6 |
7·106 |
20 |
20 |
7 |
9·106 |
15.The dependence between y (Electric current) and X (Voltage) is given as a table.
x |
0
|
5 |
10 |
15 |
20 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
y |
0 |
2 |
8 |
50 |
145 |
160 |
190 |
220 |
222 |
279 |
270 |
276 |
270 |
279 |
Build the mathematical model as function according to variant number. Unknown coefficients find using least squares method. Obtain the predicting value of current for the voltage 25 using built model. Plot the graph with given points (boxes) and built function (line).
1. |
|
11 |
|
2. |
y(x)=a·x2+b·x+c |
12 |
|
3. |
y(x)=k·x3+a·x2+b·x+c |
13 |
y(x)=a·x3+b·x2+c·x |
4. |
|
14 |
|
5. |
|
15 |
|
6. |
y(x)=a·x2+b·x |
16 |
y(x)=a·x4+b·x+c |
7. |
|
17 |
|
8. |
|
18 |
|
9. |
|
19 |
y(x)=a·x4+b·x3+c |
10. |
y(x)=a·x2+b·x |
20 |
y(x)=a·x·exp(–(x–b)2) |
16. Build the graph according the table of values using cubic spline (task for all variants is the same; N is number of variant).
ei
ti
Example: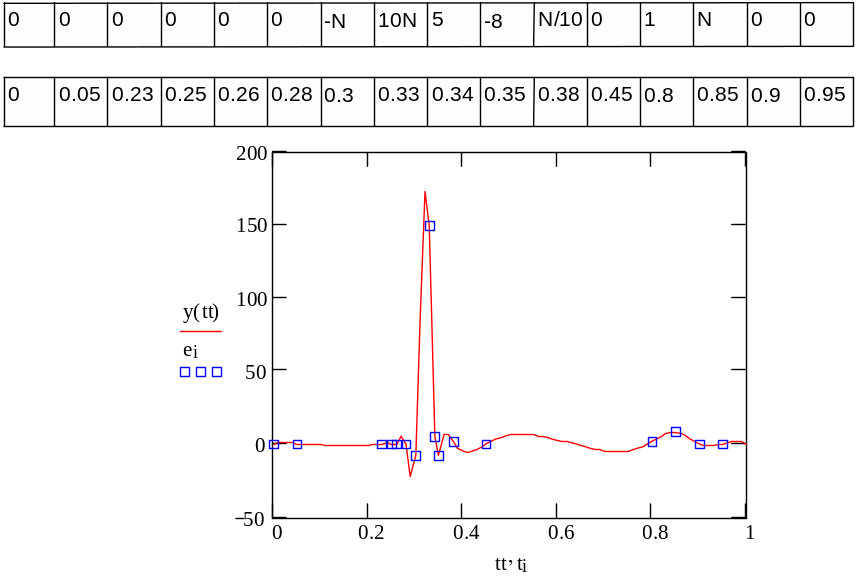
17. Find the maximum or minimum value of the function in consideration of conditions.
N |
Function |
conditions |
find |
N |
Function |
conditions |
find |
1 |
Z(x,y)=x2+y2 |
Z=2x–3y+10 |
max |
11 |
Z(x,y)=x3+5y2 |
Z=x–5y+1 |
max |
2 |
Z(x,y)=x2+2y2 |
Z=4x–3y+8 |
min |
12 |
Z(x,y)=x3–y3 |
Z=4x–5y+2 |
min |
3 |
Z(x,y)=x2–y2 |
Z=x–7y+10 |
min |
13 |
|
|
|
4 |
Z(x,y)=x3+y2 |
Z=x–5y+1 |
max |
14 |
Z(x,y)=x2+y2 |
Z=2x–3y+10 |
min |
5 |
Z(x,y)=x3–y3 |
Z=9x–5y+1 |
max |
15 |
Z(x,y)=x2+2y2 |
Z=4x–3y+8 |
max |
6 |
|
Z=x–y+2 |
max |
16 |
|
Z=0.2x+0.3y+5 |
max |
7 |
|
Z=x+0.1y+2 |
min |
17 |
|
Z=x–2y+1 |
max |
8 |
Z(x,y)=x2–y2 |
Z=2x–3y+4 |
min |
18 |
Z(x,y)=x2–2y2 |
Z=x–6y+11 |
min |
9 |
|
Z=0.1x+y+5 |
min |
19 |
Z(x,y)=x2+y2 |
Z=2x+3y+4 |
max |
10 |
Z(x,y)=x·y |
Z=5 |
min |
20 |
Z(x,y)=x·y |
Z=5–x2 –y2 |
min |
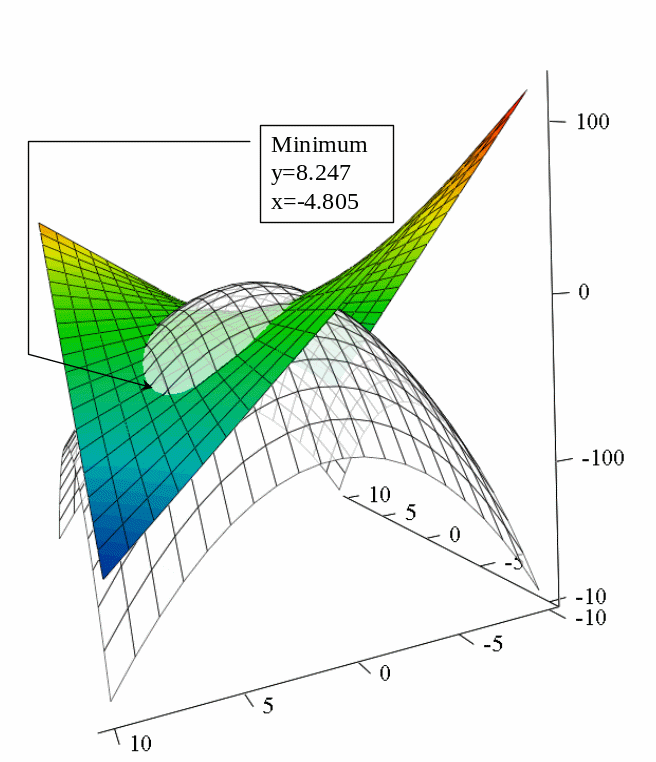
Plot 3D graph of the function and surface of conditions. Save the picture in bit-map and show the point of minimum (maximum).
Example:
The probability distribution of casual value x is given in the table. Calculate the probability of existing x within interval [a, b]. Draw the graph, copy it in the report as a vector graphics and fill by red color the square corresponding probability that has been found.
N |
P(x) |
a |
b |
N |
P(x) |
a |
b |
1 |
|
-1 |
-0.5 |
11 |
|
20 |
600 |
2 |
P(x)=e–x |
1 |
2 |
12 |
P(x)=1 |
0 |
0.1 |
3 |
|
0 |
4 |
13 |
|
2 |
25 |
4 |
|
-1 |
1 |
14 |
|
0 |
1 |
5 |
|
5 |
10 |
15 |
|
-1 |
1 |
6 |
P(x)=0.2e–x/5 |
0 |
0.2 |
16 |
P(x)=1–0.5x |
1 |
1.1 |
7 |
P(x)=2–2x |
0 |
0.3 |
17 |
P(x)=3e–3x |
0 |
1 |
8 |
|
0.5 |
2.2 |
18 |
|
-3 |
|
9 |
|
1 |
1.1 |
19 |
|
0 |
25 |
10 |
|
-3 |
3 |
20 |
|
-2 |
2 |
Example:
