Лабораторна робота №2.4 визначення прискорення вільного падіння за допомогою фізичного маятника

Мета роботи: вивчити вільні коливання фізичного маятника, визначити прискорення вільного падіння за допомогою однорідного стрижня.

Теоретичні відомості

Фізичним маятником називається будь-яке тверде тіло, здатне під дією сили тяжіння коливатися відносно нерухомої горизонтальної осі, яка не проходить через центр мас.

Маятник здійснює гармонічні коливання, відхиляючись на малі кути від положення рівноваги .

Період гармонічних коливань фізичного маятника визначається співвідношенням



(2.4.1)

де – момент інерції маятника відносно осі обертання; – маса маятника; – найкоротша відстань від точки підвішування до центра мас; – прискорення сили тяжіння.

Вісь обертання маятника не проходить через його центр тяжіння, тому момент інерції визначається за теоремою Штейнера:



(2.4.2)

де – момент інерції тіла відносно осі, яка проходить через центр мас і паралельна до осі обертання.

З урахуванням (2.4.2) перепишемо (2.4.1):

 (2.4.3)

Математичний маятник – це матеріальна точка, що підвішена на невагомій нерозтяжній нитці.

Період гармонічних коливань математичного маятника визначається за формулою

 (2.4.4)

де – довжина нитки.

Період малих коливань фізичного маятника іноді записують у вигляді

, де 

(2.4.5)

– зведена довжина фізичного маятника – величина, що чисельно дорівнює довжині такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника.

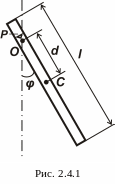
Застосований в цій роботі фізичний маятник має форму тонкого стрижня довжиною l (рис. 2.4.1).

– центр тяжіння,

– точка підвішування, через яку проходить вісь обертання, перпендикулярна до рисунка.

По стрижню може переміщуватися легка трикутна опорна призма Р.

Якщо призма закріплена, стрижень коливається відносно горизонтальної осі О, опираючись нижнім ребром призми на нерухому тверду підставку, що утримується штативом.

Фіксуючи призму в різних точках стрижня, можна змінювати відстань .

Момент інерції однорідного тонкого стрижня відносно осі, що проходить через центр мас,



(2.4.6)

де – маса стрижня; – довжина.

Підставивши (2.4.6) у (2.4.3), одержимо



(2.4.7)

Позначимо , тоді



(2.4.8)

Період коливань можна знайти експериментально, вимірюючи секундоміром час , за який стрижень здійснює повних коливань.



(2.4.9)

Піднесемо до квадрату (2.4.8) і одержимо робочу формулу для обчислення прискорення вільного падіння:



(2.4.10)

Порядок виконання роботи

Таблиця 2.4.1

№ п/п	, м	, м		, с		, с	,
;

Таблиця 2.4.2

,	,	, %