Комплексные числа и действия над ними
1.1. Определение комплексного числа
Пусть существует такое число, квадрат которого равен минус единице. Будем называть это число мнимой единицей и обозначать буквой i (от слова image):
i 2 = 1.
Выражение
z = x + iy,
где x, y — вещественные числа, а i — мнимая единица, называется комплексным числом. Числа x и y в этом равенстве называются вещественной и мнимой частями комплексного числа и обозначаются соответственно
x = Re z, y = Im z.
Числа, у которых
мнимая часть равна нулю:
,
являются чисто вещественными. Таким
образом, множество R
всех вещественных чисел является
подмножеством множества всех комплексных
чисел C.
Числа, у которых
равна пулю вещественная часть:
,
называются чисто мнимыми.
Число
вида
называется комплексно-сопряженным
к числу
.
Очевидно:
,
.
Два комплексных числа равны тогда и только тогда, когда одновременно равны их вещественные и мнимые части:
;
;
В
частности,
и
.
1.2. Действия над комплексными числами
Введем операции над комплексными числами, рассматривая их как многочлены первого порядка относительно мнимой единицы i.
1. Сложение и вычитание.
.
Таким образом, имеем
,
.
Для комплексно-сопряженных чисел получим
,
.
2. Умножение.
При
умножении будем учитывать, что под
мнимой единицей понимается такое число,
квадрат которого равен минус единица,
то есть
.
Тогда получим
.
Таким образом,
,
.
Перемножим два комплексно-сопряженных числа:
.
Следовательно, произведение двух комплексно-сопряженных чисел есть чисто вещественное число.
3. Деление.
Для получения
формулы деления одного комплексного
числа
на другое
воспользуемся тем, что произведение
комплексно-сопряженных чисел есть число
чисто вещественное: чтобы знаменатель
стал вещественным числом, умножим
числитель и знаменатель дроби на число,
сопряженное знаменателю:
.
Таким образом,
;
.
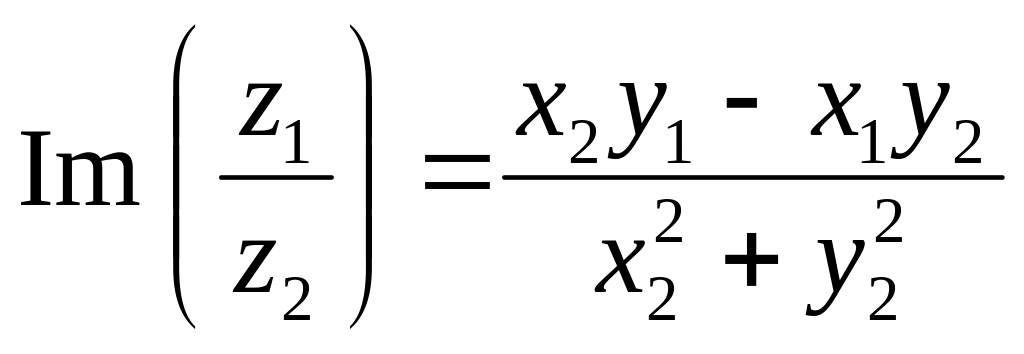Замечание. Вычитание и деление комплексных чисел можно определить, как действия, обратные определениям сложения и умножение, а именно:
1) 
.
2)
,
.
Пример 1.
Пусть
;
.
Тогда:
1) 
;
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
.
Убедимся, что числа, найденные в примерах 5 и 6, взаимно-обратные, т.е. их произведение равно единице:
.
Свойства сложения и умножения комплексных чисел (без доказательств):
1. 
— коммутативность
сложения или перестановочный закон.
2. 
— ассоциативность
сложения или сочетательный закон.
3. 
— коммутативность
умножения.
4. 
— ассоциативность
умножения.
5. 
— дистрибутивность
или распределительный закон.
Свойства комплексно-сопряженных чисел (без доказательств):
6. 
.
7. 
.
8. 
.
9. 
.
10. 
;
.
1.3. Комплексная плоскость
Рассмотрим
плоскость с декартовой прямоугольной
системой координат
.
Каждому комплексному числу
можно поставить в соответствие точку
плоскости
(см. рис. 1), причем это соответствие
взаимно однозначное. Плоскость, на
которой реализовано такое соответствие,
называется комплексной
п
лоскостью.
Так
как на оси
располагаются чисто вещественные числа
,
то она называется вещественной
осью. На оси
располагаются чисто мнимые числа
,
и эта ось называется мнимой
осью.
Иногда
удобнее сопоставлять комплексное число
не с точкой плоскости
,
а с радиусом-вектором
этой точки, т.е. с вектором, который
соединяет начало координат с рассматриваемой
точкой. В этом случае можно говорить о
модуле
комплексного числа, равном модулю
вектора
:
.
(1.1)
Из
свойств комплексно-сопряженных чисел
получаем:
.
Угол, образованный осью и вектором , называется аргументом комплексного числа z и обозначается
,
где
.
Отметим,
что для
аргумент не определен.
Очевидно,
что величина аргумента комплексного
числа
определяется неоднозначно. Наименьшее
по модулю значение аргумента называется
его главным
значением
и обозначается
.
Таким образом, имеем
;
,
.
Для аргумента комплексного числа с учетом следующих равенств:
;
;
,
где
. (1.2)
Отсюда получим
.