2. Кодирование информационных сигналов

2.1. Необходимость кодирования информационных сигналов

Во всех стандартах сотовой связи используют избыточное кодирование информационных сигналов при их передаче по радиоканалам. Это обусловлено нестабильностью параметров каналов в результате быстрых медленных замираний, что может приводить к появлению ошибок при приеме. Для индикации ошибок и их исправления и используют защитное избыточное кодирование.

Обнаружение ошибок осуществляют с помощью достаточно простых блочных кодов, например, путем проверки на четность. Следующая, более важная и сложная ступень задачи кодирования – выявление ошибок и их исправление. Для ее выполнения в системах подвижной связи в первую очередь применяют сверточные коды. Использование сверточных кодов требует наличия мощных быстродействующих процессоров. Сверточные коды хорошо исправляют случайные единичные или сдвоенные ошибки, но бесполезны при пакетах ошибок. Поэтому сверточное кодирование совмещают с перемежением информационных символов.

Блочные коды, исправляющие ошибки, также требуют при декодировании мощных вычислительных средств. При этом такие коды, как коды Файра и Рида-Соломона, способны исправлять пакеты ошибок. При передаче сигнализации часто используют каскадное кодирование. К внутреннему сверточному кодированию добавляют внешнее с исправлением пакетов ошибок. Разумеется, такое сложное кодирование требует большой избыточности, что формально снижает эффективность использования каналов, но существенно увеличивает достоверность принимаемой информации. Избыточность передаваемой информации определяют по скорости кода: R_кода = n_инф/n_код, где n_инф – число кодируемых информационных бит, а n_код – число бит после кодирования. Чем ниже скорость кода, тем большая кодовая защита принята в канале, но тем меньше скорость передачи информации при фиксированной скорости передачи в канале. При R_кода = 1 кодовая защита отсутствует.

В публикациях по обработке информационных и управляющих сигналов в системах подвижной связи часто говорят о кодировании, употребляя термин "предкоррекции” передаваемой информации". В традиционной радиотехнике под предкоррекцией понимают предыскажения, компенсирующие искажения в канале передачи. Применительно к задачам кодирования речь идет о статистической предкоррекции сигнала, когда известны лишь статистические свойства канала, вносящего ошибки. Кодированию подвергают типовые единицы передачи информации: кадры или блоки.

2. Блочное кодирование

В блочных кодах (БК) кодирование информации производят поблочно, в группах определенного числа бит (блоке). При этом, как правило, к к информационным символам добавляют проверочные символы (символы паритета), определяющие избыточность кода. Длина кодового слова с символами паритета составляет п символов. Такой метод кодирования называют систематическим, а соответствующие ему БК систематическими.

Теория и математическое описание БК базируются на использовании аппарата высшей алгебры, в частности полей Галуа GF(q). Размерность поля q определяет конечное число состояний, используемых для описания структур блоков. Так, поле GF(2) с двумя возможными состояниями 0 и 1 применяют при анализе двоичных кодов, где каждый символ информационного и кодового слов представляет один бит. В недвоичных кодах символ включает в себя несколько бит. Например, GF{16) с 16 возможными состояниями используют для описания кодов, где каждый символ состоит из четырех бит.

В основе блочного кодирования лежит понятие "расстояния по Хэммингу". Закодированное слово – это вектор длиной n, где к информационному вектору длиной k добавлены n-k проверочных бит (в частном случае, бит паритета). "Расстояние по Хэммингу" - это мера разницы между двумя кодовыми словами C_i и C_i в (n,k). Расстояние по Хэммингу равно числу ненулевых бит в выражении C_i + C_i в GF(2), где знаком "+" обозначена операция сложения по модулю 2. Так, если исходные слова C_i и C_i отличаются в одном бите, то после кодирования разница между ними может составлять 3, 5, 7 и более бит.

По назначению блочные коды подразделяют на проверочные коды (например, CRC – Check Redundancy Code) и коды, исправляющие ошибки.

Информационный блок можно представить вектором i, и к нему добавляют проверочную часть – вектор b = iP, где Р – порождающая матрица. Эту операцию можно представить в матричном виде (пример матрицы случайный):

(2.1)

Здесь i и b – матрицы-строки информационной и проверочной частей. Необходимо, чтобы все столбцы матрицы P были линейно независимы.

Используя формальную запись

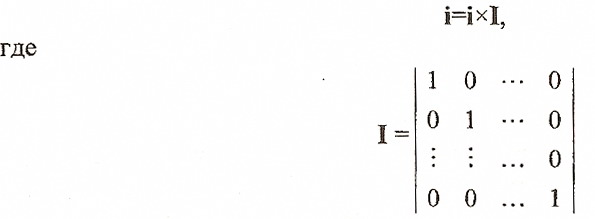(2.2)

единичная диагональная матрица k-го порядка и объединяя (суммируя) левые и правые части (2.1) и (2.2), получаем матричную форму записи кодового слова систематического кода:

c = i + b = i  G,

где G=[I P] называют порождающей матрицей систематического кода. Она имеет размер [kn].

При декодировании принятого кодового слова используют проверочную матpицу H размера [(n-k)n], удовлетворяющую условию ортогональности,

GH^т=0, (2.3)

где т – символ транспонирования.

Если при прохождении по каналу связи в кодовом слове с появятся ошибки, так что принятое слово w=с+e, где e – вектор ошибок, то, выполняя при декодировании операцию

wH^т = (с+e)H^т = iG H^т + eH^т = eH^т , (2.4)

получаем вектор синдрома s = wH^т = eH^т длиной (n–k), зависящий только от вектора ошибок и проверочной матрицы. Если ошибки отсутствуют, то s = 0.

Остановимся на методах исправления ошибок. Наиболее простой, но самый затратный метод – сравнить принятый вектор w со всеми возможными векторами с, соответствующим информационным словам i. Тот вектор, который по Хэммингу минимально отличается от принятого вектора w, считаем верным результатом.

Процесс поиска можно пояснить с помощью двумерной модели на плоскости (рис. 2.1). Каждое кодовое слово – точка в n-мерном пространстве. Минимальное расстояние по Хэммингу d_min определяют как минимум расстояния по всем возможным парам различных слов.

Рис. 2.1. К определению корректирующей способности кода

Корректирующая способность кода – это сфера, определяемая числом бит, которое может быть исправлено (радиус t на рис. 2.1). Общее число обнаруженных e_d и исправленных e_c ошибок подчиняется правилу

e_d + e_c ≤ d_min – 1, причем e_c ≤ e_d .

Так, если кодовое расстояние d_min = 7, то можно обнаружить и исправить 3 ошибки (радиус t = 3). Можно построить код так, что будут обнаружены 4 ошибки, но исправлены только 2 (сузить радиус t). Во всяком случае, если в принятом слове будет более 4-х ошибок, то будет принят неверный результат, т.е. процесс декодирования – это всегда вероятностный процесс.

В расчете вероятности правильности принятого решения лежат методы статистической радиотехники, используемые при приеме двоичных сигналов в каналах с помехами, многолучевом приеме и т.п. Например, во многих случаях при приеме сигналов вида "0" – "1" можно использовать модель Гаусса, где плотность вероятности приема сигнала определенного уровня описывает зависимость вида:

В результате коэффициент ошибок BER (Bit Error Rate) оценивают по формуле

BER = ½ erfc ( ), где

erfc (n) =

Существует большое разнообразие блочных кодов, начиная от проверочных кодов (CRC – Check Redundancy Code) до кодов, исправляющих групповые ошибки. Пример такого кода – код Рида-Соломона 1-го рода, используемый в стандарте cdma2000 при передаче телефонии вверх (в фундаментальном канале от мобильной станции к базовой). Здесь при декодировании используют мягкое решение, основанное на нахождении корреляционной функции принятого сигнала и правильного кода. Каждые 6 бит информационного блока кодируют 64-битовым словом функции Уолша wal₀…. wal₆₃ (рис. 2.2)¹. При приеме сигнал подают на 64 коррелятора и правильный ответ определяют по максимуму полученных корреляционных функций.

При использовании жестких решений принятый сигнал квантуют (каждому биту присваивают значение или "0" или "1"), а затем проверяют синдром. Ошибки определяют по полученному синдрому. Например, код (8,5) позволяет найти и исправить одну ошибку при передаче 5-битового слова (табл. 2.1).

Таблица 2.1

Синдром	Вектор ошибки
000	00000
001	00001
010	00010
100	00100
011	01000
101	10000
110	11000
111	10010

Рис. 2.2. Функции Уолша

2.3. Сверточное кодирование.

Cверточное кодирование – основной способ избыточного кодирования в радиосетях. В сверточных кодах используют непрерывную последовательную обработку потока информационных символов. Кодер обладает памятью в том смысле, что символы на его выходе зависят не только от очередного фрагмента (символа) на его входе, но и от предыдущих символов.

Свёрточный код (СК) относится к числу непрерывных кодов. В общем случае при сверточном кодировании группу из к информационных бит в канале передачи заменяют на n выходных двоичных символов, при формировании которых используют (К-1) предшествующих групп информационных бит. Величину К называют длиной кодового ограничения. Таким образом, свёрточный код характеризуют 3 параметра (п,к,К). В системах подвижной связи широко используют СК, где к = 1, п = 2 или 3 (одному информационному биту соответствует 2 или 3 передаваемых символа), или k=2, n=3 (двум информационным битам соответствуют 3 передаваемых: символа). Отношение R_кода = k/n, характеризующее вносимую СК избыточность, называют скоростью кода. Для приведенных примеров СК скорости R_кода = 1/2, R_кода =1/3 и R_кода =2/3 соответственно. Большие скорости кода позволяют увеличить пропускную способность канала связи, однако снижение скорости R улучшает качество передачи, уменьшает коэффициент ошибок (BER) на выходе приемника. Произведение кхК равно числу информационных бит, участвующих в формировании п выходных символов СК.

Закон кодирования определяет п образующих полиномов q₁ ... q_n. Например, для кода (2,1,3) можно взять

q₁=1+z² , (2.5)

q₂=1+z+z² (2.6)

где + обозначает операцию сложения по модулю 2, а z - оператор задержки на i длительностей бита.

Рассмотрим как пример процесс СК последовательности из 5 бит C_i = 01101 по закону образующих полиномов (2.5) и (2.6). Каждому информационному биту C_i соответствуют 2 выходных символа: q₁ и q₂ , в формировании которых участвуют 2 предшествующих бита – C_i-1 , C_i-2 (К=3). При СК первого бита "предшествующие" биты принимают равными логическому нулю. Результат СК показан на рис.2.3. При кодировании каждого следующего бита информационный сигнал сдвигают на 1 бит вправо и повторяют процесс.

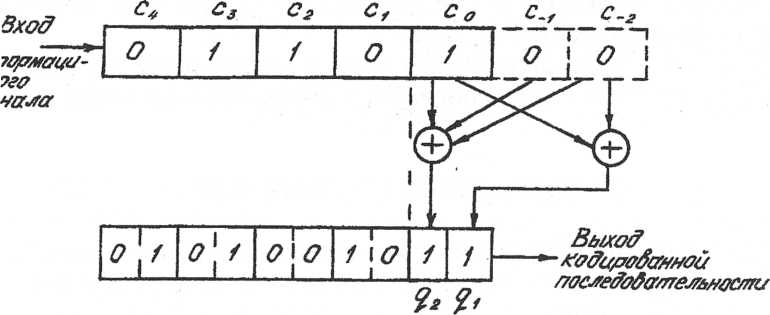
Рис. 2.3. Сверточный кодер (2,1,3)

Алгоритмы приема (декодирования) сигнала основаны на оценке его состояний в тактовые моменты времени. Под состоянием сигнала будем понимать отрезок информационного сигнала, состоящий из (К-1) х к информационных бит. При к = 1 каждое состояние характеризуют - текущий бит и (К-2) предшествующих бита. Всего при к = 1сигнал может принимать 2^K-1 состояний. В рассматриваемом примере СК (2,1,3) анализируют 4 возможных состояния сигнала: 00, 10, 01 и11. Переход из одного состояния в другое удобно представлять на диаграмме состояний сигнала (рис.2.4). При приходе следующего информационного бита возможны 2 перехода из каждого состояния в зависимости от того, равен следующий бит 1 или 0. Каждому пути (периоду) соответствует своя комбинация кодовых символом согласно (2.5) и (2.6).

Процесс декодирования сигнала, подвергнутого СК, состоит и определении оптимального пути от одного состояния к другому в соответствии с принятыми кодовыми символами q₁...._.q_n. Под оптимальным путем понимают путь, удовлетворяющий критерию максимального правдоподобия. Сегодня наиболее эффективным алгоритмом, позволяющим найти оптимальный путь, считают алгоритм Витерби, названный так по имени предложившего его А. Дж. Витерби. Идея алгоритма Витерби состоит в том, что в декодере воспроизводят все возможные пути последовательных изменений состояний сигнала, сопоставляя получаемые при этом кодовые символы q₁...._.q_n с принятыми аналогами по каналу связи и на основе анализа ошибок между принятыми и требуемыми символами определяют оптимальный путь.

Продемонстрируем работу алгоритма Витерби для рассматриваемого примера СК (2,1,3). Возьмем последовательность символов, полученную на рис.2.3, и будем полагать, что все символы q_i приняты без ошибок (рис. 2.5). Пояснения сопровождает графическое отображение изменений состояния сигнала на диаграмме (рис.2.6). Начальным всегда является состояние 00. В тактовый момент z=1 возможны два перехода: 00—>00, 00—>10. Первому переходу соответствует кодовая комбинация q₂q₁ = 00, второму  q₂q₁ = 11 (см. рис.2.4). Сравнение с принятыми q₂q₁ показывает, что первой ветви 00—>00 соответствуют две ошибки в приеме q₂q₁, а второй ветви 00—>10 нуль ошибок. Ошибка по каждой ветви служит метрикой d_H в смысле расстояния Хэмминга, т.е. соответствует числу отличающихся от требуемых принятых символов q₂q₁. Эти метрики зафиксированы в узлах диаграммы (рис.2.6).

Рис. 2.5. Принятая последовательность бит (на входе декодера)

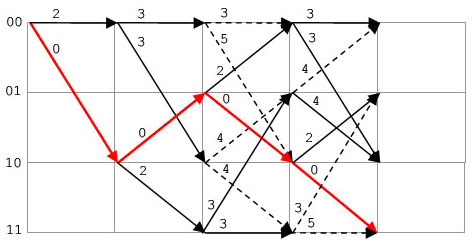
Рис. 2.6. Декодирование на основе диаграммы Витерби .При приеме

ошибки отсутствуют

В момент z = 2 сигнал может принять 4 состояния, которые определяются двумя возможными переходами из 00 и двумя переходами из 10. Сравнение с принятым q₂q₁ = 10 дает следующие метрики соответствующих ветвей d_H:

Суммарную метрику d_H по каждому из возможных путей определяем как сумму метрик составляющих его ветвей. Значения суммарных метрик показаны на диаграмме рис.2.6 для z = 2 и последующих моментов времени. Для момента времени z = 3 следует анализировать уже 8 возможных путей и сравнивать 8 соответствующих им метрик d_H . Алгоритм Витерби выбирает путь с наименьшей суммарной метрикой (штрафом) и начинает отбрасывать по ходу продвижения во времени те пути, которые имеют больший суммарный штраф в каждой точке диаграммы. Поэтому на каждом следующем этапе декодирования в рассматриваемом примере из 8 возможных путей остаются 4. Оптимальным путем является путь с наименьшим штрафом (при отсутствии ошибок в канале передачи символов d_H = 0). Последовательность бит на выходе декодера, соответствующая этому пути, совпадает с передаваемым информационным сигналом (рис.2.3).

Рассмотрим теперь случай, когда при передаче появились ошибки, например, во втором закодированном бите (рис. 2.7).

Рис. 2.7. Принятая последовательность бит (на входе декодера)

Теперь метрика первой ветви не равна нулю и суммарная метрика оптимального пути d_H = 1 (рис. 2.8). Однако, как следует из рис.2.8, оптимальный путь восстанавливает передачу последовательности информационных бит, т.е. использованный СК исправляет ошибки. Разумеется, алгоритм Витерби не во всех случаях дает верный результат на выходе декодера. Так, при двойной , а тем более тройной последовательной ошибке в передаче символов путь с наименьшей метрикой d_H содержит ошибку в одном бите на выходе при использовании данного кода.

Рис. 2.8. Декодирование на основе диаграммы Витерби .При приеме

есть одна ошибка

Двойные и тройные ошибки исправляют более мощные коды при использовании полиномов 4 и 6 порядков. При этом естественно увеличивается объем необходимых вычислений. При большем числе последовательных ошибок сверточные коды неэффективны. Поэтому перед передачей информацию в закодированных кадрах подвергают перемежению.

Рассмотренный метод декодирования, когда в качестве метрики используют расстояние Хэмминга, называют декодированием с жестким решением. Здесь каждому q_i на выходе демодулятора соответствует одно из двух значений: 0 или 1. Лучшие результаты в смысле восстановления исходного сигнала дает декодирование с мягким решением. В этом случае каждый символ на выходе демодулятора подвергают квантованию. Для оптимизации приема сигнала в канале с Гауссовым шумом достаточно использовать 8-уровневые квантователи. Каждому биту при приеме соответствует определенный вес. Чем больше этот вес, тем выше вероятность правильного приема. На рис. 2.9 и 2.10 рассмотрен вариант декодирования с мягким решением при отсутствии ошибок на входе, а на рис. 2.11 и 2.12 вариант с наличием ошибок.

Рис. 2.9. Принятая последовательность бит (на входе декодера)

Рис. 2.10. Декодирование на основе диаграммы Витерби .При приеме

ошибки отсутствуют

Рис. 2.11. Принятая последовательность бит (на входе декодера)

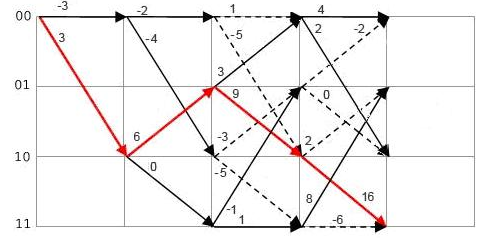
Рис. 2.12. Декодирование на основе диаграммы Витерби .При приеме

есть ошибка

На рис. 2.10 и 2.12 символы q₂q₁ представлены значениями с весовыми коэффициентами, а в узлах графа приведены соответствующие метрики. Из рис.2.10 следует, что при декодировании с мягким решением в качестве оптимального пути выбирают путь с максимальной суммарной метрикой, что соответствует максимальной накопленной доверительной вероятности. Более того, декодирование с мягким решением, производимое в примере на рис.2.10, 2.12, даже при трехкратной ошибке в приеме символов q_i может обеспечить оптимальный результат без ошибок на выходе декодера, что соответствует большей помехозащищенности канала связи, чем при использовании декодирования с жестким решением.

Рассмотренные примеры позволяют сделать ряд выводов об использовании алгоритма Витерби для декодирования СК. Прежде всего, выбор оптимального пути – это вероятностный процесс и всегда есть хотя бы ничтожно малая вероятность получить ошибочный результат. Вероятность получения правильного результата возрастает с увеличением размерности кода. Однако при этом растут требования к вычислительным способностям (быстродействию) процессора Витерби и объему памяти для хранения промежуточных результатов. На каждом следующем шаге общее число путей возрастает в 2 раза и на z-м шаге при к = 1 оно составит 2^Z+1 . Однако в процессе вычислений один из двух путей, сходящихся в один узел, отбрасывают, оставляя путь с наибольшим весом (наименьшим штрафом). Поэтому, начиная с z = K, всякий раз отбрасывают половину путей. Следовательно, алгоритм Витерби просчитывает на каждом этапе вычисления метрик не более 2^K путей.

Характеризуя различные сверточные коды, часто говорят об их мощности, понимая под этим способность кодов исправлять множественные, одиночные и многократные ошибки, возникающие в канале связи. Мощность кода зависит от длины кодового ограничения К и от вида образующих полиномов. Можно показать, что вероятность исправления ошибок при декодировании связана со свободным кодовым расстоянием d_f. Величину d_f определяют как кодовое расстояние по Хэммингу между правильным путем с нулевой метрикой (при приеме символов без ошибок) и ближайшим альтернативным путем (тоже с нулевой метрикой, но с ошибками на входе декодера и на его выходе). Так, для рассмотренного ранее в примере кода (2,1,3) с образующими полиномами q₂ и q₂ (2.5) и (2.6) величина d_f =5. Для кода (2,1,5) с образующими полиномами

q₁=1+z³+ z⁴ (2.7)

q₂=1+z+z³+z⁴, (2.8)

который используют при кодировании речевого сигнала в системе GSM, d_f=7. При декодировании с жестким решением допустимая кратность ошибок символов ограничена m_q< d_f /2. Следовательно, коды с большим кодовым ограничением К являются более мощными.

Высокая восстанавливающая способность СК позволяет применять на практике СК с перфорацией. Перфорация означает, что из последовательности символов на выходе кодера каждый р-й символ выбрасывают (не передают). При малом числе ошибок в приемнике неопределенность, возникающая из-за пропущенного символа, устраняют при вычислении метрик следующих ветвей для двух равновероятных значений пропущенного символа q_p = 0 и q_p = 1. При этом вероятность правильного приема снижается незначительно. В СК с перфорацией повышается скорость передачи. Так, перфорируя (выбрасывая) каждый четвертый символ в СК (2,1,3) или (2,1,5), повышают кодовую скорость с R_кода = 1/2 до R_кода = 2/3

Степень качества СК зависит от выбранного кода и характеристики канала передачи. Итоговую оценку производят по величине коэффициента ошибок (BER) при заданном отношении сигнал/шум в канале и типе канала. Поскольку СК хорошо исправляют одиночные ошибки, но чувствительны к пакетам ошибок, то их обычно применяют вместе с перемежением передаваемых по каналу символов.