Используя этот метод, решим задачу на построение сечения куба.

Задача №4.

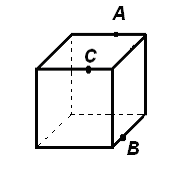
Построить сечение куба плоскостью, проходящей через три точки А, В, С, принадлежащие попарно скрещивающимся ребрам этого куба.

Слайды №14-15.

Решение:

Найдем пересечение прямой АВ, лежащей в плоскости сечения, с плоскостью основания куба. Для этого построим параллельные проекции А′, В′ точек А, В на основании куба в направлении бокового ребра куба.

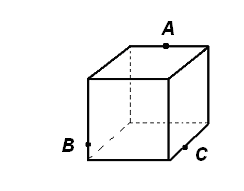
Пересечение прямых АВ и А′В′ будет искомой точкой Р. Она принадлежит плоскости сечения и плоскости основания куба. Следовательно, плоскость сечения пересекает основание куба по прямой СР.

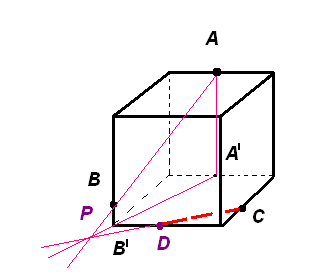
Точка пересечения этой прямой с ребром основания куба даст еще одну точку D сечения куба. Соединим точки С и D, B и D отрезками.

Через точку А проведем прямую, параллельную ВD, и точку ее пересечения с ребром кубам обозначим Е.

Соединим точки Е и С отрезком.

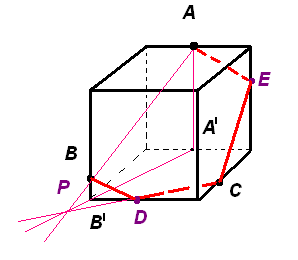
Через точку А проведем прямую, параллельную СD, и точку ее пересечения с ребром куба обозначим F.

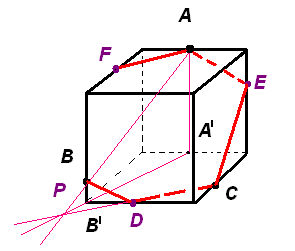
Соединим точки В и F отрезком.

Многоугольник AECDBF и будет искомым изображением сечения куба плоскостью.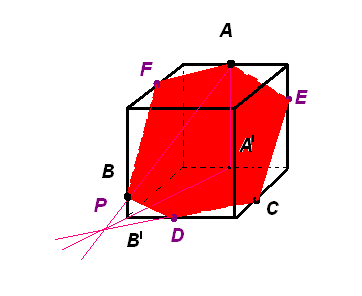

4. Закрепление изученного материала.

Самостоятельное решение задач с последующей проверкой.

Карточки.

Вариант 1 Какой фигурой является сечение куба А…D1 плоскостью, проходящей через вершины В1 и середину ребра СС1? Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

Вариант 2. Какой фигурой является сечение куба А…D1 плоскостью, проходящей через середины ребер АВ, ВС, и DD1? Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

5. Итог урока.

1. В каком случае в сечение куба получается треугольник?(равносторонний, равнобедренный, разносторонний)

2. Какие четырехугольники могут получится в сечении куба плоскостью?

3. Может ли в сечении куба плоскостью получится правильный пятиугольник? Почему?

4. В каком случае в сечении куба плоскостью получится правильный шестиугольник?

5. Может ли в сечении куба получится четырехугольник изображенный на рисунке?

Слайд №16.

6. В чем заключается построение сечений методом «следов»?

6. Домашнее задание.

Слайд №17

Решить задачу:

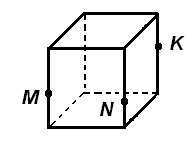
Построить сечение куба плоскостью проходящей через точки М, N, К.