Сценарий урока с использованием компьютера
Преподаватель – Сайнакова Расима Сайфулловна
Предмет – Геометрия
Тема – Построение сечений куба.
Продолжительность занятия — 80 минут
Класс — 10 класс
Образовательное учреждение — Томская область, Зырянский район, село Зырянское,
Муниципальная общеобразовательная школа № 2
Авторский медиапродукт - презентация 17 слайдов (среда Роwег Роint, Раint, Word).
МЕДИАПРОДУКТ
I. Среда: программа для создания презентаций Microsoft PowerPoint, графический редактор Рaint, текстовый редактор Мicrosoft Word.
II. Структура презентации:
№ п/п
|
СТРУКТУРНЫЕ ЭЛЕМЕНТЫ
|
ВРЕМЕННАЯ РЕАЛИЗАЦИЯ
|
№ КАДРА
|
1
|
Организационный момент
момент
|
3 МИНУТЫ
|
№1, №2
|
2
|
Актуализация знаний учащихся |
7 МИНУТ
|
№3
|
3
|
Изучение нового материала
материала
|
|
№4 -№15 |
|
Теория |
30 МИНУТ |
|
|
Практическое применение |
15 МИНУТ |
|
|
|
|
|
4 5 |
Закрепление изложенного материала
|
15 МИНУТ
|
|
5 |
Подведение итогов |
7 МИНУТ |
№16 |
6
|
Задание на дом
|
3 МИНУТЫ
|
№17
|
III. Схема взаимосвязи кадров презентации:
1
2
3
4
5
6
7
8
16
15
14
13
12
11
9
10
17
IV. Содержание кадров:
1. Тема урока.
2. Задачи урока.
3. Актуализация знаний учащихся.
4. Исследование возможных видов многоугольников получаемых в сечении куба. (Сечение куба в форме треугольника)
5. Доказательство невозможности получения сечения куба в форме прямоугольного и тупоугольного треугольника.
6. Какие четырехугольники могут получится в сечении куба?
7. Изображение сечения куба плоскостью в форме пятиугольника.
8. Сечение куба плоскостью в форме шестиугольника.
9. Вопрос о построении сечений куба. Задача.
10. Метод «следов». Определение .
Предварительные задачи на построение:
11. Задача №1.
12. Задача №2.
13. Задача №3.
14. Задача №4. Условие.
15. Задача №4. Решение.
16. Итог урока.
17. Задание на дом.
Целесообразность использования медиапродукта на занятии:
1 . недостаточное количество информационного материала в существующих учебно-методических пособиях (в учебниках нет определенных иллюстраций, схем, текстов и т.д.);
2. повышение эффективности усвоения учебного материала за счет одновременного изложения учителем необходимых сведений и показа демонстрационных фрагментов;
3. развитие наглядно-образного мышления за счет повышения уровня наглядности (виртуальное преобразование предметов в пространстве и на плоскости, виртуальный эксперимент- визуализация процессов, которые трудно или невозможно рассмотреть в реальных условиях и др.)
План занятия:
№ п/п
|
СТРУКТУРНЫЕ ЭЛЕМЕНТЫ
|
ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ
|
ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ
|
ВРЕМЕННАЯ РЕАЛИЗАЦИЯ
|
1
|
Организационный момент Целевая установка
|
Проверка готовности к уроку. Мотивация учащихся. Сообщение темы и разъяснение целей урока Сообщение темы и разъяснение целей урока
|
Восприятие разъяснений учителя
|
3 МИНУТЫ
|
2
|
Актуализация знаний учащихся |
Проверка знаний учащихся, полученных ранее
|
Устные ответы на вопросы учителя |
7 МИНУТЫ
|
3
|
Изучение нового материала
|
Лекция- беседа. |
Восприятие. Исследовательская работа. |
45 МИНУТ |
4 |
Закрепление изложенного материала
|
Наблюдение. Помощь по просьбе учащихся. |
Самостоятельная работа |
15 МИНУТ |
5 |
Подведение итогов |
Проверка усвоения материала. |
Ответы на вопросы. |
7 МИНУТ |
6 |
Задание на дом
|
Разъяснение задания на дом |
Запись в тетради задачи. Запись в дневники. |
3 МИНУТЫ |
Ход урока.
Организационный момент.
Сообщение темы и постановка цели и задач урока. (Слайд №1, №2)
Актуализация знаний учащихся.
Фронтальная работа с классом.(Слайд № 3)
Какая фигура называется кубом? (Куб –это параллелепипед, у которого все ребра равны )
перечислите вершины куба.
перечислите ребра куба.
перечислите грани куба.
назовите пары противоположных граней.
назовите основания куба.
назовите боковые грани куба.
Назовите пары прямых, определяемых вершинами этого куба, которые принадлежат одной плоскости.
Назовите пары скрещивающихся прямых, определяемых вершинами этого куба.
Изучение нового материала.
Исследование возможных видов многоугольников получаемых в сечении куба.
Учащимся раздаются карточки с изображением кубов.
1
.
2.
3. 4.
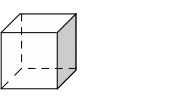
Выясним, какими могут быть сечения куба плоскостью.
На первом кубе отметьте точки А, В, С на ребрах исходящих из одной вершины.
Постройте сечение, проходящее через эти три точки.
Какая фигура получилась в плоскости сечения данного куба?
(треугольник)
Слайд №4.
- В каком случае в сечении получится равносторонний треугольник?
(В случае, если а = b = c)
- В каком случае треугольник в сечении получится равнобедренный?
(а = b или а = c, или b = с)
- В каком случае треугольник в сечении получится разносторонний?
(В случае, если а ≠ b ≠ c)
Может ли в сечении куба плоскостью получиться прямоугольный (тупоугольный) треугольник?
(нет)
Докажем, что в сечении куба плоскостью не может получиться прямоугольный (тупоугольный) треугольник.
Слайд №5.
Доказательство:
По теореме Пифагора :
АВ²
=а² + b²
АC² =а² + c² => АВ² < AC² + BC², => угол С острый.
ВC² =b² + c²
Аналогично углы А и В также острые, => ΔАВС – остроугольный.
II. Выясним какие четырехугольники могут получится в сечении куба плоскостью. (слайд №6)
Попробуйте изобразить сечение куба плоскостью в форме четырехугольника.
Учащиеся работают по карточкам, учитель следит за работой, после окончания работы просит нескольких учащихся изобразить свои сечения на доске.
Например, выбирают (если есть) такие сечения.
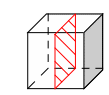
Какая закономерность прослеживается в построении этих сечений?
(сечения параллельны граням куба)
Какой четырехугольник получается в сечении в данном случае?
(квадрат)
Далее можно еще несколько учеников вызвать к доске, если среди их работ есть, например, следующие:
.
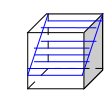
Если есть :
(плоскость сечения параллельна одному из ребер куба или проходит через ребро)
(прямоугольник)
|
Если нет:
(прямоугольник)
|
Далее можно еще несколько учеников вызвать к доске, если среди их работ есть, например, следующие:
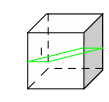
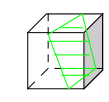
Если есть :
(плоскость сечения пересекает четыре параллельных ребра куба )
(параллелограмм)
|
Если нет:
(параллелограмм)
|