28.6. Порівняння складності факторизації rsa модулів перетворення

У ряді джерел [4, 5, 11–13, 421–425] запропоновано значне число моделей оцінки складності RSA криптоаналізу. Основним етапом криптоаналізу є факторизація модуля перетворення. У табл. 9.5 наведено аналітичні вирази, що можуть бути застосовані для оцінки експоненційної складності факторизації відповідних методів:

• метод перебирання типу «груба сила» зі складністю О(N^1/2);

• ρ-Полларда метод зі складністю О(N^1/4);

• P-1 Полларда метод;

• P+1 метод Вільямса;

• метод квадратичних форм Шенкса зі складністю О(N^1/4);

• метод Лемана.

До субекспоненційних методів необхідно віднести:

• метод Діксона зі складністю L_N(1/2, 2 );

• метод безперервних дробів зі складністю L_N(1/2, );

• метод квадратичного решета зі складністю L_N(1/2, );

• метод еліптичних кривих зі складністю L_p(1/2, ), де P – найменше просте, яке ділить N;

• метод решета числового поля зі складністю L_N(1/3,(64/9)^1/3);

• метод спеціального решета числового поля зі складністю L_N(1/3,(32/9)^1/3).

Функція у загальному випадку має вигляд (9.14) або

L_N (γ, = О(exp ( ^γ (Ln(Ln (N)) ^{1- γ)}), (9.31)

=1,92.

Таблиця 9.5

Cкладність факторизації RSA

Назва методу	Складність методу
Перебирання типу груба сила	О(N1/2)
ρ-Полларда метод	О(N1/4)
Метод квадратичних форм Шенкса	О(N1/4)
Метод Діксона	LN(1/2, 2 )
Метод безперервних дробів	LN(1/2, )
Метод квадратичного решета	LN(1/2, );
Метод еліптичних кривих	Lp(1/2, )
Метод решета числового поля	LN(1/3,(64/9)1/3)
Метод спеціального решета числового поля	LN(1/3,(32/9)1/3)
Поліноміальний метод Чалмерса	lnm N, 4<m<5

Таким чином, при застосуванні квадратичного або загального решета числового поля складність факторизації RSA модуля має субекспоненційний характер. При цьому для факторизації модулів, величина яких перевершує 330–350 бітів, краще використовувати метод загального решета числового поля. Підтвердженням висловленого є дані, що наведені в таблицях 9.1 та 9.3. Також необхідно відзначити, що метод квадратичного решета є набагато простішим у реалізації та розумінні. Для розуміння практичної реалізації загального решета числового поля рекомендується ознайомитись з прикладами, які наведені в [424] та [425].

Додаток А

Поліноміальний метод факторизації Чалмерса

Метод факторизації Гордона Чалмерса викладено в роботі [421]. Його сутність полягає в такому. Число N, яке необхідно факторизувати, зводиться до системи числення з основою х до вигляду:

, (9.27)

де C_N – число простих дільників числа N. Далі число подається у вигляді

,

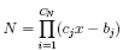або у нормованому вигляді

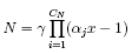. (9.28)

По суті, число N подається у вигляді рівняння, яке необхідно розв’язати. Дійсно, якщо підставити замість a_jx–1 значення p_j, то отримаємо

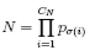, (9.29)

що і є канонічним розкладом числа N.

У [421] стверджується, що метод Чалмерса дозволяє здійснити факторизацію зі складністю

(ln N)^m (4.30)

кроків, де m, за твердженням автора, дорівнює приблизно 4 чи 5.

Метод Гордона Чалмерса має найменшу заявлену оцінку складності, однак на практиці для чисел, менше ніж 2⁷⁸⁰, він повільніший, ніж метод загального решета числового поля та метод квадратичного решета. Причина в тому, що надана автором в роботі [421] оцінка складності занижена. Крім того, обчисливши складність роботи алгоритму, легко переконатися, що навіть за умови, якщо оцінка ln^m N, 4<m<5 є точною, для малих чисел метод Гордона Чалмерса повільніший.

Дослідження впливу чисел спеціального вигляду проводилося шляхом вимірів складності факторизації чисел із «сильними» простими співмножниками і порівняння отриманих результатів з результатами для чисел зі «слабкими» співмножниками та з числами вигляду PQ±1, які гарантовано мають у канонічному розкладі багато малих множників. При дослідженні впливу спеціального вигляду числа N встановлено, що для алгоритму не має значення, чи є співмножники «сильними» чи «слабкими» простими числами чи навіть складеними числами. У цьому – його відмінність від інших методів, у яких складність прямо залежить від вигляду числа.

Метод Гордона Чалмерса – один із найперспективніших і потребує подальшого вивчення. Метод має шляхи прискорення роботи, однак для цього необхідно дати точну оцінку складності та виявити, від чого вона залежить.

Оскільки (9.29) можна подати у вигляді рівняння aх²+bх+с=0, то важливим є розподіл значень дискримінанти рівняння aх²+bх+с=0 залежно від значення х. Він може мати значний вплив на складність обчислень, якщо правильно обрати точку, з якої починати перебір варіантів і напрямок перебору. Також, оскільки значення дискримінанти частково впорядковане, то можна пройти n однакових значень дискримінанти максимально за 2log₂n кроків методом половинного ділення.