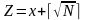28. 4. Метод факторизації «квадратичне решето»

До 1994 року для розкладання на множники застосовувався підхід, відомий як метод квадратичного решета [11, 236, 423, 422, 13, 425]. Загроза ключам великої довжини тут подвійна: безупинне зростання обчислювальної потужності сучасних комп’ютерів і безупинне вдосконалення алгоритмів розкладання на множники.

Розглянемо двійкове решето, яке, відповідно до сучасних поглядів, є найбільш швидким при довжині модуля не більше ніж 120 десяткових цифр.

Необхідно знайти два випадкові цілі числа x та y – такі, що:

. (9.6)

Представимо (9.6) у вигляді

. (9.7)

З урахуванням того, що в порівнянні (9.7) операції виконуються за модулем N, його

можна подати у вигляді рівняння:

, k=1,2,... (9.8)

Якщо розкласти (9.8) як різницю квадратів, то отримаємо, що

, k =1, 2, … . (9.9)

причому N = P×Q.

Вираз (9.9) доцільно застосовувати в таких випадках:

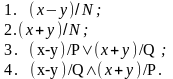(9.10)

У випадках 1 і 2 P або Q знайти не можна, оскільки модуль N не може бути розкладеним на співмножники. У випадках 3 та 4 маємо розв’язок.

Далі, якщо (х–у)/Р, то ми можемо скористатися алгоритмом Евкліда та обчислити найбільший спільний дільник:

(9.11)

Враховуючи (9.11), можна обчислити P або Q.

Практично факторизацію модуля N з використанням двійкового решета можна здійснити в такій послідовності.

1. Нехай N – число, яке необхідно факторизувати. Побудуємо деяку базу з таким значенням Z, щоб , де 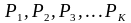– прості числа, краще невеликого розміру, Z – база двійкового решета.

2. Знайдемо 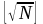, округливши знизу. Потім побудуємо числа вигляду

(9.12)

і знайдемо

.

Як результат отримаємо порівняння:

.

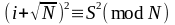Таким чином, маємо

. (9.13)

Приклад 9.3 [13]. Зловмисник визначив, що направлене шифрування виконується на відкритому ключі отримувача Е_к=31, модуль перетворення N=3599. Необхідно знайти особистий ключ отримувача D_k, з використанням якого можна здійснити розшифрування повідомлення М, якщо застосовується RSA перетворення.

Розв’язання задачі може здійснюватись у такому порядку:

1. Факторизуємо модуль N і визначаємо прості числа P та Q.

2. Знаходимо значення функції

.

3. Розв’язуємо порівняння

.

Факторизацію виконуємо, використовуючи метод двійкового решета.

Спочатку визначаємо базу розкладу – прості невеликі числа р₁, р₂,... р_r, добуток яких Р_б є близьким до N=3599:

.

Знаходимо

.

Будуємо таблицю 9.4.

Таблиця 9.4

Реалізація двійкового решета (розрахунки)

x		Z2mod3599	2	3	5	7	17	лишок
1	60	1	─	─	─	─	─	1
2	61	122	1	─	─	─	─	61
3	62	245	─	─	1	2	─	─
4	63	370	1	─	1	─	─	37
14	73	1730	1	─	1	─	─	173
23	82	3125	─	─	5	─	─	─
26	85	27	─	3	─	─	─	─
49	108	867	─	1	─	─	2	─
61	120	4	2	─	─	─	─	─
62	121	245	─	─	1	2	─	─

Беремо рядки зі значеннями x=3 та x=62, у результаті маємо, що:

;

.

Перемноживши рядки, маємо

або

.

Знайшовши залишок від значення 7502, маємо

.

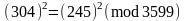Отже x=304, y=245.

Далі

НСД (│304-245│,3599)=59=Р,

= =61.

Отже, Р=59, Q=61.

Далі знаходимо

.

Тепер порівняння має такий вигляд:

.

Після переходу до рівняння

,

подамо його у вигляді:

.

Розв’язуємо це діафантове рівняння, використовуючи ланцюгові дроби:

; r0=112;

; r1=3;

; r2=1;

; r3=7; μ=3;

;

;

;

;

.

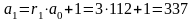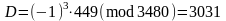Перевіримо правильність розв’язку:

.

Таким чином, E_k=31; D_k=3031.