24

Содержание

1. Шарнирно-рычажный механизм

1.1. Задание…………………………………………………………………………..

1.2. Кинематический анализ………………………………………………………..

1.3. Силовой анализ………………………………………………………………...

1.4. Определение уравновешивающего момента M_ур рычагом Жуковского….

2. Зубчатый механизм…………………………………………………………….

   0. 2.1. Задание………………………………………………………………………….

   1. 2.2. Синтез механизма……………………………………………………………....

   2. 2.3. Кинематический анализ ……………………………………………………….

Задание

Механизм управления рулем поворота.

Механизм предназначен для вращения руля поворота. Число расчетных точек 24. Аэродинамическая сила F_c3 приложена в точке S₃ и направлена горизонтально (0˚). Расстояние BS₂ принять равным l₂, а DS₃₌ l₃

1	Угол поворота звена DС		β	град.	22
2	Длина звена ВС		l2	м	3,6
3	Длина звена DС		l3	м	1,2
4	Угол крайнего положения		φ3min	град.	84
5	Частота вращения звена АВ		n1	об/мин	12
6	Масса звена ВС		m2	кг	32
7	Масса звена DС		m3	кг	220
8	Горизонтальная перегрузка		Пг	—	2.2
9	Момент трения в шарнире D		Мтр	Нм	220
10	Аэродинамическая сила при	φ3min	F'c3	Н	2300
		φ3cp	F΄΄c3	Н	44
		φ3max	F΄΄΄c3	Н	2300

1.2. Кинематический анализ

Кинематическое анализ состоит в изучении движения отдельных точек (звеньев) механизма независимо от сил, вызывающих это движение. Основной задачей кинематического анализа является определение:

1. положения всех звеньев при любом мгновенном положении ведущего звена;

2. траектории движения точек звеньев;

3. линейных скоростей и ускорений точек звеньев;

4. угловых скоростей и ускорений точек звеньев.

Существует три основных метода кинематического исследования механизмов:

графиков (наименее точный и наименее трудоемкий);

планов (более точный и более трудоемкий);

аналитический (самый точный и самый трудоемкий).

Графический метод, основанный на построении графиков законов движений с применением графического дифференцирования, обладает простотой и наглядностью, но имеет недостаточную точность, поэтому в инженерных расчетах применяют графоаналитический метод. Он дает удовлетворительную точность, но требует аккуратного выполнения графических работ и соблюдения масштаба.

Под масштабом подразумевается отношение действительной величины, выраженной в соответствующих единицах, к длине отрезка, изображающего эту величину, выраженной в миллиметрах. При построении кинематических схем и планов положений механизмов определяется масштаб длины, показывающий число метров натуральной величины, соответствующей одному миллиметру чертежа, м/мм:

, (2.6)

где – действительная длина кривошипа, м;

BC– длина отрезка, изображающего кривошип на чертеже, мм.

При построении планов скоростей и ускорений на чертеже приходится откладывать значения скорости и ускорения в некотором масштабе. Вектор вычисленной скорости точки , м/с, на плане скоростей изображен в виде отрезка произвольной длины, 73 мм, поделив значение скорости на длину этого отрезка, найдем масштаб плана скоростей, м/с  мм^-1:

(2.7)

Аналогично найдем масштаб плана ускорений, м/с  мм^-1:

м/с  мм^-1: (2.8)

где: а_B – вычисленное значение ускорения точки B, м/с²;

– масштабное значение ускорения точки А, мм.

Истинные значения скорости и ускорения любой точки механизма получают из их масштабных значений путем умножения последних на соответствующий масштаб.

Определение скоростей точек механизма методом планов скоростей:

Зная закон движения ведущего звена и длину каждого звена механизма, можно определить скорости его точек по значению и направлению в любом положении механизма путем построения плана скоростей для этого положения. Значения скоростей отдельных точек механизма необходимы при определении производительности и мощности машины, потерь на трение, кинематической энергии механизма; при расчете на прочность и решении других динамических задач.

Построение планов скоростей и чтение их упрощаются при использовании свойств этих планов:

1) векторы, проходящие через полюс P_V, выражают абсолютные скорости точек механизма. Они всегда направлены от полюса. В конце каждого вектора принято ставить малую букву a, b, c, ... или другую. Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе Р_V (О₁, О₂);

2) векторы, соединяющие концы векторов абсолютных скоростей, не проходящие через полюс, изображают относительные скорости. Направлены они всегда к той букве, которая стоит первой в обозначении скорости.

3) каждое подвижное звено механизма изображается на плане скоростей соответствующим одноименным, подобным и сходственно расположенным контуром, повернутым относительно схемы механизма на 90^° в сторону мгновенного вращения данного звена. Это свойство плана называется свойством подобия и позволяет легко находить скорость точек механизма.

Находим скорость точки B кривошипа О₁B по формуле, м/с:

V_B = ₁ ; V_B = 1,26  0,23 = 0.29 м/c (2.9)

Вектор направлен перпендикулярно к оси звена О₁B в сторону его вращения. Задаемся длиной отрезка ob (произвольно), который на плане будет изображать скорость точки B ; . Тогда масштаб плана скоростей, м/с  мм^-1,

м/с  мм^-1: (2.10)

Для дальнейшего построения плана скоростей и определения скорости точки C составляем уравнение:

; (2.11)

Для построения плана скоростей в расчетном положении механизма , из полюса проведена линия, перпендикулярная BA. В выбранном масштабе ( м/с,мм) на ней отложен отрезок _{,равный}

_(2.12)

_{Эквивалентный скорости}

Из точки p проведена линия , перпендикулярная СD, а из точки b линия , перпендикулярная СB. Их пересечение определяют точку С, а следовательно, и величину и _.

_(2.13)

_{Откуда :}

_{( 2.14)}

_{что близко к результатам аналитического расчета.}

Если вектор скорости мысленно перенести в точку С , то звено 2 будет вращаться по часовой стрелке, в силу чего в выражении для поставлен знак минус.

Определение ускорений точек механизма методом планов ускорений:

При помощи планов ускорений можно найти ускорения любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться их свойствами. Свойства такие же, как и у планов скоростей, кроме третьего, где фигура, подобная одноименной жесткой фигуре на плане положений механизма, повернута на угол (180 – ) в сторону мгновенного ускорения  данного звена,

где . (2.15)

Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.

Считая известными ускорения шарнирных точек (а_О = а_О = 0), помещаем их на плане ускорений в полюсе р_a. Звено AB вращается равномерно, поэтому точка B имеет только нормальное ускорение , которое направлено по звену BА к центру вращения О₁ (см.). Определяем его по формуле, м/с² :

(2.16)

Принимаем (произвольно) длину отрезка , изображающего вектор ускорения точки А, равной 72.5 мм. Тогда масштаб плана ускорений, м/с²мм^-,

; м/с²мм, (2.17)

Из полюса плана р_b откладываем параллельно звену AB в направлении от B к A.

Рассматривая движения точки C со звеном BC, составляем векторное уравнение:

(2.18)

Нормальные составляющие ускорений известны по значению и направлению. Их величины равны.

; (2.19)

Где и - где скорости соответствующих точек, определенные из

плана скоростей. По направление ускорения , , совпадают соответственно со звеньями СD,AB,CB и направлены к центрам вращения звеньев.

Для построения плана ускорений.

Из точки р плана ускорений параллельно звену АВ в направлении от точки В к точке А откладываем вектор , изображающий ускорение а_Вⁿ _, величина которого:

(2.20)

Отсюда аналогично. Из точки р плана ускорений параллельно звену BC в направлении от C к D откладываем вектор , изображающий ускорение а_Cⁿ, величина которого:

(2.21)

Аналогично из точки проводим линию , параллельную BC, на которой отложим отрезок эквивалентный ускорению Величина этого отрезка равна

_(2.22)

Из точек и проводим линии, перпендикулярные соответственно BC и СD.Их пересечение определяет точку и , а отрезок полное ускорение и . Отсюда ускорения равны.

_(2.23)

Из подобия треугольников найдем величины ускорений центров тяжести звеньев S₂, S_3, м/с²:

(2.24)

Определение угловых скоростей звеньев:

Угловое ускорение ₁ ведущего звена, совершающего равномерное движение, равно нулю.

Угловое ускорение звена 2-3 с^-2 ,

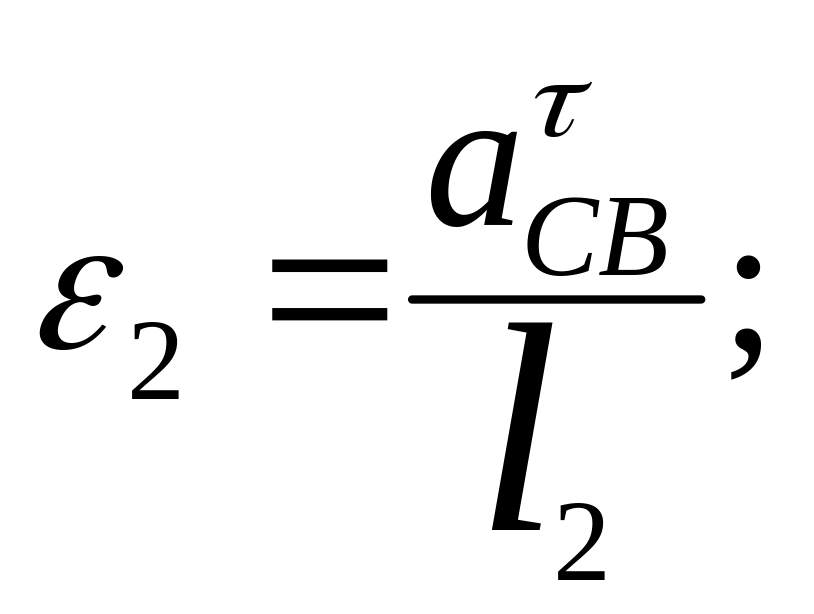
с^-2 (2.25)

с^-2

Для определения направления углового ускорения ₂ звена 2 надо мысленно перенести вектор тангенциального ускорения в точку С.

В направлении этого вектора точка B вращается относительно точки С против часовой стрелки. Знак плюс. По аналогии определяем значение и направление углового ускорения звена 3 :