2.2 Решение задачи №2

Рассмотрим трехфазную цепь с симметричным генератором и симметричной нагрузкой, в которой произошло короткое замыкание фаз А и С на землю (рисунок 2.2.1).

Рисунок 2.2.1

Исходные данные:

Решение:

Составим три однофазные схемы замещения и преобразуем их к простейшему виду.

Схема прямой последовательности (рисунок 2.2.2)

Рисунок 2.2.2

Схема обратной последовательности (рисунок 2.2.3)

Рисунок 2.2.3

Схема нулевой последовательности (рисунок 2.2.4)

Рисунок 2.2.4

Рассчитаем эквивалентные ЭДС и сопротивления

Эквивалентная ЭДС

Эквивалентные сопротивления ветвей

Составим систему шести уравнений: три – по законам Кирхгофа, три – по условиям в месте к.з. ( , , ):

Решив данную систему уравнений в системе MathCAD, получил следующие результаты:

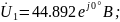
Определим токи и напряжения в месте короткого замыкания с помощью матрицы Фортескью:

Токи в месте короткого замыкания:

Решив данное выражение в системе MathCAD, получим следующие результаты:

Напряжения в месте короткого замыкания

Решив данное выражение в системе MathCAD, получим следующие результаты:

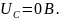
Построение вектороной диаграммы токов в месте короткого замыкания (рисунок 2.2.5)

Рисунок 2.2.5

Построение векторной диаграммы напряжений в месте короткого замыкания (рисунок 2.2.6)

Рисунок 2.2.6

2.3 Решение задачи №3

Проведем расчет линейной электрической цепи. Схема и кривая несинусоидальной ЭДС приложенной к цепи показаны на рисунке 2.3.1. Разложение функции в ряд Фурье в MathCAD приведён в приложении А.

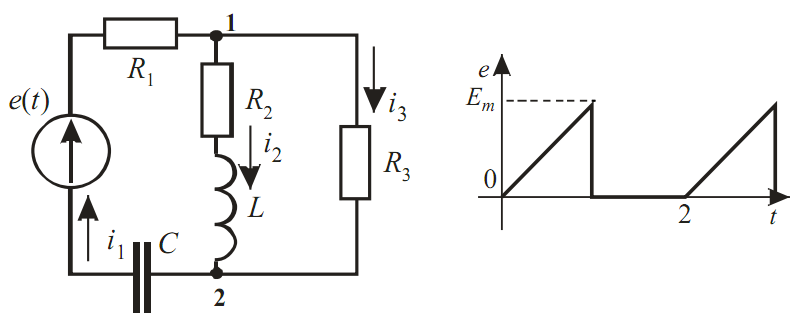
Рисунок 2.3.1

Значения параметров:

R₁=9 Ом; R₂=10 Ом; R₃=10 Ом; T=1.6*10^-2 c;

L=24 мГн; C=45 мкФ; E_m=320 B.

Представим ЭДС источника, заданную графически, рядом Фурье, ограничив число членов ряда постоянной составляющей и тремя первыми значимыми гармоническими составляющими:

e(t)=80+120.749sin(t+327.518º)+50.93sin(2t+180º)+34.709sin(3t+348.019º)+

+25.465sin(4t+180º)+20.536sin(5t+352.744º) B.

Построим графики спектров амплитуд и начальных фаз ЭДС источника, рисунок 2.3.2

Рисунок 2.3.2

Приближенное действующее значение ЭДС:

На рисунке 2.3.3 показана заданная кривая несинусоидальной ЭДС и кривая, полученная в результате сложения постоянной составляющей и первых пяти гармонических составляющих ряда. Построение осуществлено в среде MathCad.

Рисунок 2.3.3

Расчёт токов в ветвях проводим для каждой составляющей спектра по отдельности:

а) первая (основная) гармоническая составляющая:

e₁(t)=120.749sin(t+327.518) B

перейдем к комплексному амплитудному значению ЭДС:

Комплексные сопротивления ветвей:

Комплексные амплитуды токов ветвей на первой гармонике:

Мгновенные значения токов в ветвях на первой гармонике:

i₁₁(t)=0.34sin(t – 92.262) A

i₁₂(t)=0.169sin(t - 96.729) A

i₁₃(t)=0.171sin(t -87.849) A

Баланс мощностей:

Векторная диаграмма токов на первой гармонике:

Рисунок 2.3.4

б) вторая гармоническая составляющая:

e₂(t)=50,93sin(2t+180) B

перейдем к комплексному амплитудному значению ЭДС:

Комплексные сопротивления ветвей:

Комплексные амплитуды токов ветвей на второй гармонике:

Мгновенные значения токов в ветвях на второй гармонике:

i₂₁(t)=0.287sin(2t - 94.56) A

i₂₂(t)=0.142sin(2t -103.441) A

i₂₃(t)=0.145sin(2t -86.087) A

Баланс мощностей:

Векторная диаграмма токов на второй гармонике:

Рисунок 2.3.5

в) третья гармоническая составляющая:

e₃(t)=34,709sin(3t+348,019) B

перейдем к комплексному амплитудному значению ЭДС:

Комплексные сопротивления ветвей:

Комплексные амплитуды токов ветвей на второй гармонике:

Мгновенные значения токов в ветвях на третьей гармонике:

i₃₁(t)=0.293sin(3t - 96.925) A

i₃₂(t)=0.143sin(3t -110.116) A

i₃₃(t)=0.158sin(3t -85.001) A

Баланс мощностей:

Векторная диаграмма токов на третьей гармонике:

Рисунок 2.3.6

г) четвертая гармоническая составляющая:

e₄(t)=25,465sin(4t+180) B

перейдем к комплексному амплитудному значению ЭДС:

Комплексные сопротивления ветвей:

Комплексные амплитуды токов ветвей на четвертой гармонике:

Мгновенные значения токов в ветвях на четвёртой гармонике:

i₄₁(t)=0.287sin(4t – 99.378) A

i₄₂(t)=0.137sin(4t – 116.732) A

i₄₃(t)=0.162sin(4t – 84.726) A

Баланс мощностей:

Векторная диаграмма токов на четвертой гармонике:

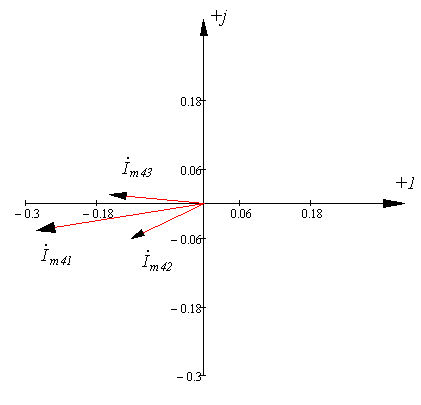
Рисунок 2.3.7

д) пятая гармоническая составляющая:

e₅(t)=20,536sin(5t+352,744) B

перейдем к комплексному амплитудному значению ЭДС:

Комплексные сопротивления ветвей:

Комплексные амплитуды токов ветвей на пятой гармонике:

Мгновенные значения токов в ветвях на пятой гармонике:

i₅₁(t)=0.289sin(5t – 101.927) A

i₅₂(t)=0.135sin(5t – 123.263) A

i₅₃(t)=0.171sin(5t – 85.265) A

Баланс мощностей:

Векторная диаграмма токов на пятой гармонике:

Рисунок 2.3.8

Используя метод наложения, запишем мгновенные токи ветвей:

i₁(t)=i₁₁(t) + i₂₁(t) + i₃₁(t) + i₄₁(t) + i₅₁(t) = 0.34sin(t – 92.262) + 0.287sin(2t – 94.56)+ 0.293sin(3t – 96.925) + 0.287sin(4t – 99.378) + 0.289sin(5t – 101.927), A

i₂(t)=i₁₁(t) + i₂₂(t) + i₃₂(t) + i₄₂(t) + i₅₂(t) = 0.169sin(t –96.729) + 0.142sin(2t – 103.441)+ 0.143sin(3t – 110.116) + 0.137sin(4t – 116.732) + 0.135sin(5t – 123.263) , A

i₃(t)=i₁₃(t) + i₂₃(t) + i₃₃(t) + i₄₃(t) + i₅₃(t) = 0.171sin(t – 87.849) + 0.148sin(2t – 86.087)+ 0.158sin(3t – 85.001) + 0.162sin(4t – 84.726) + 0.171sin(5t – 85.265) , A

Действующие значения токов ветвей:

Для определения мощности искажения определим полную мощность, активную и реактивную мощности всей цепи.

Полная мощность

S=E×I₁= 127.435 × 0.294 = 60.227 BA;

Активная мощность

P = P₁ + P₂ + P₃ + P₄ + P₅ = 0.81+0.581+0.614+0.596+0.614=3.215 Вт;

Реактивная мощность

Q = Q₁ + Q­₂ + Q₃ + Q₄ + Q₅ = -20.494 – 7.28 – 5.056 – 3.609 – 2.908 = -39.347 , BAp;

Мощность искажения

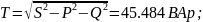
Коэффициент мощности