Методичні вказівки до виконання лабораторної роботи №4 “Розв’язування матричних ігор пакетом Scilab” з курсу “Теорія прийняття рішень” для студентів базового напрямку “Міжнародна інформація”

Теоретичні відомості

1.Розв’язування матричної гри в чистих стратегіях

Розглянемо математичну модель антагоністичної гри двох осіб с нульовою сумою. Гра складається з двох ходів: гравець А вибирає одну з можливих стратегій А_i, , а гравець В вибирає одну из можливих стратегій В_j, . Кожний вибір робиться при повному незнанні вибору суперника. В результаті виграш гравців складе відповідно a_ij і -a_ij. Ціль гравця А - максимізувати величину a_ij, а гравця В - мінімізувати цю величину.

Означення 1. Матриця, що складена з величин a_ij, , ,

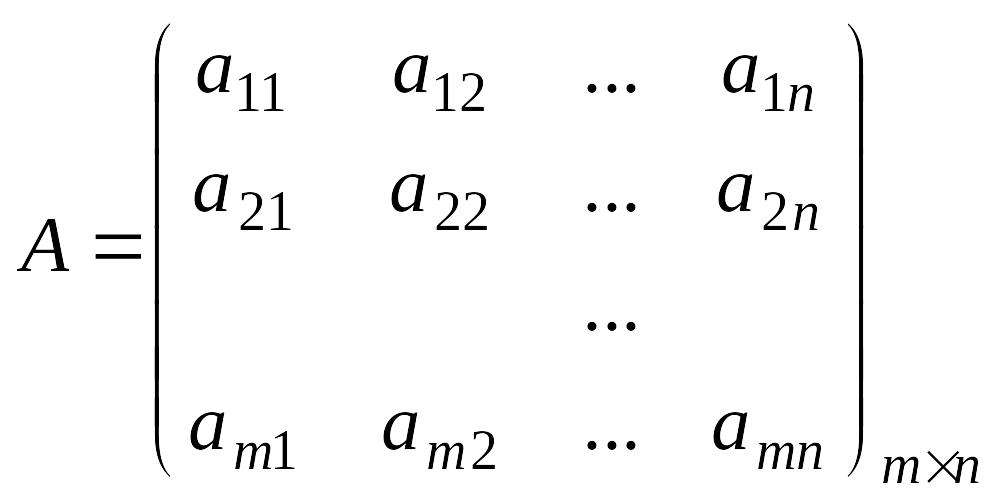
називається платіжною матрицею, або матрицею гри. Кожний елемент платіжної матриці a_ij, , дорівнює виграшу А (програшу В), якщо він вибрав стратегію А_i, , а гравець В вибирав стратегію В_j, .

Приклад. В грі беруть участь перщий и другий гравці, кожний з них може записати незалежно від іншого цифри 1, 2 і 3. Якщо різниця між цифрами, що записана гравцями, позитивна, то перший гравець виграє кількість очок, яка дорівнює різниці між цифрами, і, навпаки, якщо різниця від’ємна, то виграє другий гравець. Якщо різниця дорівнює нулеві, то гра закінчується нічьєю.

У першого гравця три стратегії (варіанти дії): А₁ (записати 1), А₂ (записати 2), А₃ (записати 3); у другого гравця також три стратегії: В₁, В₂, В₃ (див. таблицю).

	В1 = 1	В2 = 2	В3 = 3
А1 = 1	0	-1	-2
А2 = 2	1	0	-1
А3 = 3	2	1	0

Задача першого гравця - максимізувати свій виграш. Задача другого гравця - мінімізувати свій програш або мінімізувати виграш першого гравця. Платіжна матриця має вигляд

.

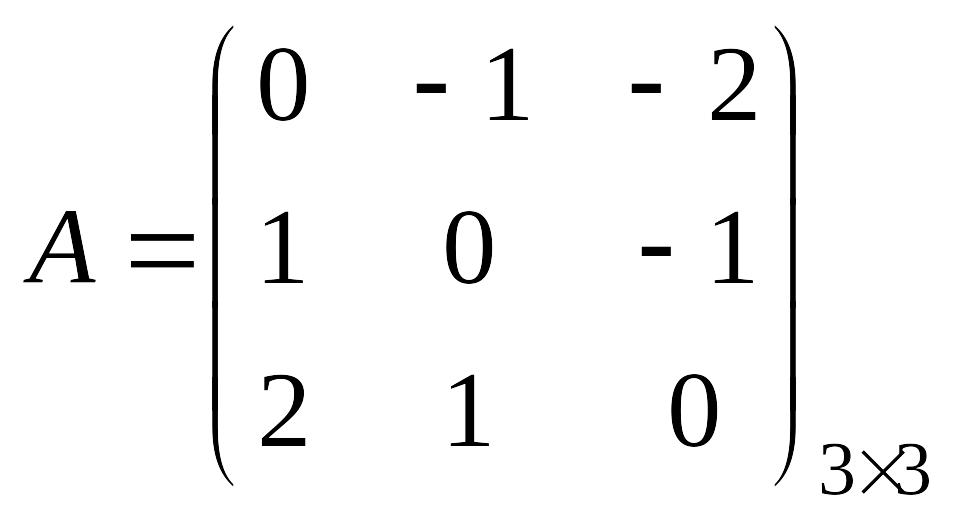Задача кожного з гравців – знайти найкращу стратегію гри, при цьому припускається, що противники однаково разумні та кожний з них робить все, щоб отримати найбільший дохід.

Знайдемо найкращу стратегію першого гравця. Якщо гравець А вибрав стратегію А_i, , то в гіршому випадку (наприклад, якщо його хід відомий В) він отримає виграш . Передбачаючи таку можливість, гравець А повинен вибрати таку стратегію, щоб максимізувати свій мінімальний виграш.

.

Означення 2. Величина a - гарантований виграш гравця А називається нижньою ціною гри. Стратегія A_iопт, що забезпечує отримання виграшу a, називається максимінною.

Якщо перший гравець буде притримуватися своєї максимінної стратегії, то у нього є гарантія, що він у любому випадку виграє не меньше від a.

Аналогічно визначається найкраща стратегія другого гравця. Гравець В при виборі стратегії В_j, в гіршому випадку отримає програш . Він вибирає стратегію B_jопт, при якій його програш будет мінімальним и складе

.

Означення 3. Величина b - гарантований програш гравця В називається верхньою ціною гри. Стратегія B_jопт, що забезпечує отримання програша b, називається мінімаксною.

Якщо другий гравець буде притримуватися своєї мінімаксної стратегії, то у нього є гарантія, що він в любому випадку програє не більше ніж b.

Фактичний виграш гравця А (програш гравця В) при разумних діях партнерів обмежений верхньою і нижньою цінами гри. Для матричної гри справедлива нерівність a £ b.

Означення 4. Якщо a = b =v, тобто

= ,

то виграш гравця А (програш гравця В) визначається числом v. Воно називається ціною гри.

Означення 5. Якщо a = b =v, то така гра називається грою з сідловою точкою, элемент матриці а_{iопт jопт} = v, що відповідає парі оптимальних стратегій (A_iопт, B_jопт), називається сідловою точкою матриці. Цей елемент є ціною гри.

Сідловій точці відповідають оптимальні стратегиї гравців. Їх сукупність – розв’язок гри, який володіє властивістю: якщо один із гравців придержується оптимальної стратегії, то другому відхилення від своєї оптимальної стратегії не може бути вигідним.

Означення 6. Якщо гра має сідлову точку, то кажуть, що вона розв’язується в чистих стратегіях.

Знайдемо розв’язок гри розглядуваного вище прикладу:

,

a = a₃ - нижня ціна гри.

,

b = b₃ - верхня ціна гри.

Так як a = b = 0, то матриця гри має сідлову точку.

Оптимальна стратегія першого гравця – А₃ , другого - B₃. З таблиці видно, що відхилення першого гравця від оптимальної стратегиї зменшує його виграш, а відхилення другого гравця від В₃ збільшує його програш.

Наявність сідловой точки в грі – це далеко не правило, скоріше, виключення. Існує разновидність ігор, які завжди мають сідлову точку і, значить, розв’язуються в чистих стратегіях. Цо так звані ігри з повною інформацією.

Означення 7. Грою з повною інформацією називається така гра, в якій кожний гравець при кожному особистому ході знає всю передісторію її развитку, тобто результати всіх попередніх ходів.

Прикладами ігор з повною інформацією можуть служити шашки, шахмати, "хрестики-ноліки" тощо.