3.Автокорреляция.

Следующим этапом в проверке спецификации ошибок является изучение сериальной корреляции. Автокоррелированность ошибок обычно возникает вследствие неправильной спецификации модели, например, при невключении в модель существенной объясняющей переменной с выраженной автокорреляцией, что приводит к негативным последствиям. Так, в случае положительной автокоррелированности ошибок, стандартные оценки дисперсий случайных величин оказываются заниженными, а при отрицательной – завышенными.

Проведем краткий графический анализ и посмотрим на зависимость остатков от номеров наблюдений. Если наблюдаются серии остатков, имеющих одинаковые знаки, то это характерно для моделей, в которых имеется положительная автокоррелированность ошибок. Если же знак остатков чередуется – то, скорее всего, есть отрицательная коррелированность ошибок.

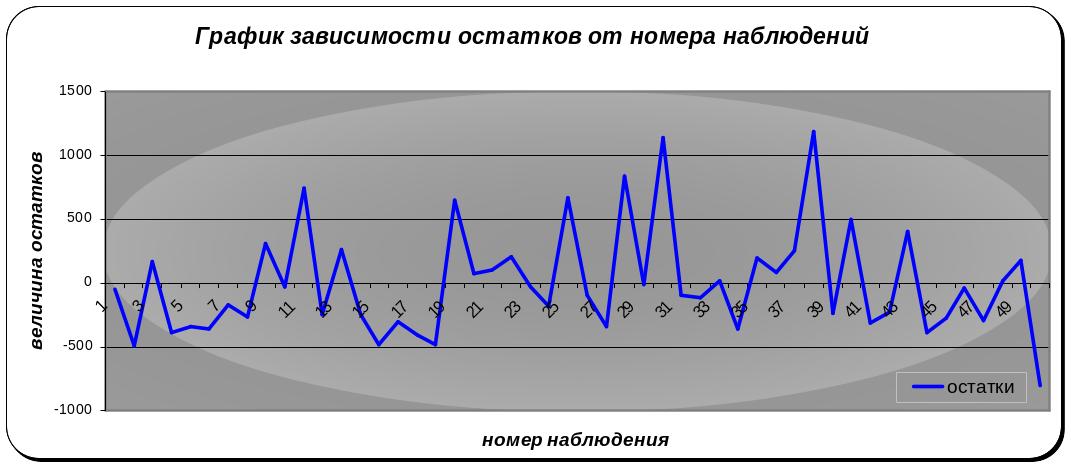
Рисунок 7 График проверка остатков на автокорреляцию

Данный график не дает четкой картины о наличии или отсутствии автокорреляции и о ее знаке, т.к. одновременно присутствуют «зубчатые» перепады и «волны» с одинаковым знаком.

Для точного определения автокорреляции воспользуемся следующими тестами: Бокса-Пирса, Льюинга-Бокса, z-тест, Дарбина-Уотсона и Бреуша-Годфри.

Большинство тестов исследуют идею: если корреляция есть у ошибок, то она присутствует и в остатках, получаемых после применения к модели обычного метода наименьших квадратов. Автокорреляционная функция имеет следующий вид: , где t=1,2…n. Выдвигается следующая гипотеза: Н₀ : p(m)=0.

Наиболее широко используется тест Дарбина –Уотсона, который основан на статистике :

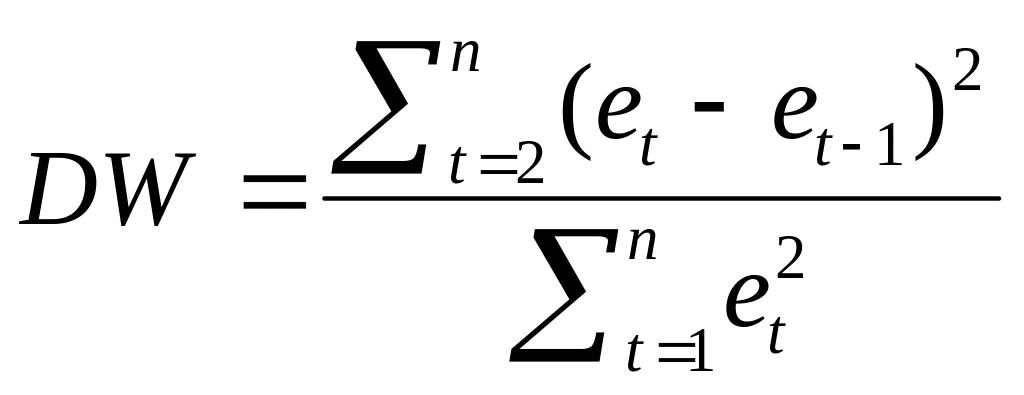, в данном случае – первый порядок. При этом считается, что постоянный член включен в число регрессоров. Тогда, проводя элементарные преобразования, не трудно заметить, что эта статистика тесно связанна с выборочным коэффициентом корреляции между и ,а именно: DW ~ 2(1-r). Отсюда следует что, если в остатках существует полная положительная автокорреляция и r = 1, то DW = 0. Если в остатках полная отрицательная автокорреляция, то r = – 1 и, следовательно, DW = 4. Если автокорреляция остатков отсутствует, то r = 0 и d = 2. Следовательно, 0 < DW< 4. Однако, чтобы понять отвергается или принимается первоначальная гипотеза – знать значение статистики DW недостаточно. Специфичность данного теста заключается в необходимости определения границ du – верхней и dl –нижней, что можно сделать с помощью специальной таблицы. Тогда: если (4-dl < DW < 4) ,то нулевая гипотеза отвергается и есть отрицательная корреляция, если (0 < DW < dl) – есть положительная корреляция, а если (du < DW < 4-du), то гипотеза не отвергается. Так же есть ситуации неопределенности: (4-du < DW < 4-dl) и (dl < DW < du), то есть, нет оснований для того, чтобы принять или отвергнуть гипотезу. Схематично можно изобразить следующим способом:

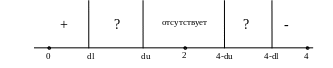
Рисунок 8 Правило определения гипотезы Дарбина-Уотсона

Наконец, после разбора спецификации метода, можем проверить нашу модель на присутствие автокорреляции. Для данной задачи DW = 2,12, нижняя граница dl=1,36, а верхняя граница du=1,4¹. Тогда, (4-du =2,6 > DW > du ), то есть гипотеза от отсутствии автокорреляции принимается на уровне значимости 0,05.

Проверим полученный вывод с помощью теста Бреуша-Годфри. Практическое применение теста также заключается в оценивании методом наименьших квадратов, однако по сравнению с тестом Дарбина-Уотсона, тест Бреуша- Годфри имеет весомые преимущества: во-первых, нет зоны неопределенности, а, во-вторых, в число регрессоров могут входить остатки не только с 1 лагом, но и 2,3 и т.д , что позволит выявить корреляцию не только между соседними, но и между более отдаленными переменными.

Исследуется модель: . Нулевая гипотеза выглядит следующим образом: .

В нашем случае была рассмотрена авторегрессионная зависимость остатков от их предыдущих значений с помощью модели 3-ого порядка.. Применяя МНК, получили следующее: . Ни один из коэффициентов при e_t-m незначим, P-значения соответственно равны 0,43 , 0,1 и 0,29. Однако все же рассчитаем статистику X²_набл =nR² . Критическое значение X²_крит =7,81 , что явно больше наблюдаемого (4,22). То есть, гипотеза об отсутствии автокорреляции до третьего порядка включительно принимается на уровне значимости 0.05.

Проведем еще несколько тестов² на автокорреляцию. Нулевая гипотеза остается той же. Данные занесем в таблицу для наглядности:

Таким образом, все проведенные тесты указывают на отсутствие автокорреляции, что можно объяснить совершенными знаниями о причинах и взаимосвязях, определяющих то или иное значение стоимости полиса автострахования КАСКО.