6.Проверка линейности регрессии.

В предыдущих главах мы определили наилучшую модель с двумя значимыми факторами - х₃-стоимость автомобиля и х₆ - стаж наименее опытного водителя. Теперь проверим линейность регрессии. Самый простой способ тестировать справедливость линейной спецификации модели – это добавить в правую часть нелинейные члены и тестировать их значимость. Воспользуемся RESET-тестом, который заключается в следующем: если модель верна, то добавление нелинейных переменных не должно помогать объяснять y. В частности, можно добавлять степени: .То есть выдвигается гипотеза Н₀ о том , что: Используем статистику Фишера для сравнения «короткого» и «длинного» уравнения:

,

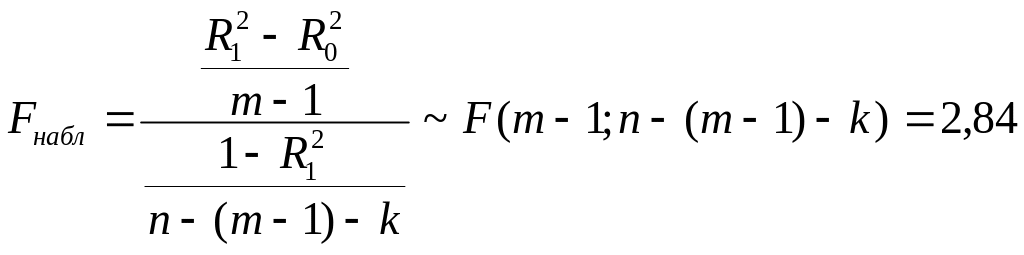где R²₀ – коэффициент детерминации короткой регрессии, который равен 0,8908, а R²₀ – коэффициент детерминации длинной регрессии, который равен 0,8909.

Т.к. наблюдаемое значение меньше критического (F_крит = 4,05), то гипотеза о линейности не отвергается на уровне значимости 0,05, вводить дополнительные нелинейные регрессоры не нужно. Заметим также, что все статистики значимы.

7.Регрессионная однородность выборки.

Далее, логично было бы проверить однородность нашей выборки. Исследуем, одинаково или нет различные группы водителей по стажу влияют на стоимость полиса КАСКО. С помощью Чоу-теста проверим, нужно ли рассматривать отдельно случаи, когда водитель за рулем меньше 5 лет и случаи, когда водитель обладает стажем больше 5 лет. То есть построим регрессионные уравнения по двум подвыборкам: , где х₆ от 0 до 5, и , где стаж больше 5.

Выдвигается следующая гипотеза: H₀ : , то есть не нужно разбивать выборку на подвыборки. Гипотеза проверяется на основе F статистики:

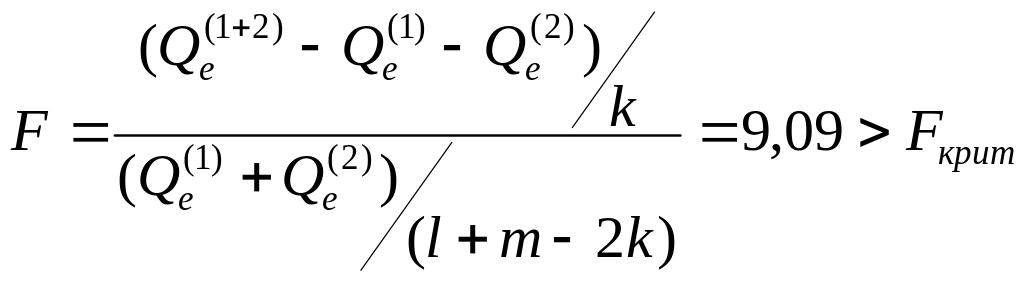. Коэффициент значим на уровне значимости 0,05.

На основе этого, можем сделать вывод о том, что первоначальная выборка неоднородна и юных и «опытных» водителей нужно рассматривать отдельно при изучении стоимости полиса автострахования каско.

Проверка спецификации ошибок.

1. Нормальность.

Как уже упоминалось в предыдущей главе, модель называется нормальной линейной регрессией в случае, когда ошибки имеют совместное нормальное распределение: То есть на данном этапе анализа необходимо проверить следующую гипотезу: H₀:

Сперва воспользуемся критерием Харке- Бера.

Если нулевая верна, то при достаточно больших выборках, статистика Харке-Бера (JB) имеет распределение, близкое к распределению Х² .

Если распределение ошибок действительно является нормальным, то значения выборочного коэффициента асимметрии (Аs) близки к нулю, а значения выборочного куртозиса (Кs) близко к трем. Поэтому гипотеза нормальности ошибок отвергается, если

значения этой статистики «слишком велики», т.е когда JB > X².

В данном случае:

, коэффициент асимметрии = 0,53, а куртозис 3,76.

Нулевая гипотеза принимается на уровне значимости 0,05, т.к JB < Х²_крит , который равен 5,99. Соответственно, если мы построим гистограмму остатков, то приближение к нормальному закону распределения не может остаться незамеченным.

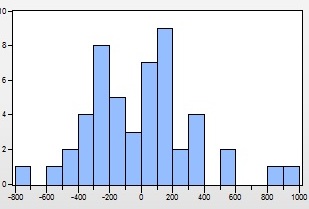
Рисунок 6 График остатков

Однако стоит заметить, что критерий Харке-бера является асимптиточеским, то есть распределение статистики JB приближается распределением Х²только при большом числе наблюдения n. Т.к. мы исследуем выборку все из 50 единиц, то следует проверить нормальность остатком и другими способами, для достоверности результатов.

По такому же принципу, проверим с помощью критерия Колмагорова-Смирнова и критерия согласия Пирсона выдвинутую ранее гипотезу о нормальном распределении ошибок, а результаты вычислений сведем в следующую таблицу для наглядности:

критерий	статистика	набл. зн.	крит. знач.	значимость
Колмогорова-Смирнова	D	0,112	0,895	0,050
Согласия Пирсона	X2	6,664	7,879	0,005

Таблица 15 Критерии на нормальнось

Как видно из таблицы, наблюдаемые значения статистик не превосходят критические, что говорит о нормальности распределения ошибок. Нулевая гипотеза не отвергается на уровне значимости 0,05 всеми тремя методами. Соответственно, модель - является нормальной линейной регрессией.