2. Исключение переменных.

Исключим из модели такой переменной, как возраст водителя- x(5), которой соответствует минимальное по модулю значение t-статистики |t₅|=-0,32 и для оставшихся переменных оценим уравнение регрессии с результатами в следующей таблице.

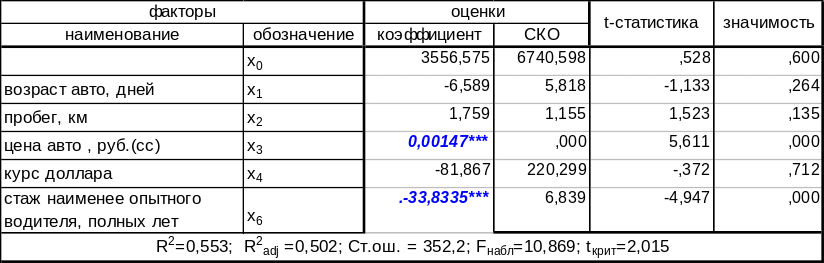
Таблица 3-коэффициенты регрессии (5 факторов)

По-прежнему на уровне значимости 0,001 значимы только коэффициенты при x (3) – цена автомобиля и x (6) – стаж наименее опытного водителя . Далее исключим из рассмотрения курс доллара - x (4), которому соответствует минимальное значение t-статистики по модулю = -0,372 и получим :

Таблица 4-коэффициент регрессии (4 фактора)

Теперь на уровне значимости 0,001 значимы не только коэффициенты при x(3) и x(5) , но и b₀ . Так же необходимо заметить, что по сравнению с предыдущими, в последней моделями увеличилось значение скорректированного коэффициента детерминации, которые показывает качество модели (используем именного этот показатель, так как он не зависит от размерности уравнении регрессии и мы можем сравнивать модели с разным количеством факторов) и снизилась стандартная ошибка. На следующем шаге исключим возраст автомобиля x(1), которому соответствует минимальное значение t-статистики = 1,159 :

Таблица 5-коэффициенты регрессии (3 фактора)

По-прежнему имеем три коэффициента, значимых на уровне 0,001.

Исключим x(2) – пробег автомобиля, т.к. при нем b₂- это единственный незначимый коэффициент.

Таблица 6-коэффициент регрессии (2 фактора)

Мы получили значимое уравнение регрессии со значимыми на уровне 0,001 и интерпретируемыми коэффициентами.

3. Включение переменных

На первом шаге в модель цены полиса КАСКО входит переменная x(3), за которой скрывается стоимость автомобиля. Выбор падает именно на нее из-за того, что она имеет самый высокий коэффициент корреляции со стоимостью полиса автостахования : r(y, x(3))=0,53

Таблица 7-коэффициенты регрессии (1 фактор)

На втором шаге, в соответствии с оценками парных коэффициентов корреляции включаем в уравнение наряду с x(3) переменные, как возраст водителя x(5) или стаж наименее опытного водителя x(6):

Таблица 8-коэффициенты регрессии (2 фактора – 3 и 6)

Таблица 9 коэффициенты регрессии (2 фактора – 3 и 5)

Сравнив таблицы 8 и 9, можно сделать вывод, что модель, в которой содержится стоимость автомобиля и стаж наименее опытного водителя - лучше, т.к. R²_adj больше, а стандартная ошибка – меньше.

Последующее включение переменных будет только ухудшать модель.

4. Проверка гипотез о линейном ограничении на параметры регрессии

Результат, полученный в предыдущем разделе подтверждается и при проверке гипотезы о включении переменных x1, x2, x4, x6 в уравнение. Следуя алгоритму проверки, рассчитывается «длинного» (с включением всех переменных) и «короткого» уравнения (без переменных, необходимость включения которых проверяется). Далее рассчитывается F-статистика:

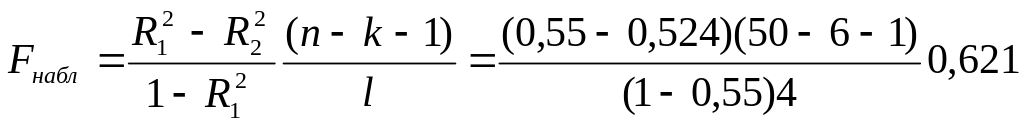и сравнивается с F критическим:

.

Так как < , гипотеза о незначимости факторов не отвергается, т.е. «короткое» уравнение лучше «длинного».

Итак, реализация алгоритмов пошагового исключения и пошагового включения привела к одному и тому же результату – модели, где в качестве объясняющих признаков использованы Х⁽³⁾ (цена автомобиля, руб.) и Х⁽⁶⁾ (стаж наименее опытного водителя, лет.).

Таблица 10 коэффициенты регрессии (2 фактора – 3 и 6)

Коэффициент ₀ в данном случае не имеет экономической интерпретации. Коэффициент ₃ показывает, что если стоимость автомобиля увеличится на 1 руб, то стоимость полиса КАСКО возрастет на 0,0015 долларов, а ₆ показывает, что при росте стажа водителя, который будет вписан в страховку на 1 год, стоимость полиса снижается на 32,88 доллара.