3. Параметры решетки, базис, координационное число

В общем случае элементарная ячейка кристаллической решетки представляет собой наклонный параллелепипед (рис. 8).

Если поместить начало координат в одну из вершин ячейки, то расстояния а,b,c до ближайших вершин и углы a, b, g между координатными осями называют параметрами кристаллической решетки.

Параметры a, b, c выражаются в ангстремах 1А=10^-8см (у металлов параметры решеток находятся в пределах 2-6 А.).

Базис решетки- это число атомов, приходящихся на одну элементарную ячейку.

В объемно центрированной ячейке всего 9 атомов ( 8 по вершинам куба и 1 в центре). Однако каждый из угловых атомов принадлежит данной ячейке только на 1/8, т.к. он одновременно принадлежит 8 соприкасающимся ячейкам. Поэтому на ячейку приходится (8 х 1/8) + 1 = 2 атома. Базис ОЦК - 2 атома.

В гранецентрированной ячейке всего 14 атомов ( 8 по вершинам куба и 6 в центрах боковых граней ). Каждый угловой атом принадлежит ячейке на 1/8, каждый центральный атом – на 1/2 . Поэтому базис ГЦК ( 8 х 1/8) + ( 6 х 1/2 ) = 4 атома.

В гексагональной плотноупакованной ячейке 17 атомов. На гпу ячейку

от 12 угловых атомов приходится только по 1/6 , от 2 атомов, лежащих в центрах оснований, - по 1/2, и только 3 атома, расположенные внутри ячейки, полностью принадлежат ей. Таким образом, базис ГПУ решетки - (12 х 1/6) + (2 х 1/2) + 3 = 6 атомов.

Кристаллическая решетка характеризуется также координационным числом К, которое показывает число атомов, расположенных на ближайшем одинаковом расстоянии от любого атома. Для ОЦК решетки К = 8, для ГЦК и ГПУ решеток К = 12. Чем выше координационное число, тем большая плотность упаковки атомов в ячейке.

1.4 Плотность упаковки атомов в решетке

При моделировании кристаллической решетки в виде соприкасающихся шаров между ними образуются пустоты.

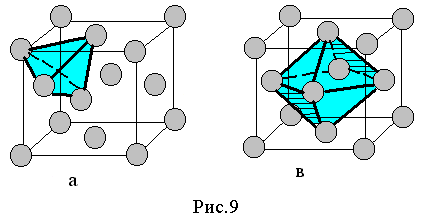
Так, например, три шара, прикрытые сверху одним шаром, образуют пустоту, называемую тетраэдрической (см. рис. 9,а), т. к. линии, соединяющие центры этих шаров, образуют тетраэдр. В тетраэдрическую пустоту можно вписать шар радиусом 0,22 R, где R - радиус шаров (атомов ячейки). Другой случай, когда три шара первого слоя прикрыты сверху не одним шаром, а треугольником из шаров, повернутым на 60⁰ относительно первого слоя. Пустоту, образованную шестью шарами, называют октаэдрической, т.к. линии, соединяющие центры этих шаров, образуют октаэдр (см. рис. 9, в). В нее можно вписать шар радиусом 0,41 R. На каждый шар приходится 1 эктаэдрическая и 2 тетраэдрические пустоты.

Наличие пустот в элементарной ячейке определяет плотность упаковки атомов в решетке. Плотностью упаковки называется отношение объема, занятого атомами, к объему ячейки. Так, плотность упаковки ОЦК равна 0,68, а упаковок ГЦК и ГПУ - 0,74.

2. Индексация плоскостей и направлений

в кристаллической решетке

2.1. Индексация плоскостей

Для обозначения плоскостей и направлений в кристаллической решетке используют индексы, связанные с координатными осями [3].

Для кубической решетки систему координат строят следующим образом. Начало координат помещают в одной из вершин элементарной ячейки, ось «х» направляют в сторону наблюдателя, ось «у» направляют горизонтально вправо и ось «z» - вертикально вверх.

Положение плоскости определяется отрезками, отсекаемыми ею на координатных осях. За единицу измерения вдоль каждой оси принимают параметр ( период ) решетки в направлении данной оси. Чтобы не иметь дело с бесконечностями, а также дробными числами, используют величины, обратные отрезкам, отсекаемым плоскостью на координатных осях, причем отношение этих величин приводят к отношению трех наименьших целых чисел. Совокупность таких чисел ( h,k,l ), заключенная в круглые скобки, называется индексами Миллера.

Индексы плоскости отыскиваются следующим образом. Определяются отрезки А, В и С, которые этой плоскостью отсекаются на осях координат.

Записываются величины, обратные отсекаемым отрезкам, например: 1/А, 1/В,1/С. Полученные дроби приводят к общему знаменателю, например,

это будет число D. Целые числа h = D / А, k = D / В, l = D / С и являются индексами данной плоскости.

Определим, например, индексы плоскости, которая отсекает на осях координат отрезки А = , В = 2 и С = . Отношения : : =

= . Общий знаменатель D = 2.

Индексами

плоскости являются величины h = , k = , l = .

Обозначение плоскости (416).

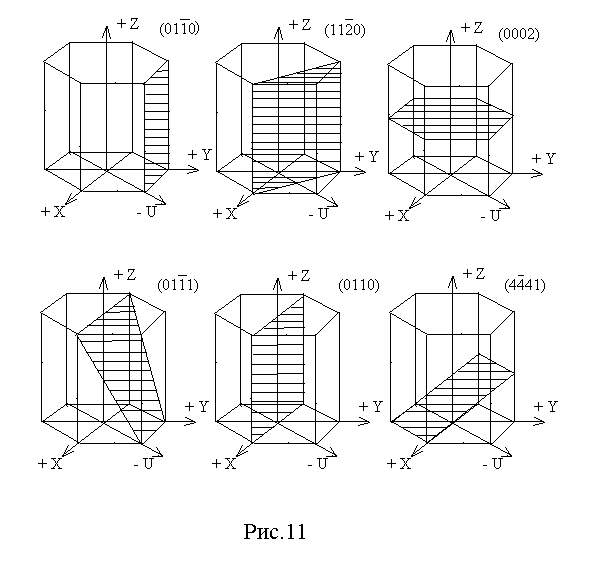
В гексагональной решетке начало координат помещают в центре основания ячейки и в плоскости основания проводят три координатные оси x, y, u, расположенные под 120⁰ и ось z вертикально вверх. Такая 4-х индексная система Миллера - Бравэ содержит четвертый индекс i, который ставят на третьем месте ( h, k, i, l ). Дополнительный индекс i вычисляется через индексы h и k: i = - ( h + k ). В случае, если отрезок отсекается плоскостью на отрицательном направлении координатной оси, то над соответствующим индексом ставится черта.

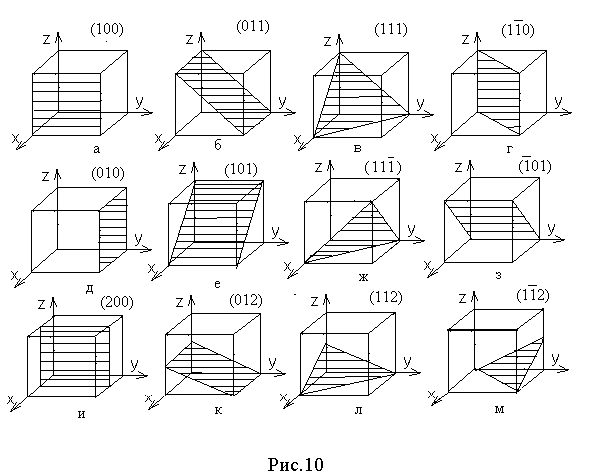
Примеры индексации плоскостей в кубической решетке показаны на рис. 10, а

в гексагональной плотноупакованной решетке – на рис. 11.

Непараллельные плоскости, имеющие одинаковое атомное строение (количество атомов и их расположение), кристаллографически эквивалентны.

Всю совокупность эквивалентных плоскостей обозначают индексом какой-либо одной плоскости, заключенным в фигурные скобки. Например, плоскости 100, 010, 001, 100, 010, 001. Их обозначают индексом одной какой-либо плоскости и заключают в фигурные скобки как семейство плоскостей 100 или 001. Другой пример, семейство 111. Это плоскости 111, 111,111, 111 и др. Если плоскость проходит через начало координат, то для удобства ее

индексации начало координат следует перенести в какую-либо соседнюю вершину элементарной ячейки.