8.2. Условие постоянства объема. Смещенный объем. Скорость деформации

Поскольку плотность металла в результате пластической деформации меняется незначительно, считается, что объем тела до деформации равен объему тела после деформации. В этом состоит закон постоянства объема.

Однако, в процессе деформации объем тела уменьшается, т. к. пластическая деформация всегда сопровождается упругой деформацией. После окончания деформации упругая деформация исчезает, и тело восстанавливает прежний объем. Зависимость упругой деформации от напряжения подчиняется закону Гука :  = Е.

А

Р На диаграмме «сила-деформация» (рис. 58):

К ОС - полная деформация при нагрузке Р,

ОВ - пластическая (остаточная) деформация после снятия нагрузки,

О В С  ВС - упругая деформация.

Рис.58

После снятия нагрузки длина растянутого образца уменьшается на величину упругой деформации ВС.

Величина tg  КОВ = tg  АВС называется модулем Юнга.

В большинстве операций обработки давлением при значительной пластической деформации упругой деформацией можно пренебрегать. Однако в ряде операций, например, при гибке вхолодную, упругую деформацию необходимо учитывать, задавая угол в инструменте (штампе) отличным на угол пружинения от требуемого угла готовой детали.

Рассмотрим тело до и после деформации (см. рис. 59).

Из равенства объемов

Z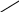 _и V = Х_д Y_д Z_д = X_и Y_и Z_и

Z_д следует :

Y_и Y_д

X_и X_д

Рис.59

После логарифмирования получим:

или _x + _y + _z = 0,

где _x = ln ; _y = ; _z = ln

Величины _x, _y, _z называются действительными или истинными степенями деформации.

Для оценки степени деформации можно пользоваться и другими величинами.

Относительные степени деформации: _x = ; _y = ; _z= ;

В обеих оценках положительной степени деформации соответствует растяжение, отрицательной - сжатие.

Величины  и  связаны между собой

.

Разложим выражение в ряд: _x = ln ( 1 + _x ) = _x - _x²/2 + _x³/3 - ...

Этот ряд при _x  1 - сходящийся. Отбросив все члены, кроме первого, получим _x  _x.

Для степеней деформации, меньших 0,1 (т. е. для малых деформаций) можно считать _x = _x.

Соответственно, _x + _y + _z = 0, т.к. _x + _y + _z = 0.

Умножив равенство на объем деформированного тела, получим для всех степеней деформации V_x+ V_y + V_z= 0,

а для малых степеней деформаций V_x +V_y +V_z = 0.

Произведения объема тела на степени деформации представляют собой смещенные объемы V_c по соответствующим направлениям. Таким образом, сумма смещенных объемов равна нулю: V_cx + V_cy + V_cz = 0.

Скоростью деформации называется изменение степени деформации в единицу времени или относительное смещение объема в единицу времени.

^ = d/dt = dV_с / Vdt.

Для малых степеней деформации ^ = d / dt.

При постоянной скорости , а также для средней скорости:

^ =  / t и ^ =  / t.

От скорости деформации следует отличать скорость деформирования (скорость движения деформирующего инструмента), а также скорость смещения тех или иных точек тела в процессе деформирования.

Рассмотрим растяжение двух образцов разной длины Z_и1 Z_и2 (рис. 60)

при одинаковой скорости деформирования, т.е. за одно и то же время зажи-

мы машины переместились на одно и то же расстояние Z. Z_д1 - Z_и1 = Z_д2 - Z_и2 = Z

Если промежуток времени t принять за единицу, то ^₁=  / t = Z / Z_и1·1,

^₂=  / t = Z / Z_и2·1 или 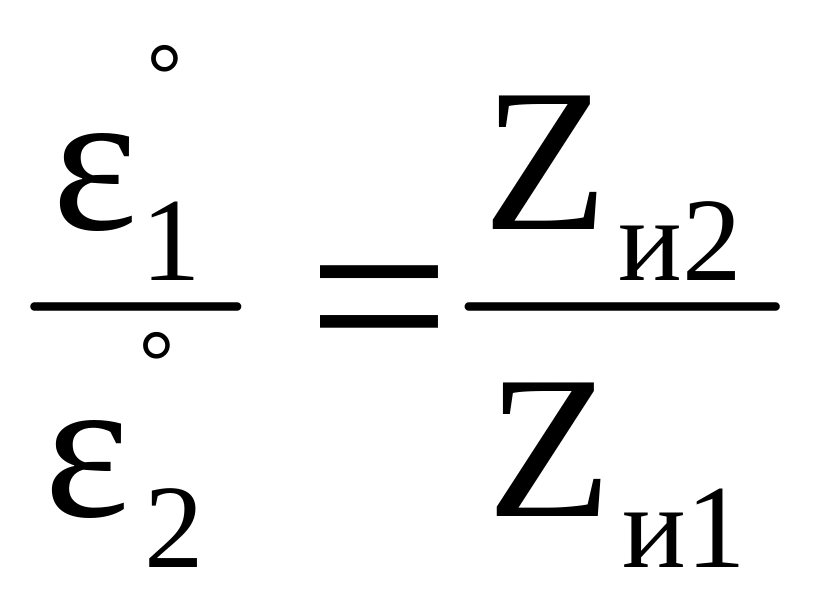, т. е. мы получили, что скорости деформации разные (при одинаковой скорости деформирования).

Если промежуток времени принят за единицу, имеем также:

V_деф = Z / t = Z / 1 = Z , откуда Z = V_деф

где V_деф – скорость деформирования.

Но из ^₁= Z / Z_и1·1, откуда Z = ^₁Z_и1 и тогда получаем зависимость между скоростью деформации, скоростью деформирования и размером образца: ^₁ = V_деф / Z_и1 и ^₂ = V_деф / Z_и2.

Скорости перемещения точек рассматриваемых тел изменяются по высоте образца линейно от нуля в месте закрепления до максимума на верхних торцовых плоскостях.

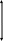
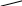
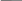
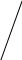
Z Z

Z_и1 Z_и2

Z_д1 Z_д2

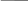Рис.60

Рассмотрим влияние скорости деформации на пластичность и сопротивление деформированию.

Обычно определение механических свойств металла проводят на испытательных машинах при скоростях деформирования порядка 10 мм/с.

Реальные технологические процессы проводят на прессах со скоростями 100-500 мм/с, а на молотах 5 - 10 м/с, т. е. скорости деформации и деформирования существенно выше, чем при испытаниях.

С увеличением скорости деформации напряжение текучести материала возрастает, а пластичность падает. При холодной деформации это влияние скорости на механические характеристики материала значительно ниже, чем при горячей обработке. Поэтому формулы, описывающие зависимость свойств от скорости деформации, разные для холодного и горячего деформирования.

При полном и неполном упрочнении, что соответствует холодной и неполной холодной деформации: .

При полном и неполном разупрочнении, что соответствует горячей и неполной горячей обработке: ,

где _s и _s0 - напряжения текучести соответственно при скоростях деформации ^ и ^₀, m и n - константы, определяемые экспериментально для различных материалов.