5.7. Контур и вектор Бюргерса

Одной из характеристик дислокации является вектор смещения - вектор Бюргерса. Вектор Бюргерса - это дополнительный вектор, который нужно ввести в контур, описанный вокруг дислокации, чтобы замкнуть соответствующий ему контур в решетке идеального кристалла, разомкнувшийся из-за наличия дислокации.

На рис.34 показан контур, проведенный в решетке идеального кристалла путем последовательного обхода некоторой зоны от атома к атому, причем число атомов на противоположных сторонах контура одинаково.

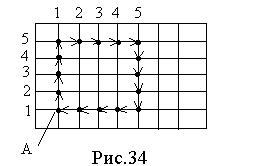
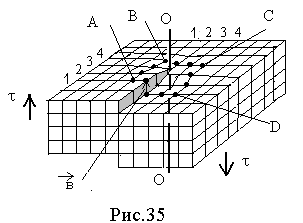
Теперь построим соответствующий контур, называемый контуром Бюр- герса, в искаженной решетке реального кристалла, например, вокруг винтовой дислокации, как показано на рис. 35, или вокруг краевой дислокации, как

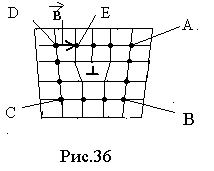
показано на рис. 36. Начинаем обход по часовой стрелки из точки А. Идем 4 шага, равных межатомному расстоянию, до точки В, затем 4 шага до точки С и 4 шага до точки D.

В обоих случаях для того, чтобы замкнуть контур в направлении от D к А, необходимо ввести дополнительный вектор в, который и называется вектором Бюргерса. У краевой дислокации вектор Бюргерса перпендикулярен, а у винтовой дислокации – параллелен линии дислокации.

Вектор Бюргерса является мерой искаженности кристаллической решетки, обусловленной присутствием в ней дислокации. Если дислокация вводится в кристалл чистым сдвигом, то вектор сдвига и является вектором Бюргерса.

Контур Бюргерса может быть смещен вдоль линии дислокации, растянут или сжат в направлении, перпендикулярном линии дислокации, при этом величина и направление вектора Бюргерса остаются постоянными.

5.8. Размножение дислокаций при пластическом

деформировании

Изначально дислокации возникают в процессе кристаллизации из расплава. Растущие из расплава зерна имеют различную ориентацию кристаллографических осей и поэтому при срастании зерен на их границах возникают нарушения правильности кристаллической решетки, т. е. дислокации. Поскольку общая протяженность границ зерен очень велика, количество дислокаций в них огромно. В реальном металле в отожженном состоянии на каждый 1 см² площади сечения приходится 10⁶ - 10⁸ дислокаций.

Рентгено-структурный анализ показывает, что после деформирования плотность дислокаций увеличивается на 3 - 4 порядка и составляет уже 10¹² дислокаций на 1 см². Это говорит о том, что в процессе деформации происходит зарождение новых дислокаций или попросту размножение исходных дислокаций. Каждая исходная дислокация является источником появления новых. Механизм генерирования дислокаций в процессе деформирования был открыт в 1950 г. английскими учеными Франком и Ридом. Для пояснения этого механизма рассмотрим процесс образования мыльных пузырей с помощью трубки (см. рис. 37). При смачивания конца трубки мыльным раствором на торце трубки образуется плоская пленка, закрывающая отверстие. При постепенном повышении давления воздуха в трубке пленка выпучивается, последовательно проходя стадии 1, 2, 3, 4

.

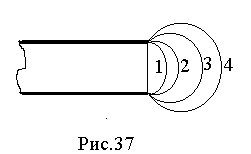
До тех пор, пока пленка не примет форму полусферы (стадия 2), ее состояние является неустойчивым: с уменьшением давления пленка сокращается, стремясь к исходному состоянию. После прохождения стадии 2 состояние пузыря меняется: он может развиваться не только при постоянном, но даже при уменьшающемся давлении до тех пор, пока не отделится от трубки, на конце которой снова появляется плоская пленка, и начинается формироваться второй пузырь, затем третий и т.д.

Теперь рассмотрим действие источника Франка-Рида. Представим линейную дислокацию, как закрепленную по краям нить (рис. 38).

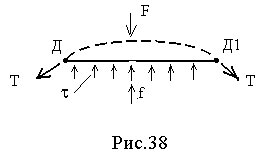
Поскольку все атомы взаимосвязаны силами взаимного притяжения, дислокация обладает определенным запасом упругой энергии, и поэтому дислокацию можно представить не просто, как нить, но как нить, упруго растянутую силами Т. Причиной закрепления линии дислокации в точках Д и Д₁ является встреча данной дислокации с уплотнением атомов в стенках, являющихся границами зерен, или с другими дислокациями, распространяющимися в других плоскостях скольжения.

На дислокацию действуют 2 силовых фактора. Первый - это внешняя сила f, вызывающая касательные напряжения сдвига  и растягивающая линию дислокации в дугу (при закрепленных концах). Второй - это внутренняя сила упругости нити F, стремящаяся восстановить первоначальную форму.

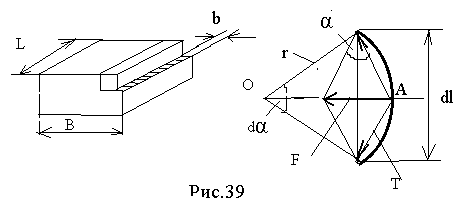
На рис. 39 показаны кристалл в форме параллелепипеда с размерами В и L, а также элементарный отрезок краевой дислокации длиной dl.

Касательные напряжения  от внешней силы распределены по поверхности площадью BL и при сдвиге на «b» производят работу А₁ =  BLb, где ВL - сила, b- перемещение, численно равное единичному сдвигу ( вектору Бюргерса).

Введем понятие единичной силы f , действующей на единицу длины дислокации. Тогда работа этой силы при полном пробеге дислокации на пути В будет а₂ = fB, а на всей длине дислокации А₂ = fBL. Приравнивая работы А₂ и а₂ , получим fBL = BLb . Отсюда f = b, т.е. сила, действующая на единицу длины дислокации, равна касательному напряжению, умноженному на вектор Бюргерса.

Это выражение справедливо для любой формы линии дислокации, причем единичная сила f перпендикулярна линии дислокации в любой ее точке.

Вернемся к схеме упругой нити. На элемент дуги dl действует сила f dl = bdl, направленная вдоль радиуса ОА. Противодействующая ей восстанавливающая сила F (результат линейного растяжения):

F = 2Tsin  2 T  Tdα.

Т.к. dα  , то F = T .

Сила Т линейного натяжения дислокации определяется следующим образом

(без вывода): Т = аGb²,

где G - модуль сдвига, коэффициент а = 0,5 - 1.

Тогда F =

Приравнивая силу от внешних напряжений и силу от натяжения дислокации, получим:

=bdl, откуда  =

Из этого соотношения определяется радиус дуги r , при котором приложенная сила уравновешивает восстанавливающую.

По мере роста касательного напряжения дуга все более выгибается, и радиус ее уменьшается. На рис. 40 показаны изменение формы дислокационной линии и направление действующих единичных сил f = b.

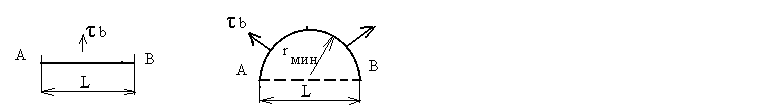
Рис.40

Как видно из формулы, максимальное касательное напряжение _мах достигается при минимальном радиусе r _мин дислокации. Минимальный радиус r_мин = , где L - длина линии дислокации. Таким образом, дуга дислокации становится полуокружностью.

При подстановке а = 0,5 и r = 0,5 L касательное напряжение становится максимальным (критическим ) и равным :  _кр = G b / L.

Видно, что критическое напряжение тем меньше, чем больше длина закрепленного отрезка дислокации. Если в эту формулу подставить типичные для отожженных монокристаллов G, b, L, то критическое напряжение _кр  0,1 кг/мм², что хорошо согласуется с его экспериментальными значениями.

Выгибание дуги от r = до r_кр = L / 2 требует непрерывного повышения касательного напряжения от 0 до _кр = Gb / L. После достижения _кр петля продолжает расширяться, но, будучи закрепленной в точках Д и Д₁, закручивается в этих точках в виде двух симметричных спиралей под действием силы «b», постоянно перпендикулярной линии дислокации на всех ее участках.

В некоторый момент спиралевидные участки дислокации в процессе закручивания соприкасаются между собой. В месте соприкосновения встречаются дислокации противоположного знака, которые взаимно уничтожаются и дислокация разделяется на две - замкнутую петлю и дислокацию ДСД₁ (см.рис.41). После этого, если продолжает действовать критическое напряжение, источник рассмотренным путем дает новую дислокационную петлю. Эти петли под действием касательного напряжения могут неограниченно распространяться во все стороны.

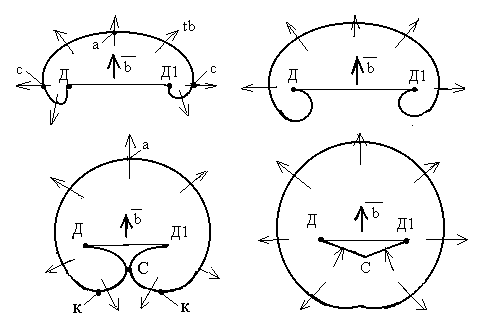
рис. 41

Если исходная дислокация была чисто краевой, то при выгибании ее в дугу она превращается в смешанную дислокацию. На рисунке вблизи точки «а» дислокация носит краевую ориентацию ( вектор b перпендикулярен линии дислокации). Вблизи точек «с» ориентация винтовая, т.к. вектор b параллелен линии дислокации. В промежуточных точках дислокация смешанная.

Поскольку вблизи точек «с» участки винтовой дислокации имеют противоположные знаки, то под действием одной и той же силы они движутся в противоположных направлениях, перпендикулярных вектору b. На участках вблизи точек «к» дислокации имеют краевую ориентацию, но знак их противоположен знаку краевой ориентации вблизи точки «а». Под действием одних и тех же сил краевые дислокации разного знака перемещаются в противоположных направлениях. Вблизи точки «С» дислокации снова винтовые и, как и вблизи точек «с», они имеют противоположные знаки, поэтому притягиваются. Образуется замкнутая петля. Дислокационная линия ДД в конце каждого цикла образования петли восстанавливается, поэтому она может генерировать неограниченное количество петель. Каждая петля при своем распространении на плоскости скольжения производит единичный сдвиг. Многократной генерацией и образованием большого количества петель объясняются перемещения в тысячи межатомных расстояний, наблюдающихся при пластической деформации кристалла.