18. Теория рядов.

18.1. Числовые ряды.

18.1.1. Основные определения. Пусть дана бесконечная числовая последовательность .

Числовым рядом называется составленная из членов этой последовательности запись

. (18.1.1)

Эквивалентная (18.1.1) форма записи ряда - с применением символа суммы: .

Числа называют членами ряда; , называется общим членом ряда. В результате вычисления значений этой функции при n=1, n=2, n=3, … должны получаться члены ряда .

Примеры. 1. Пусть . Записать ряд.

При n=1 получаем , при n=2 , при n=3 и т.д., ряд имеет вид .

2. Пусть ряд имеет вид 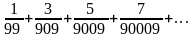. Придумать формулу общего члена.

Эта задача имеет много решений, мы придумаем одно из них. Числители растут линейно с n с шагом 2, поэтому в формуле для числителя должно содержаться 2n. Подбором убеждаемся, что для числителей верна формула 2n-1 (=1 при n =1, 3 при n =2 и т.д.). Также подбором убеждаемся, что для знаменателей можно взять формулу , поэтому . Если нумерацию членов ряда начать с n = 0, то .

Основным понятием теории рядов является понятие сходимости числового ряда. Пусть дан ряд (18.1.1). Составим из его членов конечные суммы, называемые частичными суммами ряда:

Определение. Если существует конечный предел S последовательности частичных сумм ряда (18.1.1) при , то говорят, что ряд сходится; число S называют суммой ряда и пишут или .

Если 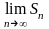не существует (в том числе бесконечен), ряд называется расходящимся.

Примеры. 1. Ряд 1+1+1+…+1+…, очевидно, расходится, так как .

2. Ряд 1-1+1-…+(-1)^n-1+… тоже расходится, так как и вообще а такая последовательность предела не имеет.

Дальше мы рассмотрим два ряда, к которым в той или иной мере будет сводиться большинство рядов: геометрическую прогрессию и гармонический ряд.

3. Геометрической прогрессией называется ряд . (18.1.2)

Число q называют знаменателем прогрессии. Сразу отметим, что при ряд расходится. При получаем ряд структуры, рассмотренной в примере 1, при - ряд структуры, рассмотренной в примере 2. Пусть теперь 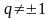. Выведем формулу для частичных сумм. Пусть , тогда . Легко убедиться, что . Решая это уравнение относительно , получим . В этом выражении от n зависит только , при этом Следовательно, конечный существует при , и . Итак, геометрическая прогрессия сходится, если её знаменатель удовлетворяет условию , и её сумма равна .

4. Гармоническим рядом называется ряд

. (18.1.3)

Докажем, что этот ряд расходится. Рассмотрим частичные суммы с числом слагаемых, равных степеням числа 2: .

Сумма членов в каждой скобке больше 1/2: , , и т.д. Таким образом, . Последовательность, у которой есть стремящаяся к бесконечности подпоследовательность, не может иметь конечного предела, поэтому гармонический ряд расходится.

В дальнейшем мы редко будем находить сумму ряда; в основном, будет ставиться вопрос о сходимости или расходимости ряда. Для вычисления суммы обычно применяются разложения в ряд элементарных функций, которые мы будем изучать дальше, или искусственные приёмы, например, разложения функции на простые слагаемые:

5. . Если общий член ряда представить в виде суммы простых слагаемых , то . Итак, этот ряд сходится, и его сумма равна 1.

18.1.2. Свойства сходящихся рядов.

18.1.2.1. Необходимый признак сходимости ряда. Общий член сходящегося ряда

(18.2.1)

стремится к нулю при : .

сходится . Обратное неверно. Пример – гармонический ряд.

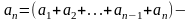
Доказательство. Если , то и , но , следовательно .

С проверки выполнения условия надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2) , однако этот ряд расходится.

Введём понятие остатка ряда.

Определение. Остатком ряда (18.2.1) после n-го члена называется ряд .

18.1.2.2. Если сходится ряд (18.2.1), то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.

Доказательство. Пусть - частичные суммы ряда (18.2.1); обозначим k-ую частичную сумму остатка : . Тогда 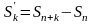. Устремим , считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный , следовательно существует конечный предел , т.е. остаток сходится. Обратное утверждение доказывается также. Так как , то из существования конечного предела следует существование конечного предела , т.е. из сходимости остатка следует сходимость ряда.

Житейский вывод из этого свойства: отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.

18.1.2.3. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при .

Доказательство. Пусть S - сумма исходного ряда (18.2.1), - сумма его остатка. Из равенства следует , т.е. . Отсюда .

Здесь тоже можно сделать житейский вывод. Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства , определяется пределом , т.е. началом ряда.

18.1.2.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.

Доказательство. Частичная сумма ряда есть ; по свойству предела .

18.1.2.5. Два сходящихся ряда и можно почленно складывать и вычитать; ряд также сходится, и его сумма равна .

Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм: .

18.1.3. Сходимость рядов с положительными членами (положительных рядов). Термином "положительный ряд" мы будем называть числовой ряд с неотрицательными членами: для . Для таких рядов частичная сумма является возрастающей функцией аргумента n. Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху, поэтому сразу сформулируем признак сходимости положительных рядов:

Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.

В случае, когда последовательность частичных сумм положительного ряда неограничена, будем говорить, что его сумма равна .

При доказательстве расходимости гармонического ряда мы, по существу, доказали, что последовательность его частичных сумм неограничена. В качестве другого примера прямого применения этого признака рассмотрим ряд Дирихле (или обобщённый гармонический ряд)

. (18.3.1)

Если s<1, то 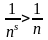, и, так как частичные суммы неограничены, то суммы и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2: …+ .

Структура каждой скобки: , поэтому (мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.

Итак, ряд Дирихле (18.3.1) сходится при s>1, расходится при s 1. Дальше мы дадим более простое доказательство этого факта, основанное на интегральном признаке Коши.