Методические указания к выполнению
лабораторной работы 5
Уменьшение случайной погрешности цифрового вольтметра
Цель работы
Изучить способ уменьшения случайной погрешности путем усреднения результатов наблюдений.
Экспериментально определить метрологические характеристики при усреднении результатов наблюдений.
Задание на работу
1. Экспериментально определить метрологические характеристики цифрового вольтметра:
Систематическую погрешность цифрового вольтметра
Предельные значения погрешности цифрового вольтметра
2. Исследовать зависимость погрешности измерения при усреднении от числа наблюдений.
Теоретические сведения
1 Метрологические характеристики цифровых измерительных устройств
Статическая характеристика преобразования. Эта характеристика ЦИУ устанавливает связь между преобразуемой (входной) величиной X и результатом преобразования, за который принимается значение Nq, где N - значение выходного кода, q - квант. Для идеального ЦИУ характеристика преобразования имеет вид показанный на рис. 1 и получена при квантовании путем отождествления с ближайшем уровнем квантования. Изменения значений кода идеального ЦИУ со значений N-1 на N происходят при фиксированных значениях входной величины равных (N-0,5)q, где N - целое число.
Статическая характеристика определяется значением единицы младшего разряда кода, равной кванту q . Значение и q может быть найдено при заданном диапазоне измерения (Xмin, Xmax), числе разрядов выходного кода n по формуле для АЦП q = (Xmax - Xмin -) / 2n или q = (Xmax - Xмin -) / 10n для цифрового прибора.
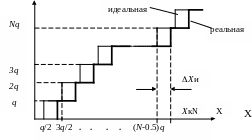
Рис. 1 Статическая характеристика преобразования ЦИУ
Статические погрешности циу. Абсолютное значение статической погрешности циу может быть определено по формуле
X = Xр - X = Nq - X,
где Xр= Nq – результат измерения, N - выходной код ЦИУ, q - квант, X – истинное значение измеряемой величины.
В соответствии с принятой классификацией погрешности делятся на отдельные составляющие. По причинам возникновения погрешности делятся на методические и инструментальные. К методическим погрешностям относят погрешности, обусловленные несовершенством принятого метода измерения (погрешность квантования по уровню), под инструментальными – погрешности обусловленные несовершенством технической реализации ЦИУ.
В зависимости от характера изменения погрешности по диапазону измерения СИ погрешности делятся на аддитивные и мультипликативные. Аддитивные погрешности не зависят от значения измеряемой величины X, мультипликативные растут с увеличением X. Обычно для CИ погрешность задается в виде модели
X = a + bX
где a и bX - аддитивная и мультипликативная составляющая погрешности соответственно.
По характеру изменения погрешности при повторных измерениях одного и того же значения погрешности делятся на систематические и случайные. Систематические остаются постоянными или меняются закономерным образом, значения случайных погрешностей можно предсказать с некоторой вероятностью. В общем случае погрешность является случайной величиной и ее можно представить в виде
X = Xсист + Xсл
где Xсист = M[X] – систематическая погрешность (математическое ожидание погрешности); Xсл – случайная составляющая погрешности.
Для
оценки значений погрешности как случайной
величины применяются характеристики:
среднеквадратическое отклонение
погрешности (СКО) (корень квадратный из
дисперсии); доверительный интервал,
задаваемый верхней
и нижней
границами и доверительная вероятность
,
связанные соотношением
,
где P{
}–вероятность выполнения неравенства
в { }.
При
=1
и симметричном относительно нулевого
значения доверительном интервале
в качестве характеристики погрешности
используется граничные (предельные)
значения погрешности равные 
.