12. Сравнения и вычеты. Кольцо вычетов. Малая терема Ферма. Сравнения первой степени. Китайская теорема об остатках.

Сравнения

Зафиксируем натуральное число т => 1, которое условимся называть модулем.

Определение 1. Два целых числа а, b назовем сравнимыми по модулю т, если они при делении на т дают одинаковые остат­ки. Обозначение:

Рассмотрим простейшие свойства сравнений.

Сравнения первой степени – с-ва

Теорема 1. Сравнения целых чисел по модулю т обладают следующими свойствами для любых а, b, с, d € Z:

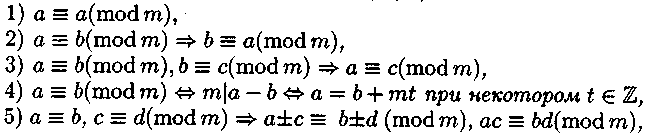
(т. е. сравнения можно почленно складывать, вычитать и перемножать),

6) если d есть общий делитель чисел а, b, т, то

7) если числа а, b делятся на d и d взаимно просто с т, то

Классы вычетов по модулю т

Из свойств 1) — 3) сравнений видно, что отношение сравнимо­сти целых чисел по модулю т является отношением эквивалент­ности, и, следовательно, множество целых чисел разбивается на непересекающиеся классы сравнимых по модулю m чисел. Так как различные остатки при делении на т исчерпываются числами 0,1,2,...,m-1, то получим т классов: (2) где через обозначен класс всех чисел, которые при делении на т дают в остатке r. Очевидно, что класс однозначно определяется любым одним своим представителем, и потому в даль­нейшем класс будет обозначаться также в виде , где а — любой представитель этого класса.

Классы (2) называются классами вычетов, а их элементы — вычетами по модулю т. Из определения сравнений следует, что числа из одного класса сравнимы по модулю т, а числа из разных классов не сравнимы по модулю т, т. е.

Определение 1. Совокупность чисел, взятых по одному из каждого класса вычетов по модулю т, называется полной систе­мой вычетов по модулю т.

Примером полной системы вычетов по модулю т является множество чисел 0,1,... , m — 1. Это так называемая полная система наименъшцх неотрица­тельных вычетов.

Cледующее свойство полных систем вычетов.

Теорема 1. Если есть полная система вычетов по модулю т, число а взаимно простое с т и b — любое целое число, то (3) есть также полная система вычетов по модулю т.

Доказательство (можно не писать – М.С.). Все числа ряда (3) принадлежат разным классам вычетов по модулю т, поскольку в силу свойств сравнений А так как в (3) содержится т чисел, т. е. столько же чисел, сколь­ко и классов, то в (3) имеется ровно по одному представителю из каждого класса. Следовательно, (3) есть полная система вычетов по модулю т

Малая терема Ферма

Теорема. Если натуральные числа а, т взаимно просты, то

Следствие. Если р — простое число и , то

Для доказательства утверждения а) достаточно заметить, что . Утверждение б) при следует из а) и следствия 1 теоремы 2, а при очевидно, поскольку в этом случае

.

Заметим, что утверждение а) следствия впервые доказал Ферма, оно называется малой теоремой Ферма. Теорема б была позднее доказана Эйлером и носит название теоремы Эйлера — Ферма. Она находит ши­рокое применение в математике и ее приложениях и, в частности, может оказаться полезной при нахождении остатков от деления степеней чис­ла на заданное число, при решении сравнений с неизвестными и т. д.

Кольцо вычетов

Рассмотрим множество всех классов вычетов по модулю . Класс состоит из всех чисел вида , где t пробегает множество Z, т. е.

Следовательно, классы вычетов по модулю та совпадают со смеж­ными классами кольца Z по его идеалу mZ.

Теорема 1. Определение операций сложения и умножения классов вычетов по формулам

корректно, и множество с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо кольца Z по его идеалу тZ.

Кольцо Z/rn называют кольцом классов вычетов по модулю т.

Опишем обратимые элементы этого кольца.

Теорема 2. Элемент обратим в кольце Z/m тогда и только тогда, когда класс взаимно прост с т, т. е. (а,т) = 1.

Китайская теорема об остатках

Пусть m - натуральное число, m₁, m₂, ..., m_t - взаимно простые натуральные числа, произведение которых больше либо равно m.

Теорема:

Любое число x: 0 <= x <= m может быть однозначно представлено в виде последовательности r(x) = (r1, r2, ..., rt), где ri = x(mod mi).

Для любых чисел r1 .. rt, таким образом, существует единственное число x(mod m), такое что

x = ri(mod mi), 1 <= i <= t

Более того, любое решение x набора такого сравнений имеет вид

x = r1*e1 + ... + rt*et (mod m), где ei = m / mi * ( ( m/mi )-1 mod mi ), 1 <= i <= t.

14. Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе.

Обход в глубину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода):

1) Рассматриваем вершину Х. Двигаемся в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину;

2) Если из вершины Х нельзя попасть в ранее непосещенную вершину или таковой нет, то возвращаемся в вершину Z, из которой впервые попали в X, и продолжаем обход в глубину из вершины Z.

3) Такой обход графа продолжается до тех пор, пока очередная вершина Х, не совпадет с вершиной Х₀,с которой начался обход графа (компоненты связности).

Обход в ширину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода):

1) Рассматриваем вершину Х. Ей присваивается метка 0;

2) Всем смежным вершинам с вершиной с меткой 0 поочередно присваиваются метки 1;

3) Всем смежным вершинам с вершинами с меткой 1 поочередно присваиваются метки 2;

4) И т.д. до тех пор, пока не будут помечены все вершины в текущем графе (компоненте связности).

Связный граф

Граф, в котором все вершины связаны.

Остовное дерево связного графа

Любой его подграф, содержащий все вершины графа G и являющийся деревом (т.е. не содержит циклов и из одной вершины в другую можно попасть единственным путем). Определяется неоднозначно.

Компонента связности графа

Некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Лес

Неориентированный граф без циклов (может быть и несвязным). Компонентами связности леса являются деревья (т.е. лес это тот же неориентированный граф, который может быть несвязным).

Сильно связный ориентированный граф (или сильный)

Орграф называется сильно связным или сильным, если для любых двух различных вершин x_i и x_j существует, по крайней мере, один путь, соединяющий x_i с x_j, т.е. любые две вершины такого графа взаимно достижимы (т.е. из каждой можно попасть в каждую).

Односторонне связный ориентированный граф

Орграф называется односторонне связным, если для любых двух различных вершин x_i и x_j существует, по крайней мере, один путь из x_i в x_j или из x_j в x_i. (т.е. можно попасть либо из x_i в x_j либо из x_j в x_i)

Слабо связный ориентированный граф (или слабый)

Орграф называется слабо связным, если для любых двух различных вершин x_i и x_j существует, по крайней мере, один маршрут соединяющий их (т.е. например из x_i можно попасть в любую x_j, но в саму x_i нельзя попасть ни из какой другой вершины).

Несвязный ориентированный граф

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой граф называется несвязным.

Компонента сильной связности в орграфе

Сильно связными компонентами орграфа называются его максимальные по включению сильно связные подграфы.

Алгоритм построения глубинного остовного леса:

Шаг 1. Выбираем в G произвольную вершину u₁, которая образует подграф G_i леса G, являющийся деревом.

Шаг 2. Если i = n, где n = n(G) (проверка на наличие всех вершин исходного леса в построенном остовном лесу), то задача решена, и G_i, искомый остовный лес леса G. В противном случае переходим к шагу 3.

Шаг 3. Пусть уже построено дерево G_i, являющееся подграфом леса G и содержащее некоторые вершины u₁, ...u_i, где 1 < i < n-1. Строим граф G_i+1, добавляя к дереву G_i новую вершину u_i+1, смежную в G с некоторой вершиной u_j графа G_i, и новое ребро {u_i+1 , u_j}.Если такое ребро есть, то присваиваем i := i + l и переходим к шагу 2. Если невозможно найти ребро, соединяющее вершину u_i+1 с вершиной u_j (в силу возможной несвязности леса G), то переходим к шагу 4.

Шаг 4. Принимаем вершину u_j+1 из шага 3 за начало нового дерева в лесу G, присваиваем i := i + l и переходим к шагу 2.

К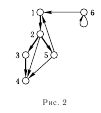 лассификация ребер оргафа

1. Ребра деревьев — это ребра, входящие в лес поиска в глубину. На рис. 2 это ребра (1, 2), (2, 3), (2, 5), (3, 4).

2. Обратные ребра — это ребра, соединяющие вершину с ее предком в дереве поиска в глубину (ребра-циклы, возможные в ориентированных графах, считаются обратными ребрами). На рис. 2 это ребра (5, 1), (6, 6).

3. Прямые ребра — это ребра, соединяющие вершину с ее потомком, но не входящие в лес поиска в глубину: (2, 4) на рис. 2.

4. Перекрестные ребра—все остальные ребра графа. Они могут соединять две вершины из одного дерева поиска в глубину, если ни одна их этих вершин не является предком другой, или же вершины из разных деревьев: (5, 4), (6, 1) на рис. 2.

Выделение компонент связности в неориентированном графе

Этап 1(первоначальная разметка):

Шаг 1.Пометить все вершины графа маркером «1»;

Шаг 2. Пометить любую вершину с маркером «1» маркером «2»;

Этап 2 (разметка соседних вершин):

Шаг 3. Если нет вершин, помеченных маркером «2» - переходим к этапу 3;

Шаг 4. Выбираем любую вершину с маркером «2», помечаем ее маркером «3», а все соседние вершины, помеченные маркером «1», помечаем маркером «2». Затем повторяем этот этап сначала;

Этап 3 (сбор результатов):

Шаг 5. Если нужно получить список вершин, входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные третьим маркером;

Шаг 6. Если нужно получить список вершин, не входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные маркером «1»;

Шаг 7. Если нужно просто проверить граф на связность, то считаем вершины, помеченные первым маркером, и сравниваем получившееся число с нулем. Если число вершин, помеченных первым маркером, равно нулю, то граф связный.

Выделение компонент сильной связности в орграфе

Этап 1(первоначальная разметка):

Шаг 1.Пометить все вершины графа маркером «1»;

Шаг 2. Пометить любую вершину с маркером «1» маркером «2»;

Этап 2 (разметка соседних вершин):

Шаг 3. Если нет вершин, помеченных маркером «2» и все вершины в графе помечены маркером «D_i» - переходим к этапу 3. Если нет вершин, помеченных маркером «2», но есть вершины с маркером «1» и без маркера «D_i», то i = i + 1 и переходим к шагу 2. Если есть вершина с маркером «2», переходим к шагу 4;

Шаг 4. Выбираем любую вершину v с маркером «2», помечаем ее маркером «3» и маркером «D_i» (если она еще не помечена маркером «D_i») (здесь i - номер компоненты связности), а все соседние вершины u, достижимые из этой вершины и помеченные маркером «1», помечаем маркером «2». Если нет достижимых соседних вершин с маркером «1», то повторяем этап 2.

Шаг 5. Проверяем, есть ли путь из вершины u обратно в вершину v. Если есть – помечаем вершину u маркерами «3» и «D_i». Если нет – снова помечаем вершину u маркером «1». Затем повторяем этот этап сначала;

Этап 3 (сбор результатов):

Шаг 6. Если нужно получить список вершин, входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные соответствующим маркером «D_i»;

Шаг 7. Если нужно получить список вершин, не входящих в компоненту связности «D_i» то выбираем вершины, помеченные маркером, отличным от маркера «D_i»;

Таким образом, результатом данного алгоритма будут:

1. количество компонент сильной связности;

2. сгруппированные по компонентам связности вершины орграфа;

Поиск в ширину и кратчайшие пути в графе

Поиск в ширину находит расстояния до каждой достижимой вершины в графе от исходной вершины s. Определим длину кратчайшего пути δ(s,v) как минимальное количество ребер на пути от s к v, если пути не существует, то δ(s,v) = ∞. CСледующий алгоритм вычисляет длины кратчайших путей.

1. Пусть G=(V,E) – ориентированный или неориентированный граф, а s – его произвольная вершина, тогда для любого ребра (u,v) графа справедливо δ(s,v) ≤ δ(s,u)+1.

2. Пусть в данном графе процедура поиска (//обхода) в ширину выполняется с исходной вершиной s. Тогда по завершении процедуры для каждой вершины графа v справедливо d[v] ≥ δ(s,v). Где d[v] – метка времени, показывающая, на каком шаге алгоритма обхода в ширину была достигнута вершина v. По сути – расстояние от v до s.

3. Следствием выполнения процедуры поиска в ширину над графом G=(V,E) является монотонное увеличение параметра d, при каждом следующем шаге алгоритма обхода в ширину.

4. Таким образом, в процессе своей работы алгоритм обхода в ширину открывает все вершины v ∈ V, достижимые из s, и по окончании работы алгоритма для каждой v_i∈V будет справедливо d[v_i]= δ(s,v). Кроме того, для всех достижимых из s вершин v ≠ s, один из кратчайших путей от s к v – это путь от s к π[v], за которым следует ребро (π[v], v), где π[v] – вершина, из которой мы попали в вершину v, в процессе процедуры поиска в ширину.

13. Системы линейного уравнения над кольцом и полем. Системы линейных уравнений над коммутативным кольцом с единицей. Равносильность систем. Системы уравнений над кольцом. Однородные уравнения и функциональная система решений.

Введём понятие кольца и поля

Кольцо — это множество М с двумя бинарными операциями в котором:

1. сложение ассоциативно;

2. существует нуль;

3. существует обратный элемент;

4. сложение коммутативно

5. умножение ассоциативно

6.

Кольцо называется коммутативным, если

7. умножение коммутативно.

Коммутативное кольцо называется кольцом с единицей, если

8. существует единица

Поле — это множество М с двумя бинарными операциями такими что:

1. сложение ассоциативно;

2. существует нуль;

3. существует обратный элемент по сложению;

4. сложение коммутативно

5. умножение ассоциативно;

6. существует единица;

7. существует обратный элемент по умножению;

8. умножение коммутативно

9. умножение дистрибутивно относительно сложения.

Определим понятие системы линейных уравнений

В общем случае система линейных уравнений с неизвестными (или, кратко, линейная система) имеет следующий вид:

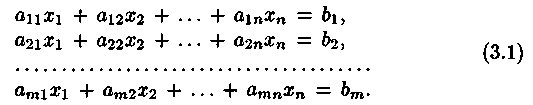
При этом через обозначены неизвестные, подлежащие определению (число их n не предполагается обязательно равным числу уравнений m); величины называемые коэффициентами системы, и величины называемые свободными членами, предполагаются известными.

Система (3.1) называется однородной, если все ее свободные члены равны нулю.

Если хотя бы один из свободных членов отличен от нуля, то система (3.1) называется неоднородной.

Система (3.1) называется квадратной, если число т составляющих ее уравнений равно числу неизвестных п.

Решением системы (3.1) называется такая совокупность чисел которая при подстановке в систему (3.1) на место неиз­вестных обращает все уравнения этой системы в тожде­ства.

Система уравнений вида (3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения.

Совместная система вида (3.1) может иметь или одно решение, или несколько решений.

Два решения совместной системы вида и

называются различными, если нарушается хотя бы одно из равенств

Совместная система вида (3.1) называется определенной, если она имеет единственное решение.

Совместная система вида (3.1) называется неопределенной, если у нее существуют по крайней мере два различных решения.

Для произвольного основного поля Р остаются справедливыми метод Гаусса для решения систем линейных уравнений, теория определителей и правило Крамера.

Полностью переносятся на случай произвольного основного поля теория линейной зависимости векторов, теория ранга матрицы и общая теория систем линейных уравнений, а также алгебра матриц.

Теорема Кронекера-Капелли: система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы В равен рангу матрицы А.

Рассмотрим всевозможные упорядоченные конечные системы элементов поля Р, имеющие вид: (а₀, а₁, …, а_n-1, а_n) (1), причем n произвольно, n≥0, но при n>0 должно быть a_n≠0. Определяя для систем вида (1) сложение и умножение в соответствии с формулами:

Если даны многочлены f(x) и g(x) с комплексными коэффициен­тами, записанные для удобства по возрастающим степеням х:

f(x)=a₀ + a₁x + … + a_n-1x^n-1 + a_nxⁿ, a_n≠0

g(x)=b₀ + b₁x + …+ b_s-1x^s-1 + b_sx^s, b_s≠0

и если, например, n>=s, то их суммой называется многочлен

f(x)+g(x)=c₀+c₁x+…+c_s-1x^s-1+c_sx^s , где c_i=a_i+b_i, i=0,1, …,n.

причем при n>s коэффициенты b_s+1 b_s+2, ..., b_п следует считать равными нулю. Степень суммы будет равна n, если n больше s, но при n=s она может случайно оказаться меньше n, а именно в слу­чае b„== - а_п.

Произведением многочленов f{x) и g{x) называется многочлен

f(x)*g(x)=d₀+d₁x+…+d_n+s-1x^n+s-1+d_n+sx^n+s , где d_i= , i=0,1, …, n+s.

т. е. коэффициент d_t есть результат перемножения таких коэффи­циентов многочленов /(х) и g(x), сумма индексов которых равна i, и сложения всех таких произведений; поэтому степень произведения двух много­членов равна сумме степеней этих многочленов.

Отсюда следует, что произведение многочленов, отличных от нуля, никогда не будет равным нулю.

Какими свойствами обладают введенные нами операции для много­членов? Коммутативность и ассоциативность сложе­ния немедленно вытекают из справедливости этих свойств для сло­жения чисел, так как складываются коэффициенты при каждой степени неизвестного отдельно. Вычитание оказывается выполнимым: роль нуля играет число нуль, включенное нами в число много­членов, а противоположным для записанного выше много­члена f(х) будет многочлен

-f(x) = — а₀—а₁х— ... —a_n-1x^n-1—a_nxⁿ

Коммутативность умножения вытекает из коммутатив­ности умножения чисел и того факта, что в определении произведения многочленов коэффициенты обоих множителей f(x) и g(x) исполь­зуются совершенно равноправным образом. Ассоциативность умножения доказывается следующим образом: если, помимо запи­санных выше многочленов f(х) и g{x), дан еще многочлен

h(x)=c₀ + c₁x + …+ c_t-1x^t-1 + c_tx^t, c_t≠0

то коэффициентом при хⁱ, i = 0, 1, ..., n+s+t в произведении [f(x)g(x)]h(x) будет служить число

в произведении f(x)[g(x)h(x)] — равное ему число

Наконец, справедливость закона дистрибутивности вытекает из равенства

так как левая часть этого равенства является коэффициентом при Xⁱ в многочлене [f(x)+g(x)]h(x), а правая часть —коэффициентом при той же степени неизвестного в многочлене f(x)h{x) + g(x)h(x). Заметим, что роль единицы при умножении многочленов играет число 1, рассматриваемое как многочлен нулевой степени. С другой стороны, многочлен f(x) тогда и только тогда обладает обрат­ным многочленом f^-1(х), f(x) f^-1(х) = 1, если f{x) является многочленом нулевой степени. Действительно, если f(x) является отличным от нуля числом а, то обратным много­членом служит для него число а^-1. Если же f(x) имеет степень n>=1, то степень левой части равенства f(x) f^-1(х) = 1, если бы многочлен f^-1(х) существовал, была бы не меньше n, в то время как справа стоит многочлен нулевой степени.

Правило решения произвольной системы линейных уравнений: пусть дана совместная система линейных уравнений 3.1 и пусть матрица из коэффициентов А имеет ранг r. Выбираем в А r линейно независимых строк и оставляем в системе 3.1 лишь уравнения, коэффициенты которых вошли в выбранные строки. В этих уравнениях оставляем в левых частях такие r неизвестных, что определитель при коэффициентах при них отличен от нуля, а остальные неизвестные объявляем свободными и переносим в правые части уравнений. Давая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных по правилу Крамера, мы получим все решения системы.

Докажем что квадратная система линей­ных уравнений (3.10) с определителем основной матрицы, отличным от нуля, имеет, и притом единственное, решение, определяемое фор­мулами Крамера (1)

В случае, когда дана системы линейного уравнения над кольцом с определителем основной матрицы, отличным от нуля кольца, эта система имеет и притом единственное, решение, определяемое фор­мулами Крамера

Теорема. Квадратная матрица М над кольцом об­ратима тогда и только тогда, когда то есть определитель взаимно прост с

Доказательство (1)

Пусть дана квадрат­ная система линейных уравнений

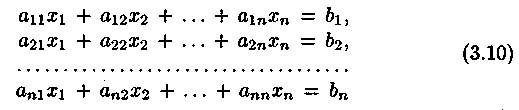
с отличным от нуля определителем основной матрицы

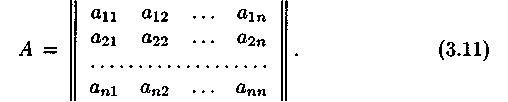
Докажем, что система (3.10) может иметь только одно решение (т. е. докажем единственность решения си­стемы (3.10) в предположении его существования).

Предположим, что существуют какие-либо п чисел такие, что при подстановке этих чисел в систему (3.10) все уравне­ния этой системы обращаются в тождества. Тогда, умножая тождества (3.10) соответственно на алгебраические дополнения элементов столбца определителя матрицы (3.11) и складывая затем получающиеся при этом тождества, мы получим (для любого номера равного

Учитывая, что сумма произведений элементов го столбца на соответ­ствующие алгебраические дополнения элементов столбца равна нулю при и равна определителю матрицы (3.11) при мы получим из последнего равенства

Обозначим символом (или, более кратко, символом ) определитель, получающийся из определителя основной матри­цы (3.11) заменой его столбца столбцом из свободных членов (с сохранением без изменения всех остальных столб­цов

Заметим, что в правой части (3.12) стоит именно определитель ⁹), и это равенство принимает вид

Поскольку определитель матрицы (3.11) отличен от нуля, равен­ства (3.13) эквивалентны соотношениям

Итак, мы доказали, что если решение системы (3.10)

с определителем основной матрицы (3.11), отличным от ну­ля, существует, то это решение однозначно определяется форму­лами (3.14).

Формулы (3.14) называются формулами Крамера ¹⁰).

Еще раз подчеркнем, что формулы Крамера пока получены нами в предположении существования решения и доказывают его единствен­ность.

Остается доказать существование решения системы (3.10). Для это­го в силу теоремы Кронекера-Капелли достаточно доказать, что ранг основной матрицы (3.11) равен рангу расширенной матрицы ^п)

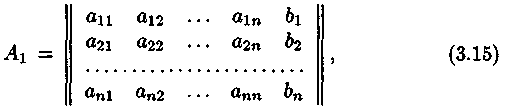
но это очевидно, ибо в силу соотношения ранг основной матрицы равен а ранг содержащей п строк расширенной матрицы (3.15) больше числа п быть не может и потому равен рангу основной матрицы. Тем самым полностью доказано.

Равносильность. Два многочлена f(x) и g(x) будут считаться равными (или тождественно равными), f(x)=g(x), если равны их коэффицменты при одинаковых степенях неизвестного.

Пусть матрица А из коэффициентов системы однородных ЛУ имеет ранг r. Если r=n, то нулевое решение будет единственным решением однородной СЛУ. При r<n система обладает также решениями, отличными от нулевого, и для разыскания всех этих решений применяется тот же прием, как выше в случае произвольной системы уравнений. В частности, система n линейных однородных уравнений с n неизвестными тогда и только тогда обладает решениями, отличными от нулевого, если определитель этой исстемы равен нулю. Если в системе однородных уравнений число уравнений меньше числа неизвестных, то система непременно обладает решениями, отличными от нулевого, т.к. ранг в данном случае не может быть равным числу неизвестных.

Поэтому вообще всякая линейная комбинация решений однородной системы будет сама решением этой системы. Но в случае неоднородной системы, т.е. системы линейных уравнений, свободные члены которых (правые части) не все равны 0, соответствующее утверждение не имеет места: ни сумма двух решений системы неоднородных уравнений, ни произведение решения этой системы на число не будут решениями для этой системы.

Известно, что всякая система n-мерных векторов, состоящая более чем из n векторов, будет линейно зависимой. Отсюда следует, что из числа решений однородной системы, являющихся n-мерными векторами, можно выбрать конечную максимальную линейно независимую систему, максимальное в том смысле, что всякое другое решение однородной СЛУ будет линейной комбинацией решений, входящих в эту выбранную систему. Всякая максимальная линейно независимая система решений однородной СЛУ называется ее фундаментальной системой решений. Фундаментальная система решений будет существовать лишь в том случае, если система однородных ЛУ обладает ненулевыми решениями, т.е. если ранг ее матрицы из коэффициентов меньше числа неизвестных. При этом система однородных ЛУ может обладать многими различными фундаментальными системами решений. Все эти системы эквивалентны между собой, т.к. каждый вектор всякой из этих систем линейно выражается через любую другую систему, поэтому системы состоят из одного и того же числа решений.

Теорема: если ранг r матрицы из коэффициентов системы линейных однородных уравнений меньше числа неизвестных n, то всякая фундаментальная система решений этой СЛУ состоит из n-r решений.

14. Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе.

Обход графа в глубину – метод систематического прохождения (посещения) вершин графа, когда за счет продвижений от текущей вершины по ребру вперед (к еще непросмотренной вершине) всегда, когда это возможно, и возвратов от текущей вершины по пройденному ребру назад (к ранее пройденной вершине), если движение вперед от текущей вершины невозможно, осуществляется движение по всем вершинам графа, достижимым из заданной вершины s, с которой начинается поиск. Поиск в глубину всегда завершается через конечное число шагов в вершине s - начале просмотра.

Осуществляется по следующим правилам:

(1) находясь в вершине x, нужно двигаться в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину; (2) если из вершины x мы не можем попасть в ранее непосещенную вершину или таковой нет, то мы возвращаемся в вершину z, из которой впервые попали в x, и продолжаем обход в глубину из вершины z. При выполнении обхода графа по этим правилам мы стремимся проникнуть "вглубь" графа так далеко, как это возможно, затем отступаем на шаг назад и снова стремимся пройти вперед и так далее. Таким образом, допустим, что мы находимся в вершине графа v. Далее, выбираем произвольную, но еще не просмотренную вершину u, смежную с вершиной v. Эту новую вершину рассматриваем теперь уже как v и, начиная с нее, продолжаем обход. Если не существует ни одной новой (еще не просмотренной) вершины, смежной с v, то говорят, что вершина v просмотрена и возвращаются в вершину, из которой мы попали в v. Поиск продолжается до тех пор, пока v=v_0.

Остовное дерево связного графа

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом

Пусть G — связный граф. Тогда в силу утверждения 4.35 остовное дерево графа G (если оно существует) должно содержать n(G) — 1 ребер. Таким образом, любое остовное дерево граф! есть результат удаления из G ровно m(G) — (n(G) -= m(G) — n{G) + 1 ребер.

Число m(G)—n(G) + 1 называется цикломатическим числом связного графа G и обозначается через v(G).

Покажем существование остовного дерева для произвольного связного псевдографа G = (V, X), описав алгоритм его выделения.

Алгоритм 4.6:

Шаг 1. Выбираем в G произвольную вершину иг, которая _ разует подграф Gi псевдографа G, являющийся деревом. Пол гаем t= 1.

Шаг 2. Если i = п, где п = n(G), то задача решена, и G, искомое остовное дерево псевдографа G. В противном случае п реходим к шагу 3.

Шаг 3. Пусть уже построено дерево Gi, являющееся подграфом псевдографа G и содержащее некоторые вершины u₁, ...u_i, где 1<i<n-1. Строим граф G_i+i, добавляя к графу G_; новую вершину Ui+iЭV, смежную в G с некоторой вершиной u_j графа G_i,-, и новое ребро {u_i+1 , u_j} (в силу связности G и того обстоятельства, что i<n, указанная вершина u_i+1 обязательно найдется). Согласно утверждению 4.36 граф G_i+1 также является деревом. Присваиваем i: =i+l и переходим к шагу 2.

Выделение компонент связности

Опишем алгоритм нахождения числа компонент сильной связ­ности орграфа, а также выделения этих компонент. Аналогич­ным образом решается задача нахождения количества компо­нент связности, а также выделения компонент связности неори­ентированного графа. Однако для определенности приводим рассуждения для орграфа.

Воспользуемся следующими утверждениями.

Утверждение 4.18. Пусть D — орграф с р≥2 компонентами сильной связности: D₁ ...,D_P. Тогда в результате удаления из D вершин, содержащихся в D₁ получаем орграф с р—1 компонен­тами сильной связности: D₂ ..., D_p.

-Воспользуемся тем очевидным фактом, что если D' — компо­нента сильной связности орграфа D, то D' является компонен­той сильной связности и любого подграфа орграфа D, содержа­щего все вершины и дуги орграфа D'. Используя утверждение 4.11, п. 2, заключаем, что после удаления из D вершин, содержащихся в D₁, имеем орграф D, подграфами которого являются D₂, ..., Dp, а следовательно, D₂, ..., D_p являются компонентам^ сильной связности орграфа D. Кроме того, в силу утверждения 4.11, пп. 1, 2, получаем, что объединение множеств вершин ор­графов D₂, ..., Dp дает множество вершин орграфа D, а значит, D₂, ..., Dp — все компоненты сильной связности орграфа D.

Утверждение 4.11. Пусть D = (V, X)—ориентированный псевдограф с р компонентами сильной связности: D₁ = (V₁ ,Х₁), ..., D_P = (V_P, X_p). Тогда

1. V=ViU..UV,, X=>X₁U...UX_p;

2. V_iЛV_j =Ø, X_iЛX_j=Ø при i≠j,

3. n(n_i)+...+n(D_p)=n(D),m(D_l)+...+m(D_p)≤ m(D).

Утверждение 4.19. Пусть D' — компонента сильной связнос­ти орграфа D. Пусть также p(D)≥2 и D" — орграф, получаемый в результате удаления из D вершин, содержащихся в D', Тогда матрицами A(D"), S(D") являются подматрицы матриц A(D), S(D), получаемые в результате удаления из них строк и столбцов, соответствующих вершинам орграфа D'.

Утверждение 4.19 является следствием утверждений 4.18 и 4.14.

Из определения матрицы сильной связности вытекает, что справедливо

Утверждение 4.20. Единицы i-й строки или i-го столбца матрицы сильной связности орграфа D = (V, X), где V={v_x, ..., v_n), соответствуют вершинам компоненты сильной связности ор­графа D, содержащей вершину v_i.

Из утверждений 4.18—4.20 следует справедливость алгорит­ма определения числа компонент сильной связности орграфа D, а также матриц смежности этих компонент.

Алгоритм 4.1:

Шаг 1. Полагаем р = 1, Si=S(D).

Шаг 2. Включаем в множество вершин V_p очередной компо­ненты сильной связности Dp орграфа D вершины, соответствую­щие единицам первой строки матрицы S_p. В качестве A (D_p) бе­рем подматрицу матрицы A(D), находящуюся на пересечении строк и столбцов, соответствующих вершинам из V_p.

Шаг 3. Вычеркиваем из S_p строки и столбцы, соответствую­щие вершинам из V_p. Если в результате такого вычеркивания не остается ни одной строки (и соответственно ни одного столб­ца), то р —количество компонент сильной связности и A (Di), ... ..., A (Dp) — матрицы смежности компонент сильной связности Di, ..., Dp орграфа D. В противном случае обозначаем оставшу­юся после вычеркивания из S_p соответствующих строк и столб­цов матрицу через S_p+1, присваиваем р : =р+1 и переходим к шагу 2.