10. Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема Безу.

Пусть - непустое множество, на котором заданы две бинарные операции: сложение и умножение, удовлетворяющие следующим условиям:

1) Структура есть абелева группа, то есть сложение коммутативно и ассоциативно, существует нейтральный элемент (ноль) по сложению и для любого существует единственный противоположный к нему элемент.

2) Структура есть полугруппа, то есть умножение ассоциативно;

3) Операции сложения и умножения связаны законом дистрибутивности: Структура и для любых .

Тогда алгебраическая структура называется кольцом.

Пусть - произвольное кольцо с единицей . Многочленом над назовем любую бесконечную последовательность элементов , в которой все , за исключением конечного их числа, равны нулю. Элементы назовем коэффициентами многочлена. Многочлен назовем нулевым. Обозначим через множество всех таких последовательностей. Номер последнего ненулевого члена последовательности назовем степенью многочлена и обозначим .

Суммой многочленов называют последовательность , в которой для всех .

Произведением многочленов называют последовательность , в которой для всех .

Произведением многочлена на элемент слева или справа называют, соответственно, последовательность или .

Суммой элемента и многочлена называют последовательность .

Во всех последовательностях в вышеприведенных определениях, так же как и в исходных последовательностях, все коэффициенты, за исключением конечного их числа, равны нулю, и потому эти последовательности принадлежат .

Используя заданные на операции, можно перейти к традиционной форме записи многочленов. Введем обозначени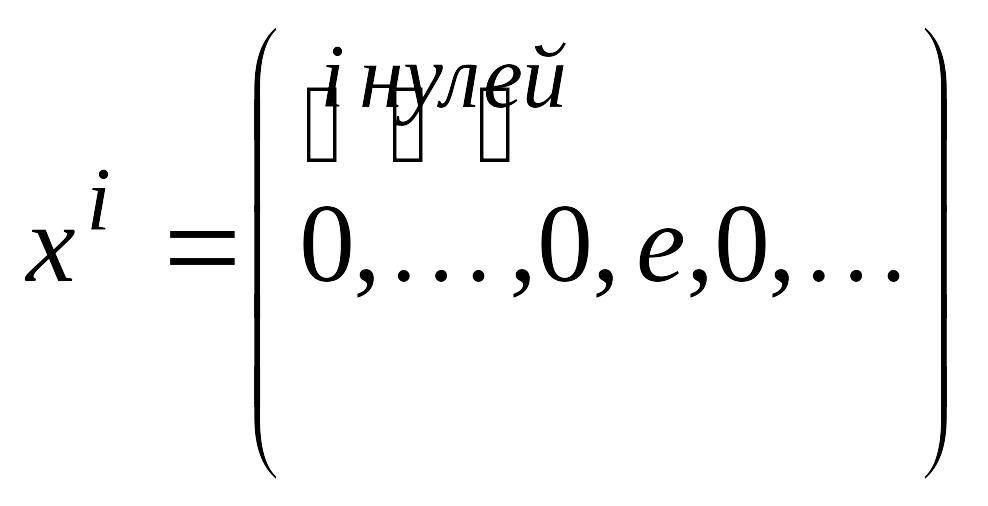я: , для .

Заметим, что ввиду определения произведения многочленов для любых выполняются равенства:

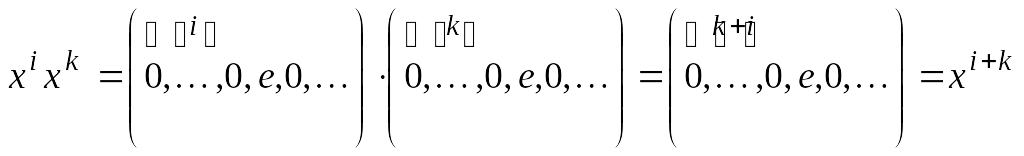
Поэтому для любых верны равенства и для символ обозначает ни что иное, как -ю степень элемента : .

Пользуясь определением произведения многочлена на элемент множества , получаем, что для любых и верны равенства , и поэтому любой многочлен может быть записан в виде суммы:

Последнюю запись многочлена можно еще упростить, записав его в общепринятом виде: .

При введенных обозначениях многочлен называют многочленом от над кольцом , а элементы называют его коэффициентами. Говорят, что - коэффициент многочлена при , а - его свободный член. Множество называют множеством многочленов от одного переменного над кольцом и обозначают: .

Алгебра многочленов над кольцом с единицей есть кольцо с единицей. Кольцо коммутативно тогда и только тогда, когда кольцо коммутативно, и содержит делители нуля тогда и только тогда, когда содержит делители нуля.

Говорят, что элемент кольца делится на элемент слева (справа), если в разрешимо уравнение .

Однако если - кольцо многочленов над кольцом с единицей, то в можно ввести понятие делимости с остатком и предложить алгоритм, который позволяет проверить, делится один многочлен на другой или нет.

Говорят, что в кольце многочлен делится на многочлен справа с остатком, если существуют многочлены со свойствами , . //(deg – обозначение степени многочлена)

При этом многочлены и называют, соответственно, неполным правым частным и правым остатком от деления на . Аналогично определяется понятие делимости на слева с остатком.

Если старший коэффициент многочлена обратим в кольце , то любой многочлен можно разделить справа (слева) с остатком на . При этом правые (левые) неполное частное и остаток определяются однозначно.

Если - поле и , то любой многочлен можно разделить с остатком на и притом единственным способом.

Значением многочлена из в точке называют элемент кольца . Говорят, что - корень многочлена , если .

Данное определение позволяет поставить в соответствие каждому многочлену функцию , определяемую условием .

Очевидно, что значение суммы двух многочленов в любой точке равно сумме их значений. Для произведения многочленов аналогичное утверждение верно не всегда.

Если , и элемент перестановочен со всеми коэффициентами правого множителя , то . При сформулированном условии верны равенства .

Теорема Безу. Остаток от деления справа многочлена на двучлен равен . В частности, элемент

кольца является корнем многочлена тогда и только тогда, когда делится справа на .

Доказательство. //(хз надо или нет) можно разделить справа с остатком на : , . Тогда , где , и . Так как для многочлена верно равенство , то . В частности, равенство эквивалентно равенству , а последнее эквивалентно тому, что делит справа .

11. Кольца матриц. Матрицы над кольцом и операции над ними. Кольцо квадратных матриц. Определители квадратных матриц над коммутативным кольцом с единицей. Критерий обратимости матрицы над коммутативным кольцом с единицей.

Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов.

Числа m, n наз. порядком матрицы. Если m=n, матрица называется квадратной.

Множество квадратных матриц порядка n относительно операции сложения и умножения матриц есть кольцо с единицей Е – единичной матрицей, при n>1 оно некоммутативно.

Операции над матрицами:

С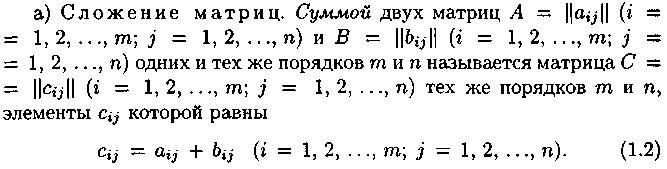 ложение матриц обладает переместительным свойством: А + В = Б + А; и сочетательным свойством: (А + В) + С = А + (В + С).

Д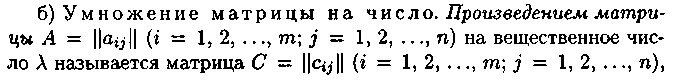 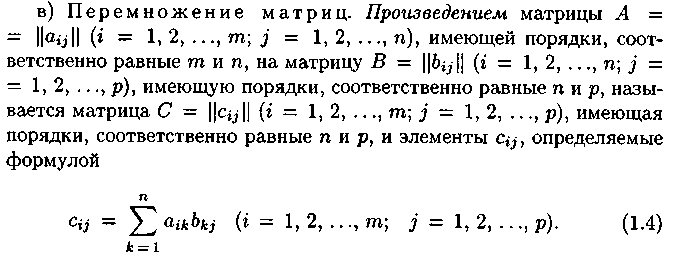ля обозначения произведения матрицы на число используется за­пись или . Операция составления произведения мат­рицы на число называется умножением матрицы на это число. Умножение матрицы на число обладает 1)сочетательным свойством относительно числового множителя: 2)распределительным свойством относительно суммы матриц: 3)распределительным свойством относительно суммы чисел:

Матри­цу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было = числу строк матрицы В. Для того чтобы оба произведения А *B и B*A были определены необходимо и достаточно, чтобы обе матрицы A и В были квадр матрицами одного и того же порядка.

Определители

Кольцо коммутативно если а*b=b*a – умножение коммутативно

Коммутативное Кольцо с единицей если существует 1ЄМ а*1=1*а=а

Если порядок матрицы равен единице, то эта матрица состоит из одного элемента и определителем первого порядка, со­ответствующим такой матрице, мы назовем величину этого элемента. Если далее порядок матрицы равен двум, то определителем второго порядка, соответствующим такой матрице, назовем число, равное и обозначаемое одним из символов . Итак, по определению (1.10) Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы.

Перейдем теперь к выяснению понятия определителя любого по­рядка п , где Понятие такого определителя мы введем индуктив­но, считая, что нами уже введено понятие определителя порядка п — 1, соответствующего произвольной квадратной матрице порядка п — 1.

Договоримся называть минором любого элемента матрицы n-го порядка (1.8) определитель порядка п — 1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i-й строки и j-го столбца (той строки и того столбца, на пересечении которых стоит элемент ). Минор элемента будем обозначать символом . В этом обозначении верхний индекс обозна­чает номер строки, нижний — номер столбца, а черта над М означает, что указанные строка и столбец вычеркиваются.

Определителем порядка п, , на­зовем число, равное

Итак, по определению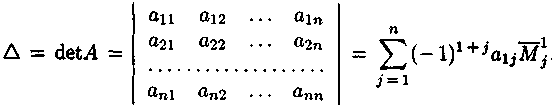 . (1.12)

Формула (1.12) представляет собой правило составления определителя порядка п по элементам первой строки соответствующей ему матрицы и по минорам элементов первой строки, являющимися определителями порядка п — 1.

К – кольцо с единицей. Элемент а называется обратимым, if существует такой элемент а^-1, для которого аа^-1=а^-1а=1.

Понятие обратной матрицы. Пусть А —квадратная матрица n-го порядка, а Е — единичная квадратная матрица того же порядка Матрица В называется правой обратной по отношению к матри­це А, если АВ = Е. Матрица С называется левой обратной по отношению к матрице А, если С А = Е.

Теорема. Для того, чтобы для матрицы А существовали левая и правая обратные матрицы, необходимо и достаточно, чтобы определитель det А матрицы А был отличен от нуля.

Замечание 1. Квадратную матрицу А, определитель det А которой отличен от нуля, принято называть невырожденной.