7. Законы больших чисел и предельные теоремы: неравенство Маркова, неравенство Чебышева, теорема Чебышева, центральная предельная теорема.

Законы больших чисел и предельные теоремы

Закон больших чисел (в широком смысле) – общий принцип, согласно которому, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и м.б. предсказан с большой степенью определенности.

Закон больших чисел (в узком смысле) – ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

Неравенство Маркова (лемма Чебышева)

Теорема. Если случайная величина X принимает только неотрицательные значения и имеет мат. ожидание, то для любого положительного числа А верно неравенство P(x>A) . (1)

Доказательство: проведем для дискретной случайной величины X. Расположим ее значения в порядке возрастания, из которых часть значений x , x ,…, x будут не более числа А, а другая часть - x ,…, x будут больше А, т.е.x <=A, x <=A,…, x <=A; x >A,…, x >A.

Запишем выражение для математического ожидания M(X):

x p + x p +…+ x p + x p +…+ x p =M(X)

где p , p ,…, p - вероятности того, что случайная величина Х примет значения соответственно x , x ,…, x .

Отбрасывая первые k неотриц. слагаемых получим x p +…+ x p <=M(X) (2)

Заменяя в неравенстве (2) значения x ,…, x меньшим числом А, получим более сильное неравенство A(p +…+ p )<=M(X) или p +…+ p <= .

Сумма вероятностей в левой части полученного неравенства представляет собой, сумму вероятностей событий X=x ,…X=x т.е. вероятность события X>A.

Поэтому P(X>A) <= .

Неравенство Чебышева

Теорема. Для любой случайной величины, имеющей мат. ожидание и дисперсию, справедливо неравенство Чебышева: P(|X-a|> )<= , (3) где a=M(X), >0. ( P(|X-a| ) 1 - - другая форма записи неравенства Чебышева, тоже правильная. Ее давал Герман)

Доказательство: Применим неравенство Маркова в форме (1) к случайной величине X’=(X-a) взяв в качестве положительного числа A= . Получим <= . (4)

Т.к. неравенство равносильно неравенству |X-a|> , а M(X-a) есть дисперсия случайной величины X, то из неравенства (4) получаем доказываемое неравенство (3).

Теорема Чебышева

Если дисперсии n независимых С.В. X , X ,…, X ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их мат. ожиданий (M (x₁) = a , M (x₂) = a ,…, a =M (x_n), т. е.

(5) или .

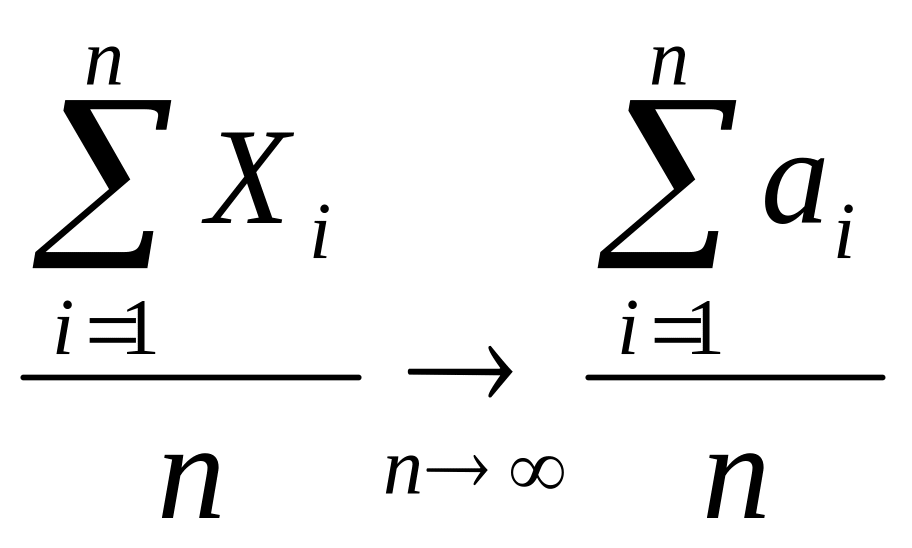Докажем формулу (5). По условию M(X )=a , M(X )=a ,…, M(X )=a ,

Возьмем такое С: D(X )<=C, D(X )<=C,…, D(X )<=C, где C - постоянное число.

Получим неравенство Чебышева для средней арифметической случайных величин, т.е. для X= . Найдем мат. ожидание M(X) и оценку дисперсии D(X)

M(X)=M( )= ;

D(X)=D( )= .

(Здесь использованы свойства математического ожидания и дисперсии, в частности, то, что случайные величины X , X ,…, X независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)

Применяем неравенство Чебышева(вариант Германа) для С.В - X=(X ,X ,…,X )/n; (6)

Т.к. по доказанному D(X) , то 1- , и от неравенства (6) перейдем к более сильному неравенству: (7)

В пределе при n величина стремится к нулю, и получим доказываемую формулу (5).

Центральная предельная теорема

Рассмотрим другую закономерность, возникающую в результате суммарного действия случайных величин. При некоторых условиях совокупное действие случайных величин приводит к определенному, а именно — к нормальному закону распределения. Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Теорема Ляпунова. Если . X , X ,…, X независимые С.В, у каждой из к-х существует мат. ожидание M(X )=a, дисперсия D(X )= , абсолютный центральный момент третьего порядка M(|X -a | )=m и . (80) , то закон распределения суммы Y =X +X +…+X при n неограниченно приближается к нормальному с математическим ожиданием и дисперсией .

В данном вопросе громоздкие, хотя и достаточно понятные доказательства теорем без к-х ответ окажется очень маленьким. Хотя по усмотрению, можете обойтись перечислением теорем если не успеваете.

8.Проверка статистических гипотез: принципы практической уверенности, статистическая гипотеза и общая схема её проверки, основная и альтернативная гипотезы, простая и сложные гипотезы, ошибки первого и второго ряда при проверке гипотезы, мощность критерия

Пусть имеется некоторая выборка значений случайной величины , функция распределения которой неизвестна. Статистической гипотезой называется любое предположение о распределении наблюдений, например, предположение о том, что функция распределения совпадает с некоторой наперед заданной функцией : (такая гипотеза называется простой), или о том, что функция распределения принадлежит некоторому параметрическому семейству распределений : (сложная статистическая гипотеза).

Если рассматривается всего 2 взаимоисключающие гипотезы, то одну из них принято называть основной (нулевой) и обозначать , а другую – альтернативной (противоположной), она обозначается . Обычно за принимается такая гипотеза, отвержение которой, когда она на самом деле верна, будет иметь наихудшие последствия по сравнению с теми, когда за выбирается другая гипотеза.

При проверке статистических гипотез используется принцип практической уверенности: «если вероятность события А в данном опыте весьма мала, то можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление; если же вероятность события близка к 1, то можно предполагать, что оно достоверно произойдет». Таким образом, при правильном выборе допустимого отклонения вероятности правильного решения о принятии или не принятии гипотезы мы можем на основании вероятностных данных делать выводы невероятностного характера (например, о свойствах случайных величин).

Типовые постановки задачи при проверке статистических гипотез:

1) ; другие предположения невозможны.

2) Простая основная гипотеза и сложная альтернатива .

3) Сложная основная гипотеза и сложная альтернатива .

4) Гипотеза однородности: имеется несколько выборок случайных величин с распределениями соответственно. Рассматриваются сложная основная гипотеза и альтернатива .

5) Гипотеза независимости: наблюдается пара случайных величин , имеем выборку . Рассматриваются сложная основная гипотеза и альтернативная ей гипотеза .

6) Гипотеза случайности: наблюдается случайных величин . Рассматривается сложная основная гипотеза и альтернативная ей гипотеза .

Пусть имеются гипотезы . Тогда статистическим критерием называется правило принятия одной из этих гипотез на основании имеющейся выборки, то есть отображение . Для заданного критерия будем говорить, что произошла ошибка -го рода, если гипотеза была отвергнута критерием в то время как она верна. Тогда вероятность ошибки -го рода для критерия равна .

Пусть рассматриваются две простые гипотезы . Тогда критерием будет отображение , делящее на два подмножества (критическая область) и :

Вероятность ошибки первого рода: .

//////////////////////////////////////////////

Пусть дана выборка из неизвестного совместного распределения , и поставлена бинарная задача проверки статистических гипотез:

где H0 — нулевая гипотеза, а H1 — альтернативная гипотеза. Предположим, что задан статистический критерий

,

сопоставляющий каждой реализации выборки одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:

Распределение выборки соответствует гипотезе H0, и она точно определена статистическим критерием, то есть .

Распределение выборки соответствует гипотезе H0, но она неверно отвергнута статистическим критерием, то есть .

Распределение выборки соответствует гипотезе H1, и она точно определена статистическим критерием, то есть .

Распределение выборки соответствует гипотезе H1, но она неверно отвергнута статистическим критерием, то есть .

Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]

		Верная гипотеза
		H0	H1
Результат  применения  критерия	H0	H0 верно принята	H0 неверно принята  (Ошибка второго рода)
	H1	H0 неверно отвергнута  (Ошибка первого рода)	H0 верно отвергнута

////////////////////////////////////////////////////////////////////

Мощностью критерия называется величина .

Несмотря на разнообразие самих гипотез и применяемых критериев, их можно объединить в следующую общую логическую схему:

1. Выдвижение гипотез и .

2. Выбор уровня значимости – вероятности ошибки первого рода. Эту величину называют также размером критерия. Выбор величины зависит от размера потерь, которые мы понесем в случае ошибочного решения.

3. Выбор критерия . Значение критерия является случайной величиной и в предположении справедливости нулевой гипотезы подчинено некоторому хорошо изученному закону распределения с плотностью .

4. Определение критической области исходя из следующего условия: . Из таблиц распределения находят квантили уровня и уровня , соответственно равные и . Они разделяют всю область возможных значений случайной величины на три части:

1 – область неправдоподобно малых ,

2 – правдоподобных ,

3 – неправдоподобно больших значений в условиях справедливости нулевой гипотезы . В тех случаях, когда опасными для нашего утверждения являются только односторонние отклонения, т. е. только «слишком маленькие» или только «слишком большие» значения критической статистики находят лишь одну квантиль: либо , либо которая будет разделять весь диапазон значений на две части.

5. Определение на основе выборочных данных численной величины статистики .

6. Выработка решения. Если , то гипотезу рекомендуется отклонить, в противном случае ее можно принять, т.к. имеющиеся данные не противоречат высказанной гипотезе.

Пусть , - плотности распределения критической статистики соответственно при справедливости нулевой гипотезы и альтернативной гипотезы , , - параметры распределения при и . Тогда ошибки первого и второго рода определяются выражениями и где - граница критической области .

Тогда мощность критерия .

9. Линейные пространства. Определение, примеры, простейшие свойства. Единственность нейтрального, единственность противоположного элемента. Линейная зависимость. Координаты векторов и их связь при переходе к другому базису.

Пусть – множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:

• паре элементов множества , отвечает элемент , называемый суммой и ;

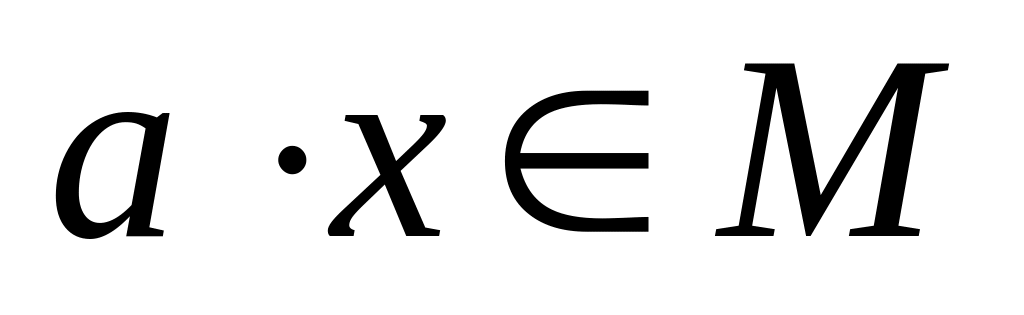• паре , отвечает элемент , называемый произведением числа и элемента .

Будем называть множество линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов и произвольных чисел справедливо:

1. , то есть сложение коммутативно;

2. , то есть сложение ассоциативно;

3. Существует нулевой элемент такой, что для любого ;

4. Для каждого элемента существует противоположный элемент такой, что ;

5. , то есть умножение на число ассоциативно;

6. для любого ;

7. , то есть умножение на число дистрибутивно относительно сложения элементов;

8. , то есть умножение вектора на число дистрибутивно относительно сложения чисел.

Равенства 1--8 называют аксиомами линейного пространства.

Наличие противоположного элемента позволяет ввести операцию вычитания, а именно разность определяется как сумма .

Линейное пространство часто называют векторным пространством,  а его элементы -- векторами.

Примеры линейного пространства:

1. Множество геометрических векторов (свободных направленных отрезков) в трехмерном пространстве с операциями сложения векторов и умножения вектора на число.

2. Множество функций одной переменной, непрерывных на отрезке c обычными операциями сложения функций и умножения функции на число;

3. Множество симметричных матриц второго порядка с обычными операциями сложения и умножения на число

Простейшие свойства линейных пространств:

1. Нейтральный элемент является единственным.

Доказательство: допустим, что существуют два нуля , полагая по аксиоме 3 и , получим , следовательно, .

2. Для любого противоположный элемент является единственным.

Доказательство: допустим, что у некоторого элемента имеется 2 различных противоположных элемента . Рассмотрим сумму . Прибавим к обеим частям этого равенства , и, используя аксиомы 2 и 3, получим: ; , таким образом .

3. для любого .

Доказательство: составим сумму и воспользуемся здесь аксиомами и теоремой 2: ; , таким образом .

4. для любых и .

5. для любого .

Линейной комбинацией элементов пространства мы будем называть сумму произведений этих элементов на произвольные вещественные числа: .

Система векторов называется линейно-зависимой тогда и только тогда, когда существуют числа , (из которых хотя бы одно отлично от нуля), такие, что .

Векторы, не являющиеся линейно-зависимыми, называются линейно независимыми, другими словами, векторы называются линейно независимыми, если равенство возможно только при .

Если векторы линейно зависимы и, например, , то , то есть если векторы линейно зависимы, то по крайней мере один из них является линейной комбинацией остальных. Очевидно, что верно и обратное.

Если в линейном пространстве существуют линейно независимых векторов, а любые векторов этого пространства линейно зависимы, то линейное пространство называется -мерным. Число называется размерностью пространства: . Если в линейном пространстве существуют линейно независимая система векторов из любого числа векторов, то оно называется бесконечномерным.

Совокупность линейно независимых векторов -мерного пространства называется его базисом.

Каждый вектор можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Доказательство: пусть – произвольный базис -мерного пространства и . Так как любые векторов -мерного пространства линейно зависимы, то зависимы, в частности, и векторы . Это означает, что существуют числа такие, что имеет место равенство: . При этом , ибо из условия следует . Но поскольку векторы линейно независимы, это возможно только при условии . Поэтому имеем вектор . Таким образом, любой вектор можно представить в виде линейной комбинации базисных векторов.

Докажем теперь единственность полученного разложения. Предположим, что существуют 2 разложения: и . Вычитая, получим . Но так как векторы линейно независимы, то это возможно только при условии , то есть , что и требовалось доказать.

Если векторы есть базис в -мерном пространстве и вектор , то числа называются координатами вектора в базисе . Предыдущая теорема означает, что при заданном базисе каждый вектор имеет в нем координаты, и притом однозначно определенные.

При сложении двух векторов пространства их координаты (относительно любого базиса) складываются. При умножении вектора на число все его координаты умножаются на это число.

Доказательство: пусть вектор имеет в базисе координаты , а вектор - координаты , то есть , . Тогда сумма будет иметь вид: , т.е. вектор имеет координаты . Вектор имеет вид .

Пусть и - два базиса в -мерном линейном пространстве .

Матрицей перехода от базиса к базису называется матрица , столбцами которой являются координаты векторов в базисе :

, .

Вектор линейно выражается через векторы обоих базисов. Тогда, если , то координаты вектора в базисе и его координаты в базисе связаны соотношениями

, ,

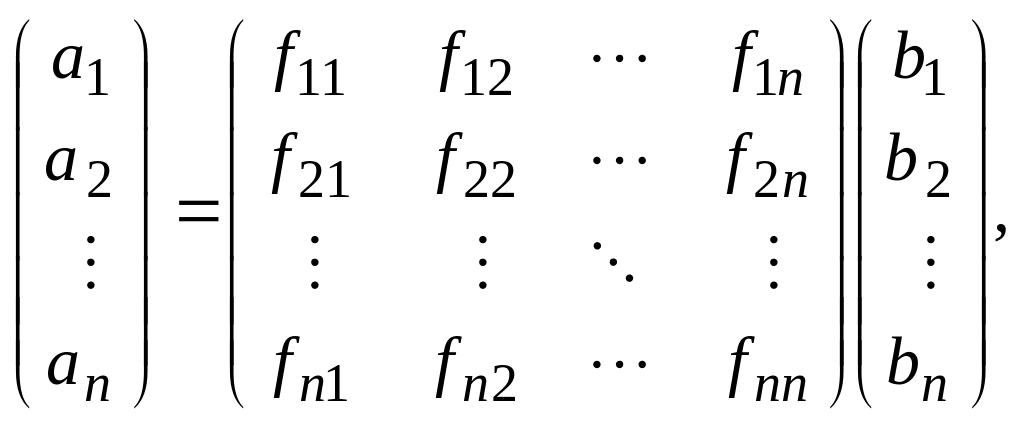
или , , где - матрица перехода от базиса к базису ; - векторы-столбцы координат вектора в соответствующих базисах.