3. Степенные ряды. Первая теорема Абеля. Параметры и радиус сходимости. Равномерная сходимость степенного ряда. Непрерывность суммы. Почленная дифференцируемость. Ряд Тейлора.
Степенные ряды.
Введём понятие степенного ряда
Степенным рядом называется функциональный ряд с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + …
члены которого есть произведения постоянных с0, с1, с2, …, сn, … на степенные функции с целыми показателями степеней от разности (z - z0).
Степенной ряд с центром в точке
:
,
где D –область.
- ряд с центром в точке z0
= 0 (1)
Введём понятие функционального ряда
Пусть существует последовательность функций f0(x), f1(x), …, fn(x), … . Функциональным рядом будем называть выражение вида f0(x) + f1(x) + … + fn(x) + … .
Теорема Абеля.
1)Пусть степенной ряд (1) сходится в точке
.Тогда
он сходится абсолютно в любой точке z,
для которой |
|<|
|,
и равномерно и абсолютно в любом круге
радиуса R:
2)Если степенной ряд (1) расходится в точке , тогда он расходится и во всех точках z таких, что |z|>| |.
Доказательство:
Необходимый признак сходимости ряда
(Не является достаточным):
при
По условию, ряд
сходится, следовательно,
.
Любая последовательность, имеющая
предел, ограничена, значит, существует
такое число M:
для всех n=0, 1,… (2)
Ряд (1) запишем в виде
Учитывая неравенства (2) найдем
,
т.к.
.
Здесь
,
поэтому последний ряд сходится, а это
означает, что сходится ряд
,
т. е. при |z|<|| исходный
степенной ряд (1) сходится абсолютно.
Если же z рассматривать
только из замкнутого круга
,
то
,
а это означает, что степенной ряд (1)
мажорируется сходящимся числовым рядом
и по признаку Вейерштрасса исходный
степенной ряд (1) сходится равномерно в
круге
Пусть теперь ряд (1) расходится в точке
.
Предположим, что в точке
такой, что |
|>|
|
ряд (1) сходится. Тогда по предыдущему
утверждению ряд (1) сходится и в точке
,
что противоречит условию. Итак, для
всех z таких, что |z|>|
|
ряд (1) расходится. [Теорема доказана]
Параметры и радиус сходимости
Сходимость: пусть есть ряд
а1+а2+…+аn+…
Его частичные
суммы: S1=a1,
S2=a1+a2
, …,Sn=
a1 +….+
an .
Ряд сходится if
,
где S конечно.
Из теоремы Абеля можно сделать заключение о характере области сходимости степенного ряда. Точка z=0 всегда лежит в области сходимости ряда (1). Если область сходимости отлична от одной точки z=0 и от всей плоскости (z), то существует круг радиуса R, называемый кругом сходимости степенного ряда (1), в каждой точке которого ряд (1) сходится абсолютно, а вне точек круга расходится.
Для определения радиуса круга сходимости используется либо признак Даламбера, либо признак Коши.
Для каждого фиксированного z
рассмотрим числовой ряд
(3) и применим к нему признак Даламбера.
Именно: если существует предел
(4) , то ряд (3) сходится, если
и расходится, если
.
Отсюда заключаем, что если выполнено
соотношение
,
то ряд (3) сходится абсолютно, а если
имеет место неравенство
,
то ряд (1) как и ряд (3), расходится.
Т.о., для определения радиуса круга
сходимости степенного ряда получаем
формулу
(5).
Если же к ряду (3) применим признак Коши то получим равенство
из которого заключаем, что ряд (3) сходится,
если
,
и расходится, если
.
Т.о., радиус круга сходимости R
ряда (1) определяется по формуле
.
(6) (формула Коши — Адамара.)
Радиус сходимости степенного ряда -
Rcx=
=
Критерий равномерной сходимости.
Для того, чтобы функциональный ряд(в
частности степенной ряд) сходился
равномерно в области D,
необходимо и достаточно, чтобы
и
:
при n>N
, p =0,1,2,3,…
Абсолютная сходимость: ряд а1+а2+…+аn+… сходится абсолютно, если сходится ряд |а1 |+|а2 |+…+|аn |+…
Непрерывность суммы
Свойство степенных рядов. Сумма степенного ряда есть функция, непрерывная на интервале сходимости ряда. S(z) = z0 + a1z + a2z2 + … + anzn + …
Причём, в том конце интервала, где степенной ряд сходится, его сумма S(x) остаётся односторонне непрерывной.
Почленная дифференцируемость
Теорема1:. Cтепенной ряд внутри интервала сходимости (|z|<R) имеет сумму S(x), к-я дифференцируема сколь угодно много раз. Степенной ряд можно почленно дифференцировать любое число раз, причем радиус круга сходимости продифференцированных рядов также равен R.
S(x)= с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + …
S’(x)= с1 + с2 *2*(z – z0) + … + сn *n*(z – z0)n-1 + …
Ряд Тейлора
Имеем степенной ряд . Обозначим через f(z) его сумму. Сходится в круге |z - |<R.
называется рядом Тейлора функции
f(z) по
степеням (z-
).
Из почленной дифференцируемости имеем,
что радиус сходимости тот же.
-
эти выражения называются коэффициентами
Тейлора функции f(z)
в точке
.
В случае
=0
этот ряд называется также рядом
Маклорена функции f(z).
4. Первообразная и неопределённый интеграл. Определение первообразной. Определение неопределённого интеграла, его свойства. Определение интеграла по Риману. Необходимые и достаточные свойства интегрируемости. Формула Ньютона-Лейбница.
Пусть определены функции f(x) и F(x). F(x) – первообразная f(x), если F’(x) = f(x). F(x) + c – тоже первообразная f(x).
Неопределенный интеграл:
- множество всех первообразных f(x).
Свойства неопределенного интеграла:
1)
2) d
3)
4)
,
где с – const
Определение интеграла по Риману
Пусть функция y=f(x) определена на отрезке [a; b], a<b. Выполним следующие действия:
1. С помощью точек
=a,
,
,…,
=b
(
<
<
<…<
)
разобьем отрезок [a; b]
на n частичных отрезков
[
,
],
[
,
],…,
[
,
]
2. В каждом частичном отрезке [
,
],
i=1, 2,…, n
выберем произвольную точку c
и вычислим значение функции в ней, т. е.
величину
.
3. Умножим найденное значение функции
на длину
соответствующего частичного отрезка:
*
.
4.Сост. сумму S всех таких произведений.:
(1)
Сумма вида (1) называется интегральной
суммой функции y=f(x)
на отрезке [a; b].
Обозначим через
длину наибольшего частичного отрезка
.
5. Найдем предел интегральной суммы (1),
когда n
так, что
.
Если при этом интегральная сумма
имеет предел I, который
не зависит ни от способа разбиения
отрезка [a; b]
на частичные отрезки, ни от выбора точек
в них, то число I называется
определенным интегралом от функции
y=f(x)
на отрезке [a,b]
Т.о.,
=
(2)
Необходимые и достаточные условия интегрируемости
Введём понятие верхней и нижней суммы
Дабру. Пусть функция f(x)
определена на отрезке [a;
b],
разбиение этого отрезка
.
Положим
(т.е.
Mk максимальное значение
функции на отрезке [k-1;k]),
m
(mk - минимальное), k=1,
2,…, k
(3)
S
=
S
(f)=
,
s
=
s
(f)=
.
(4)
Сумма S
называется верхней, а сумма s
- нижней суммой Дарбу функции f.
В случае, когда функция f
ограничена, то нижние
и верхние
грани (3) конечны, и потому суммы Дарбу
(4) при любом разбиении принимают конечные
значения.
Теорема. Для того чтобы ограниченная
на некотором отрезке функция была
интегрируема на нем, необходимо и
достаточно, чтобы суммы Дарбу S
и s
этой функции удовлетворяли условию
(5)
Следствие. Для того чтобы ограниченная
на отрезке [a; b]
функция f была на нем
интегрируема, необходимо и достаточно,
чтобы
(6)
где
- разбиение отрезка [a; b],
а
- колебание функции f на
отрезке
,
k=1, 2,…, k
.
Формула Ньютона-Лейбница
Пусть функция y=f(x) интегрируема на отрезке [a; b].
Теорема. Если функция y=f(x)
непрерывна на отрезке [a;
b] и F(x)
- какая-либо ее первообразная на [a;
b] (F’(x)=f(x)),
то имеет место формула
Доказательство:
Пусть на отрезке [a;b]
задана интегрируемая функция f(x).
Зададим произвольное значение
.
Пусть функция F(x)- какая-нибудь первообразная
для заданной функции f(x). Тогда она может
быть получена по формуле
.Таким
образом, учитывая, что C=F(a),
имеем:
.
Пологая теперь x=b получаем:
.
Откуда:
5. Основные понятия теории вероятности: классификация событий. Классические определения вероятности. Геометрические определения вероятности. Теоретико-множественная трактовка основных понятий и аксиоматическое построение теории вероятности.
Теорией вероятности наз. мат. наука, изучающая закономерности в случайных событиях.
Классификация событий:
Событие – всякий факт, который может произойти в результате некоторого опыта.
Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Его вероятность равна 1 (P=1).
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий. Его вероятность равна 0 (P=0).
Случайное событие – такое событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти (0<P<1).
Два события называются совместными, если появление одного из них не исключает появления другого.
Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Противоположные события – событие А называют противоположным B, если результат его противоположен результату B. P(A) + P(B) =1
Классическое определение вероятности:
вероятность есть число, характеризующее
степень возможности появления события.
Каждый возможный результат – элементарный
исход. Те элементарные исходы, в кот.
интересующее нас событие наступает,
называются благоприятствующими исходами.
Т.о., событие А наблюдается, если в
испытании наступает один, безразлично
какой, из элементарных исходов,
благоприятствующих А. Вероятностью
события А называется отношение числа
благоприятствующих этому событию
исходов к общему числу всех равновозможных
несовместных элементарных исходов,
образующих полную группу. P(A)=
,
m – число элементарных
исходов, благоприятствующих А;
n – число всех возможных элементарных исходов.
Недостаток классического определения вероятности – оно неприменимо к испытаниям с бесконечным числом исходов. Для преодоления этого недостатка вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l определяется равенством:
P=
.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
P=
.
Аксиоматическое построение теории вероятности.
Введем поле J элементарных
событий, т.е. множество событий для к-х
определены вероятности.
-пространство
элементарных событий. J
.
Аксиомы:
1) любому
соответствует
некоторое неотрицательное число P(A)
(вероятность этого события), причем P(A)
может быть - 0<=P(A)<=1;
2) P( ) = 1 – достоверное событие;
3) Аксиома сложения вероятностей: Вероятность объединения несовместных событий равна сумме их вероятностей.
Объединением нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей.
Вероятность появления 1 из 2 несовместных
событий равна сумме вероятностей этих
событий. P(A+B)=P(A)+P(B);m
-A,
m
-B.
m
+
m
- число благопр. исходов или A
или B.
P(A+B)=
=
+
=P(A)+P(B).(из
классического определения вероятности)
Вероятность появления одного из нескольких попарно-несовместных событий равна сумме вероятностей этих событий. P(A +A +…+A )=P(A )+P(A )+…+P(A ).
Сумма вероятностей A , A ,…, A , образующих полную группу несовместных событий, всегда равна 1.
События называются полной группой if
.
Условная вероятность. Вероятность
наступления события А, зависящего от
наступления события B
называется условной вероятностью -
P(A|B)
=
(P(B)
0).
Если события независимы (P(A|B)=P(A),
P(B|A)=P(B)),
то их вероятности безусловные.
Теорема умножения вероятностей.
Произведение событий. (A*B) – совместное появление этих событий.
Вероятность совместного появления 2 событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную, предположив, что первое событие уже наступило. P(A*B)=P(A)*P (B|A) = P(B)*P(A|B). Для независимых событий P(A*B)=P(A)*P(B).
Вероятность появления нескольких событий равна произведению вероятности одного из них на условную вероятность всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
P(A , A ,…,A )=P(A )*P (A |A1)+…+P (A |A1A2….An-1).
6. Случайная величина. Законы распределения случайной величины. Математическое ожидание и дисперсия случайной величины: определение, свойства. Вычисление математических ожиданий и дисперсий распределений: биноминального, Пуассона, нормального.
Случайной называется величина, которая в результате опыта может принять то или иное значение (только одно), причем до опыта неизвестно, какое именно. Пространство её значений – вероятностное пространство С.В(случайной величины). Существуют 3 типа С.В.: дискретные, непрерывные, непрерывно-дискретные. Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное (счетное множество). Непрерывной - возможные значения к-й непрерывно заполняют некоторый интервал на числовой оси. Непрерывно-дискретная – С.В, значения к-й непрерывно заполняют отдельные интервалы на числовой оси.
Так же С.В. могут быть классифицированы:
a)скалярные(X), векторные(X1,X2,…,Xn).
б)действительные, комплексные.
Закон распределения дискретной С.В..
P =P(X=x ); P =P(X=x ); …; P =P(X=x ).
Сумма вероятностей всех значений равна 1. Законом распределения С.В. называется любое правило (таблица, функция), устанавливающее связь между возможными значениями С.В.(X) и соответствующими вероятностями. Для непрерывной С.В. – правило, функция. (табл. быть соответственно не может в силу непрерывности). Законы – F(x), f(x).
Функция распределения вероятности. F(x)
Функцией распределения С.В. X называется вероятность того, что она примет значения, меньшие, чем x: F(x)=P(X<x).
Свойства функции распределения.
1) Функция распределения есть неубывающая функция своего аргумента. x >x , F(x )>F(x ).
2) F(- )=0.
3) F(+ )=1.
4) Функция распределения есть неотрицательная функция 0<=F(x)<=1.
5) Вероятность появления случайной
величины в интервале (
;
)
равна разности значений функции
распределения в концах интервалов.
P(
<=x<=
)=F(
)
- F(
).
6) Непрерывна слева
7) Функция распределения дискретной С.В. разрывна и возрастает скачками. (графически выглядит как лестница)
8)Непрерывна для непрерывной С.В.
Плотность распределения вероятности. f(x)
Плотность характеризует распределение
только непрерывной С.В.. Будем считать
С.В. непрерывной, если ее функция
распределения дифференцируема.
P(x<X<x+
x)
= F(x+
x)
– F(x).
;
=
=F’(x).
f(x) = F’(x).
Плотность распределения С.В.– производная ее функции в данной точке. Плотность указывает на то, как часто появляется С.В. X в некоторой окрестности точки x при повторении опытов.
Св-ва:
1)F(x) =
2)F(+
)
=1
3)f(x)
0
4) P(a<X<b) =
Числовые характеристики С.В..
Мат. ожиданием дискретной С.В. называют сумму произведений всех ее возможных значений на их вероятности.
Пусть X принимает значения x , x ,…, x , вероятности к-х соответственно равны p , p ,…, p .
M(X)= x
p
+
x
p
+…+
x
p
=
.
Мат.ожидание непрерывной С.В.
Пусть непрерывная С.В X
задана плотностью распределения f(x).
Допустим, что все возможные значения X
принадлежат отрезку [a;
b]. Разобьем этот отрезок
на n частичных отрезков
длиной
,
,…,
и выберем в каждом из них произвольную
точку x
(i=1, 2,…, n).
Определим мат. ожидание непрерывной
величины по аналогии с дискретной;
составим сумму произведений возможных
значений x
на вероятности попадания их в интервал
:
.
Перейдем к пределу:
=
;
M(X)=
.
Свойства математического ожидания:
1. Мат. ожидание постоянной величины равно самой постоянной M(C)=C.
2. Постоянный множитель можно выносить за знак мат.ожидания M(CX)=CM(X).
3. Мат.ожидание произведения двух независимых С.В. равно произведению их мат.ожиданий M(XY)=M(X)M(Y).
4. Мат.ожидание суммы двух С.В. равно сумме мат. ожиданий слагаемых M(X+Y)=M(X)+M(Y).
Дисперсией дискретной С.В.
называют мат.ожидание квадрата отклонения
случайной величины от ее мат. ожидания:
D(X)=M[X-M(X)]
.
По определению дисперсии:
D(X)=M[X-M(X)] =[x -M(X)] p +[x -M(X)] p +…+[x -M(X)] p .
Дисперсия равна разности между мат. ожиданием квадрата С.В. X и квадратом ее мат. ожидания. D(X)=M(X )-[M(X)] .
D(X)=M[X-M(X)] =M[X -2XM(X)+M (X)]= M(X )-2M(X)M(X)+ M (X)= =M(X )-2M (X)+M (X)= M(X )- M (X)= M(X )-[M(X)] .
Дисперсией непрерывной случайной
величины называют мат.ожидание квадрата
ее отклонения. Если возможные значения
X принадлежат отрезку [a;
b], то D(X)=
(a и b могут
быть
и -
соответственно)
Свойства дисперсии:
1. Дисперсия постоянной величины C равна 0 D(C)=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(CX)= C D(X).
3. Дисперсия суммы(разности) двух
независимых С.В. равна сумме(разности)
дисперсий этих величин D(X
Y)=D(X)
D(Y).
4. D(X)=M(X )-[M(X)] .
D(X)=M[X-M(X)] =M[X -2XM(X)+M (X)]= M(X )-2M(X)M(X)+ M (X)= =M(X )-2M (X)+M (X)= M(X )- M (X)= M(X )-[M(X)] .
Вычисление мат.ожидания и дисперсии при биномиальном распределении.
X |
0 |
1 |
2 |
… |
n |
p |
p |
p |
p |
… |
p |
/////////////////////на всякий случай вывод для тех, кому очень интересно
Формула распределения:
P (m) =
По определению, математическое ожидание случайной величины вычисляется по формуле:
где
x i - значения случайной величины x ,
p i
- вероятности
событий
.
Для закона распределения случайной величины мы получим:
Поскольку
,
то
Окончательно:
Для дисперсии, по определению, имеем:
.
получим:
///////////////////////////////////////////////////////////////
p
(k)=C
p
q
.
M(x)=np. D(x)=npq.
Вычисление мат. ожидания и дисперсии при распределении Пуассона.
X – число появлений события A в n независимых испытаниях.
///////////////////////////////////////////////////////////// на всякий случай вывод для тех, кому очень интересно
Рассмотрим второй случай асимптотического
приближения биномиального распределения,
когда
,
а
–
имеет конечное значение. Случайная
величина
называется
распределенной по закону Пуассона с
параметром
,
если эта случайная величина может
принимать значения
,
соответствующая вероятность которых
определяется по формуле Пуассона, когда
:
.
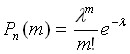В биномиальном распределении величина
имеет
смысл математического ожидания. Проведем
вычисления математического ожидания
для распределения Пуассона:
.
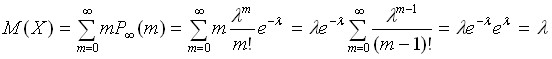Таким образом, в распределении Пуассона величина также имеет смысл математического ожидания.
Проведем вычисления дисперсии для распределения Пуассона:
,
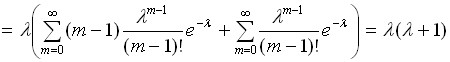поскольку
,
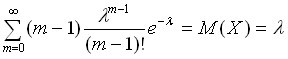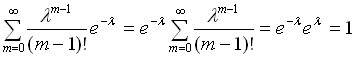
Таким образом, в распределении Пуассона
дисперсия также равна
///////////////////////////////////////////////////////////
P
(k)=
;
– параметр распределения;
=np;
M(x)= D(X)=
.
Вычисление мат.ожидания и дисперсии при нормальном законе распределения.
Нормальным называют распределение
вероятностей непрерывной С.В., которое
описывается плотностью f(x)=
.
Нормальное распределение определяется
двумя параметрами: a и
.
Достаточно знать эти параметры, чтобы
задать нормальное распределение.
M(X)=a. D(X)= .