Задачи для самостоятельного решения

1. Определить таблицу истинности булевой функции:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к)

2. Используя таблицы истинности, проверить эквивалентность булевых формул. Определить существенные и фиктивные переменные.

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и)

3. Решить систему уравнений

а)

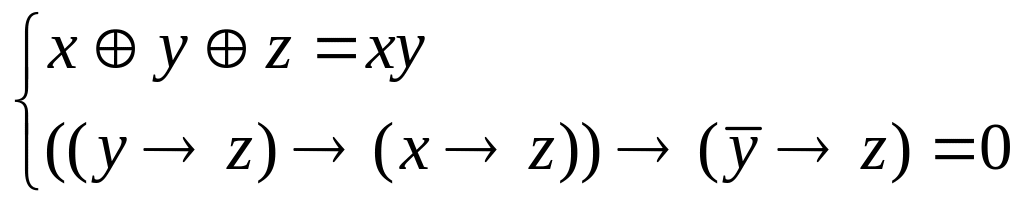
б)

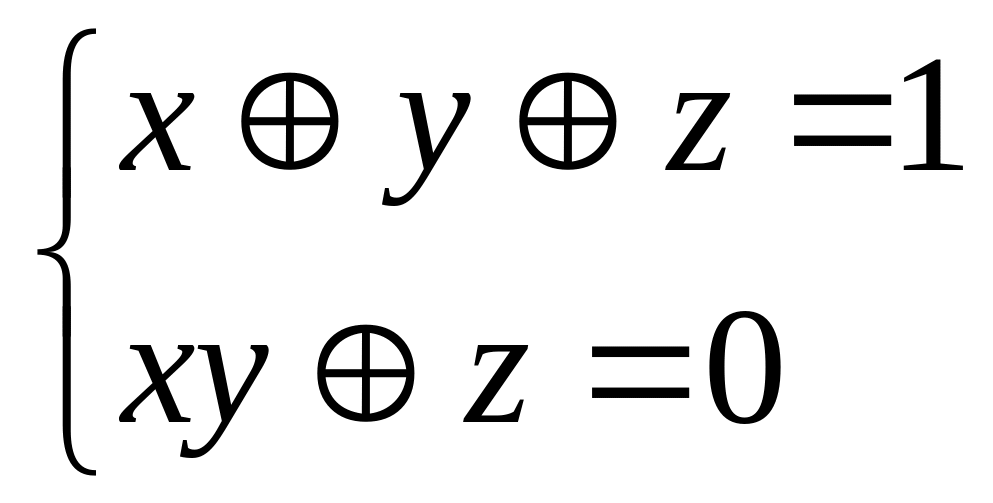
в)

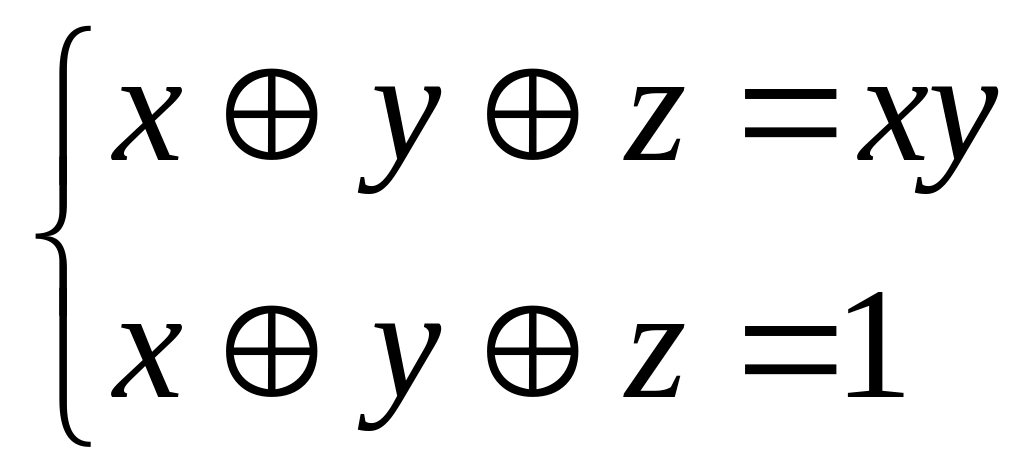
Практическое занятие №3

Нормальные формы. Минимизация нормальных форм [6].

Цель занятия: уметь строить СДНФ и СКНФ, сокращённую ДНФ, тупиковую и минимальную ДНФ, минимальную КНФ по таблице истинности.

План занятия:

1. Совершенная дизъюнктивная нормальная форма (СДНФ).

2. Совершенная конъюнктивная нормальная форма (СКНФ).

3. Минимизация дизъюнктивных и конъюнктивных нормальных форм.

Методические указания по изучению темы

Как известно, для любой булевой функции можно построить её таблицу истинности. Но и по таблице истинности можно восстановить булеву функцию.

Совершенная дизъюнктивная нормальная форма.

Возьмём наборы переменных, на которых функция равна 1. Если значение переменной в этом наборе равно 0, то эта переменная берётся с отрицанием. Если значение переменной в этом наборе равно 1, то эта переменная берётся без отрицания. Соединив все переменные, соответствующие этому набору, знаком &, мы получим элементарную конъюнкцию. Тогда дизъюнкция всех элементарных конъюнкций, соответствующих наборам значений переменных, где функция равна 1, и восстанавливает исходную функцию. Это совершенная дизъюнктивная нормальная форма (СДНФ) данной функции.

Пример(*).

Построить СДНФ для функции, таблица истинности которой имеет вид:

x	y	z	f (x,y,z)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

Решение: Функция принимает значение 1 на наборах 001, 010, 101. Набору 001 соответствует элементарная конъюнкция . Набору 010 соответствует элементарная конъюнкция . Набору 101 соответствует элементарная конъюнкция . Тогда совершенная дизъюнктивная нормальная форма (СДНФ) .

Совершенная конъюнктивная нормальная форма.

Возьмём наборы переменных, на которых функция равна 0. Если значение переменной в этом наборе равно 0, то эта переменная берётся без отрицания. Если значение переменной в этом наборе равно 1, то эта переменная берётся с отрицанием. Соединив все переменные, соответствующие этому набору, знаком , мы получим элементарную дизъюнкцию. Тогда конъюнкция всех элементарных дизъюнкций, соответствующих наборам значений переменных, где функция равна 0, и восстанавливает исходную функцию. Это совершенная конъюнктивная нормальная форма (СКНФ) данной функции.

Пример.

Построить СКНФ для функции из предыдущего примера (*).

Решение: Функция принимает значение 0 на наборах 000, 011, 100, 110, 111.

Набору 000 соответствует элементарная дизъюнкция .

Набору 011 соответствует элементарная дизъюнкция .

Набору 100 соответствует элементарная дизъюнкция .

Набору 110 соответствует элементарная дизъюнкция .

Набору 111 соответствует элементарная дизъюнкция .

Тогда совершенная конъюнктивная нормальная форма (СКНФ)

.

Замечание. При построении СДНФ требуется, чтобы функция была отлична от тождественного нуля. При построении СКНФ функция не должна быть равной тождественной единице.

Очень часто СДНФ и СКНФ, которые строятся по таблице истинности, оказываются весьма сложными. Поэтому возникает проблема построения минимальных нормальных форм для данной функции.