
- •Волгоградский кооперативный институт (филиал)
- •Дискретная математика
- •Содержание
- •Введение
- •Цели и задачи освоения учебной дисциплины
- •1. Тематический план
- •Размещения
- •Понятие факториала
- •Перестановки
- •Сочетания
- •Пример.
- •Пример.
- •Перестановки с повторениями
- •Бином Ньютона
- •Задачи для самостоятельного решения
- •Эквивалентность булевых формул.
- •Основные эквивалентности.
- •Задачи для самостоятельного решения
- •Совершенная конъюнктивная нормальная форма.
- •Минимизация дизъюнктивных нормальных форм
- •Сокращённая днф
- •Алгоритм построения сокращённой днф с помощью скнф.
- •Тупиковые и минимальные днф.
- •Алгоритм построения тупиковых и минимальных днф функции f.
- •Минимизация конъюнктивных нормальных форм
- •Минимизация в классе нормальных форм
- •Задачи для самостоятельного решения
- •Эйлеров цикл
- •Задачи для самостоятельного решения
- •Введя подходящие обозначения вершин, для каждого из графов подберите соответствующую матрицу смежности из перечисленных ниже:
- •Практическое занятие № 5 Деревья. Планарные графы. Непланарность графов и .
- •Методические указания по изучению темы
- •Код дерева [6]
- •Задачи для самостоятельного решения
- •Вопросы для подготовки к зачёту
- •Литература а) основная литература:
- •Б) дополнительная литература:
- •Дискретная математика
- •4 00002, Г. Волгоград, ул. Новосибирская, 76
Задачи для самостоятельного решения
Вычислить:
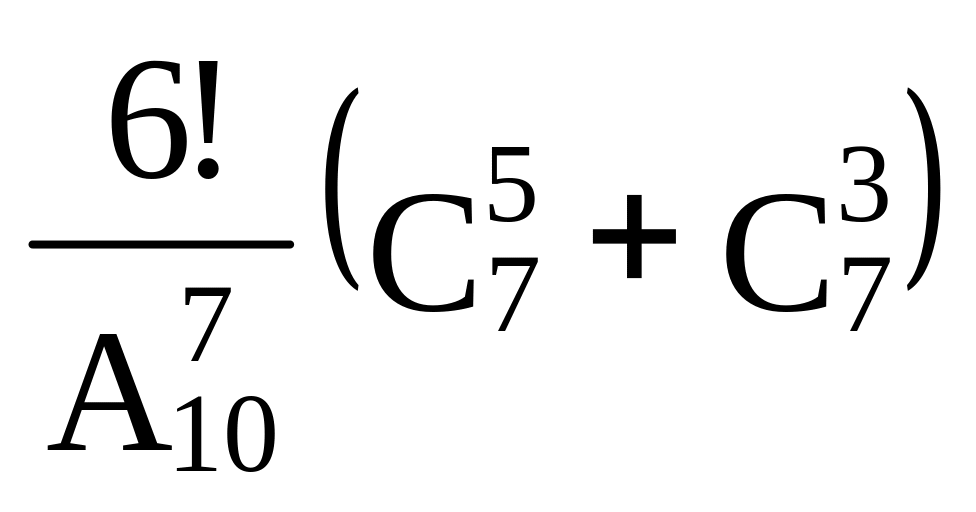
Вычислить:
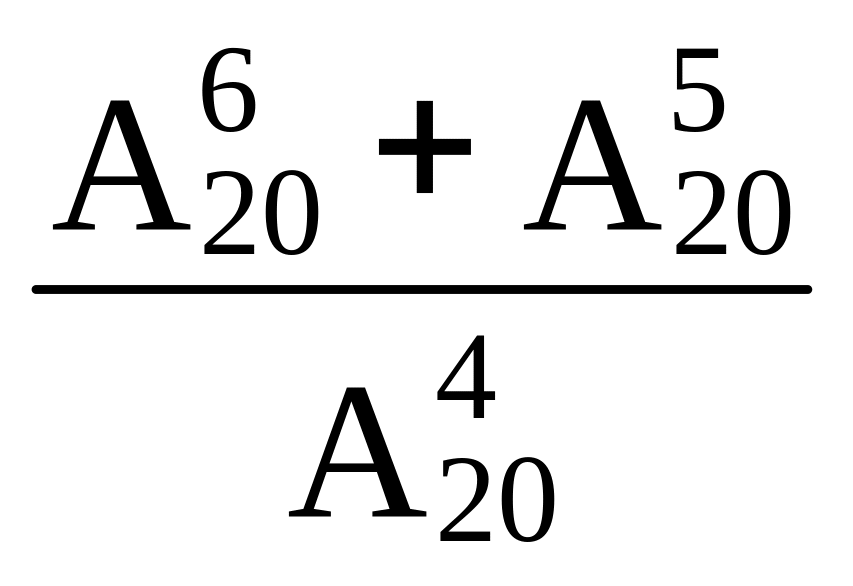
Вычислить:

Найти n, если 5Сn3 =
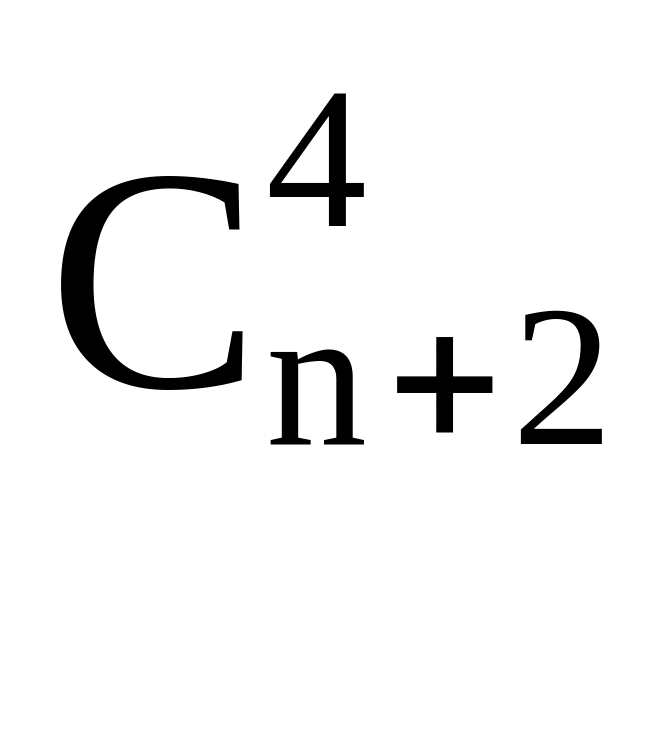
Найти n, если

Найти n, если
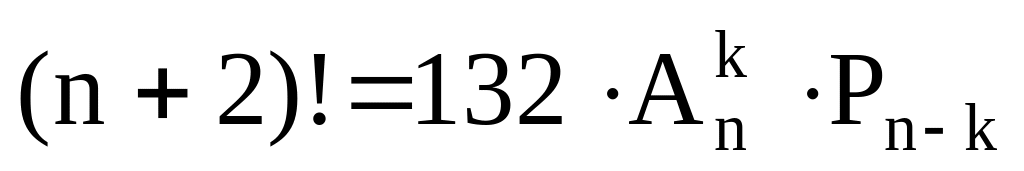
Найти n, если

Найти n, если
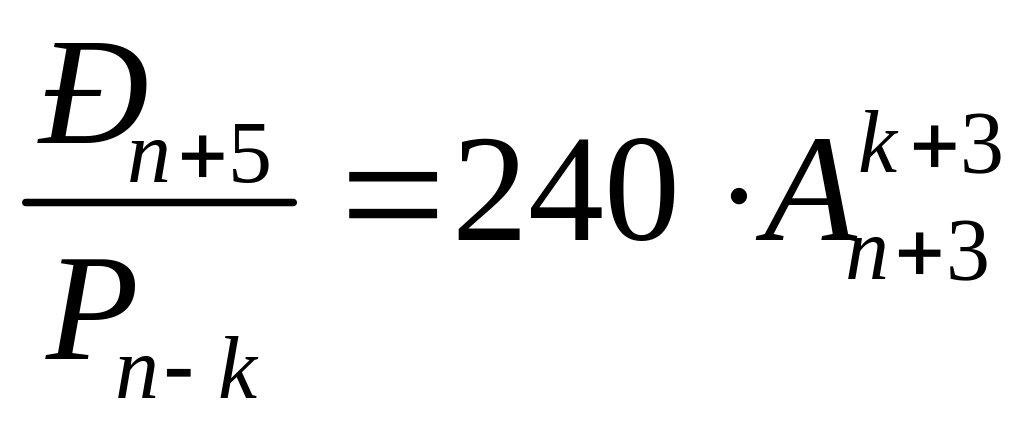 ,
k
,
k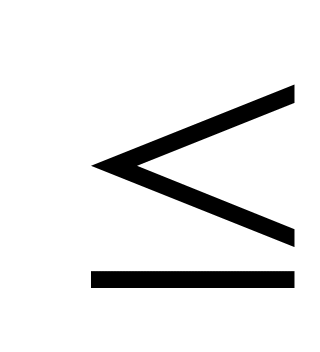 n
n
Решить уравнение
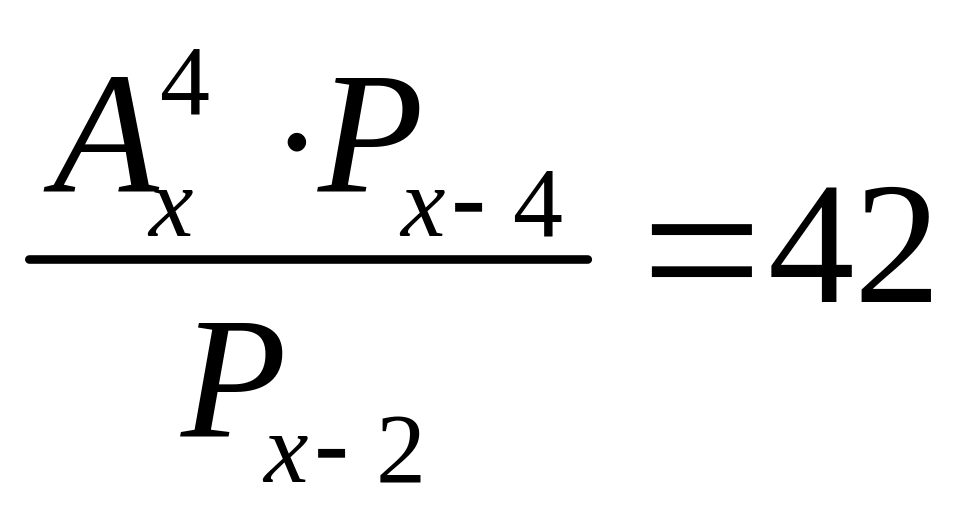
Решить систему

Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?
Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?
В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?
Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?
Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?
В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?
В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?
На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?
В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?
Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?
Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?
Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?
В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»?
Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?
Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?
На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.
Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?
Сколько существует различных семизначных телефонных номеров?
Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?
При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?
В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.
Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. ( Обмен происходит по одной марке ).
У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?
Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?
Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?
В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?
Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
Определить разложение
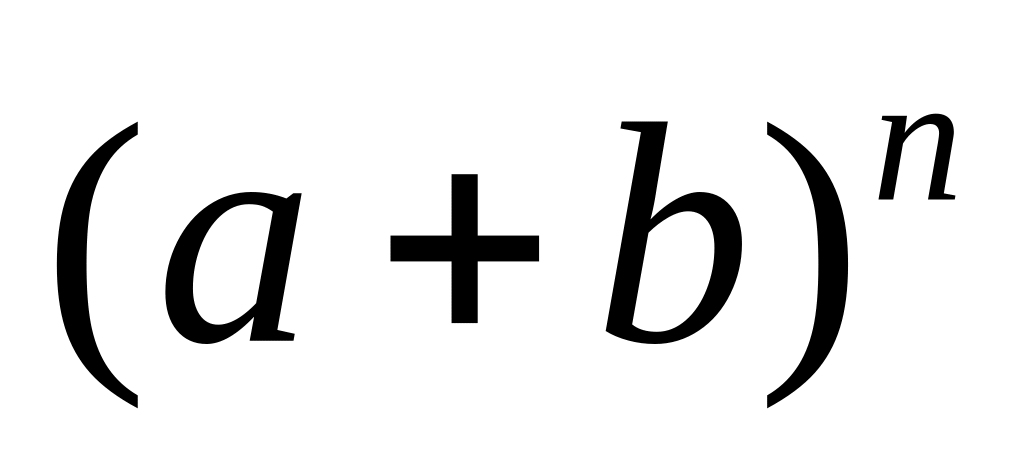 при
n=5.
при
n=5.Определить разложение при n=8.
Найти член разложения
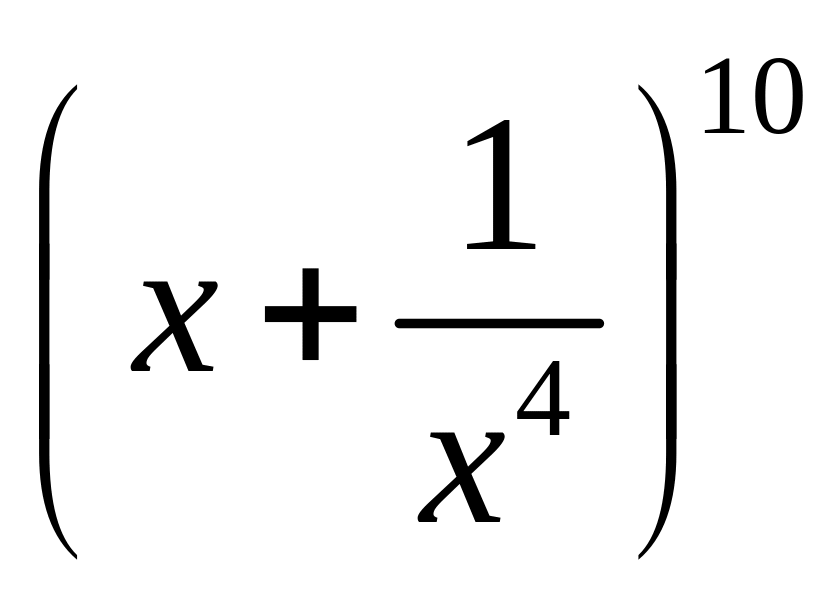 ,
не содержащий x
(то есть содержащий x
в нулевой степени).
,
не содержащий x
(то есть содержащий x
в нулевой степени).Найти шестой член разложения
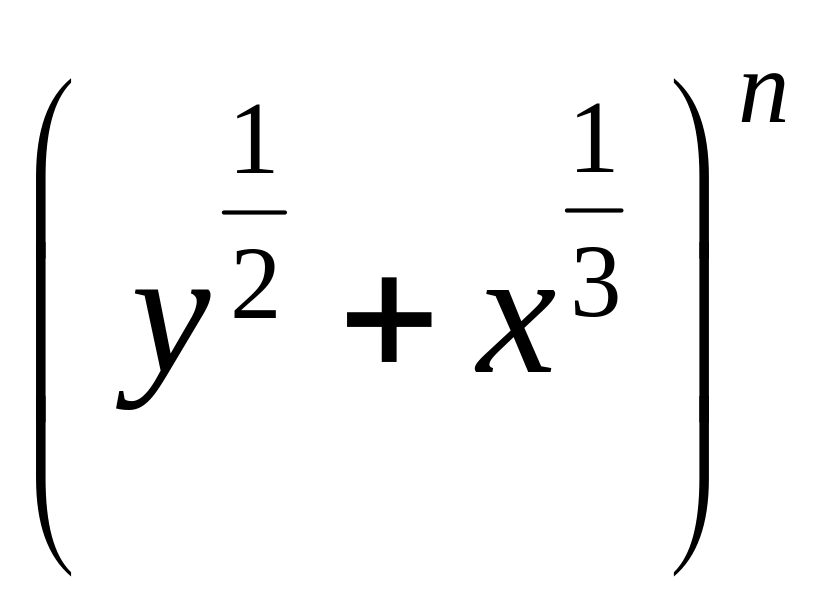 ,
если биномиальный коэффициент третьего
от конца члена равен 45.
,
если биномиальный коэффициент третьего
от конца члена равен 45.
В разложении
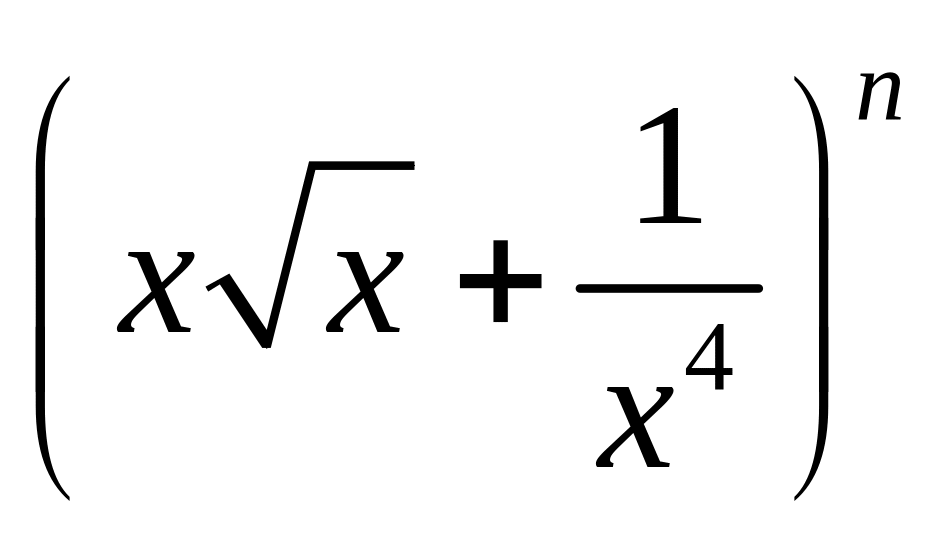 коэффициент
третьего члена на 44 больше коэффициента
второго члена. Найти свободный член,
то есть член разложения, не зависящий
от x
(членом, не зависящим от x,
будет тот, который содержит x
в нулевой степени).
коэффициент
третьего члена на 44 больше коэффициента
второго члена. Найти свободный член,
то есть член разложения, не зависящий
от x
(членом, не зависящим от x,
будет тот, который содержит x
в нулевой степени).
В разложении бинома
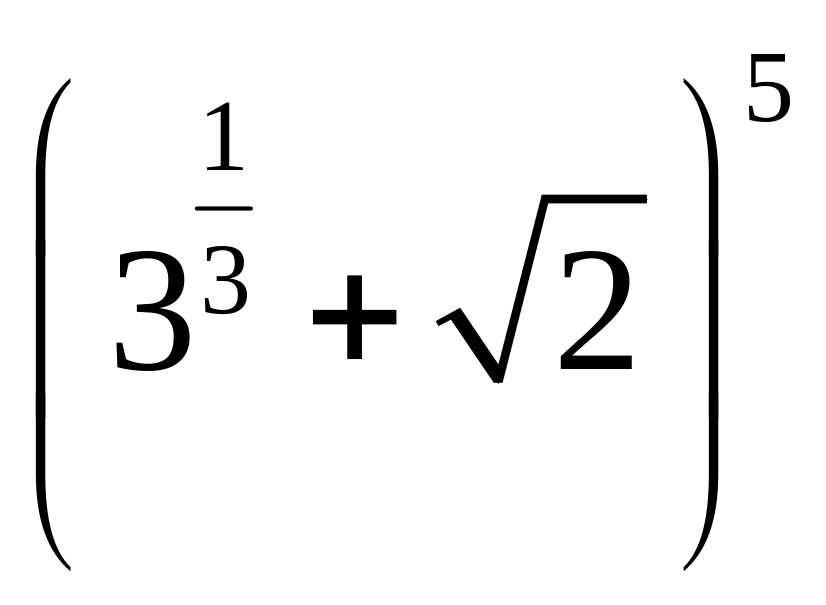 найти
члены, не содержащие иррациональности.
найти
члены, не содержащие иррациональности.Найти номер того члена разложения
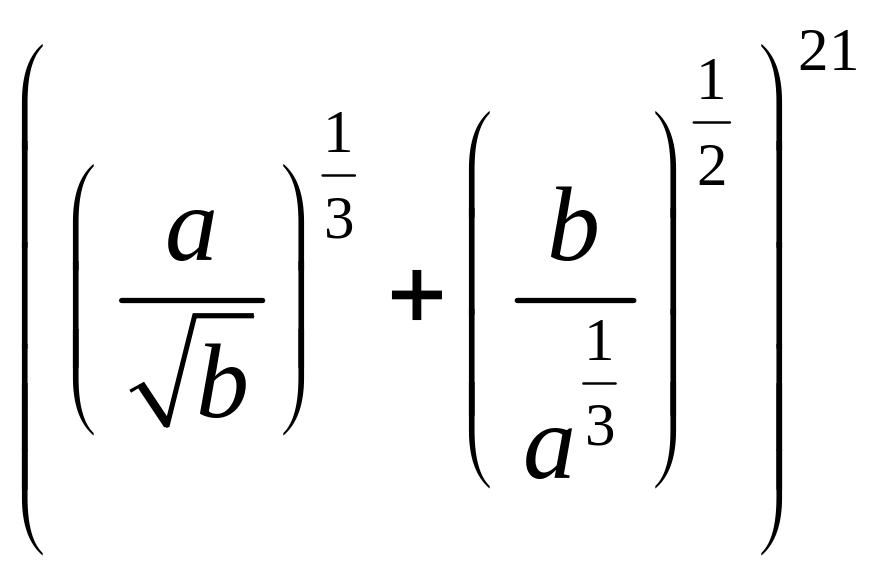 ,
который содержит a
и b
в одинаковых степенях.
,
который содержит a
и b
в одинаковых степенях.
Практическое занятие №2
(интерактивное занятие в малых группах)
Булевы функции
Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные.
План занятия:
Основные операции
Булевы функции от n переменных
Основные эквивалентности
Формулы
Методические указания по изучению темы
Функция, определённая на множестве Е={0,1} и принимающая значения из этого множества, называется булевой.
Значение функции можно задать с помощью таблицы истинности, которая показывает, чему равна функция на всех возможных комбинациях значений её переменных.
Отрицание
(инверсия)![]() .
Таблица истинности этой функции имеет
следующий вид:
.
Таблица истинности этой функции имеет
следующий вид:
|
|
0 |
1 |
1 |
0 |
Мы видим, что отрицание меняет возможные значения переменной на противоположные.
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Дизъюнкция равна 1, если хотя бы один из её аргументов равен 1.
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Конъюнкция равна 1 тогда и только тогда, когда оба её аргумента равны 1.
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Импликация равна
1, то есть (
)
=1 тогда и только тогда, когда
![]() .
.
Эквивалентность
(эквиваленция)
![]() .
Таблица истинности этой функции имеет
следующий вид:
.
Таблица истинности этой функции имеет
следующий вид:
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Эквивалентность
равна 1, то
есть
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
С помощью введённых операций можно строить различные булевы функции. Порядок выполнения операций указывается скобками. Для упрощения записи принят ряд соглашений:
для отрицания скобки опускаются;
& имеет приоритет перед
 ,
~, →;
,
~, →;имеет приоритет перед →, ~;
Любая булева функция полностью определяется своей таблицей истинности.
Пример.
Определить таблицу
истинности булевой функции
![]() .
.
Решение:
-
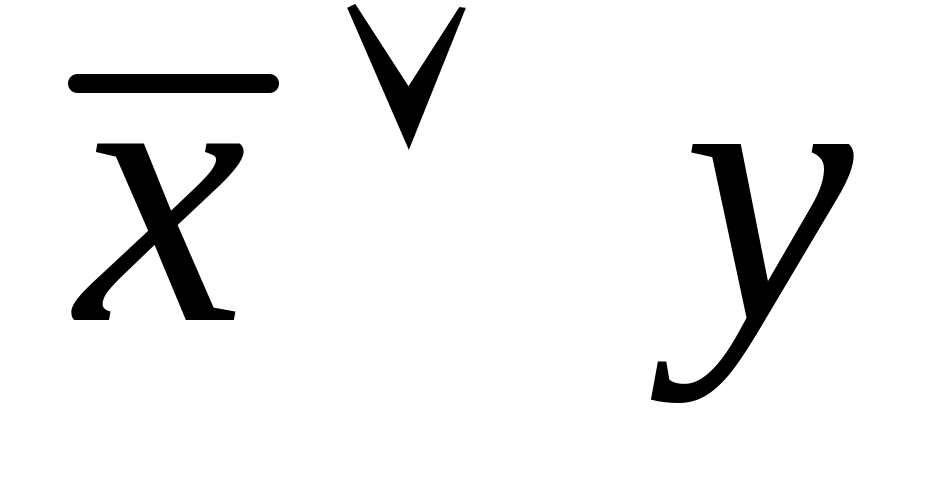

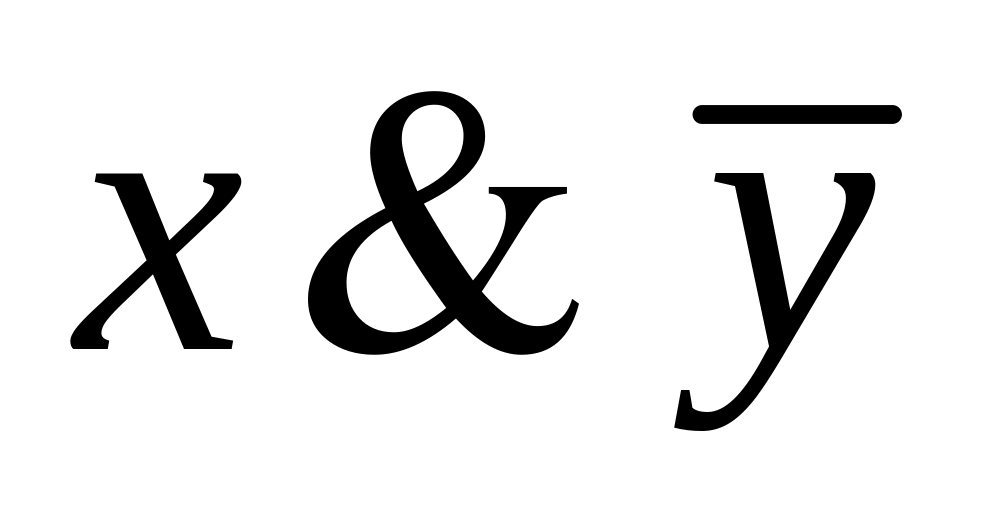
0
0
1
1
1
0
1
0
1
1
1
0
0
1
1
0
0
0
1
1
0
1
1
0
1
0
0
1
Обозначим через
![]() множество всех
булевых функций.
множество всех
булевых функций.
Теорема.
Число булевых функций от n
переменных равно
![]() .
.
Пример.
Число булевых
функций от n
= 2 переменных равно
![]() .
.
Все они указаны в таблице.
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
![]() ( тождественный
нуль);
( тождественный
нуль);
(![]() конъюнкция);
конъюнкция);
![]() (сложение по модулю 2);
(сложение по модулю 2);
![]() (дизъюнкция);
(дизъюнкция);
![]() (стрелка Пирса);
(стрелка Пирса);
![]() (эквивалентность);
(эквивалентность);
![]() (импликация);
(импликация);
![]() (штрих Шеффера);
(штрих Шеффера);
![]() (тождественная
единица).
(тождественная
единица).
Иногда при задании
булевой функции ограничиваются указанием
её набора значений. Например,
![]() .
.
