Перестановки с повторениями
Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями
где
Пример.
Сколько различных перестановок букв можно сделать в слове «математика»?
Решение:
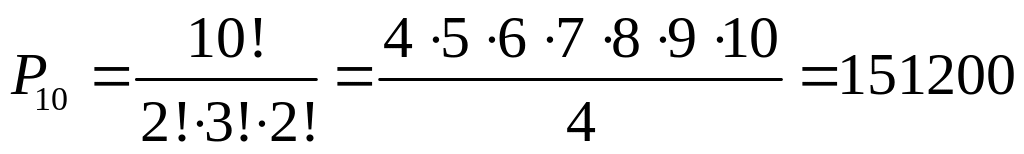
Сочетания с повторениями
Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n+m-1) различных элементов по m элементов:
Пример.
Найти число сочетаний с повторениями из четырех элементов a, b, c, d по 3 элемента.
Решение:
Искомое
число будет
Бином Ньютона
Для произвольного положительного целого числа n справедлива следующая формула:
.
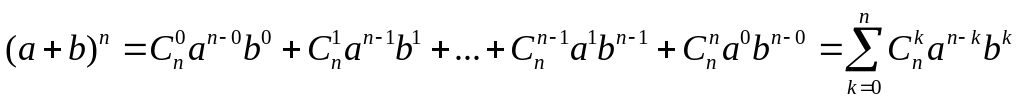Это
бином Ньютона. Коэффициенты
называются биномиальными коэффициентами.
При
n
= 2 получим формулу
;
При
n
= 3 получим формулу
.
Пример.
Определить
разложение
при
n=4.
Решение:
.
Биномиальные коэффициенты обладают рядом свойств:
;
;
;
.
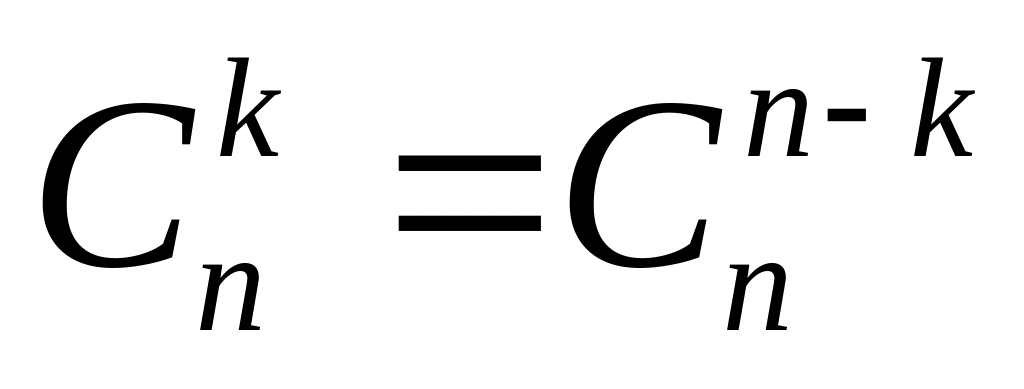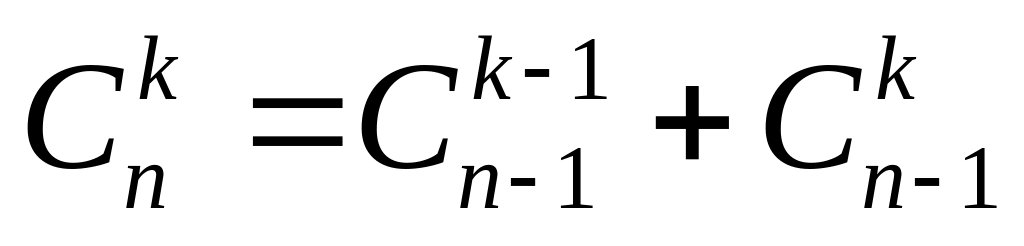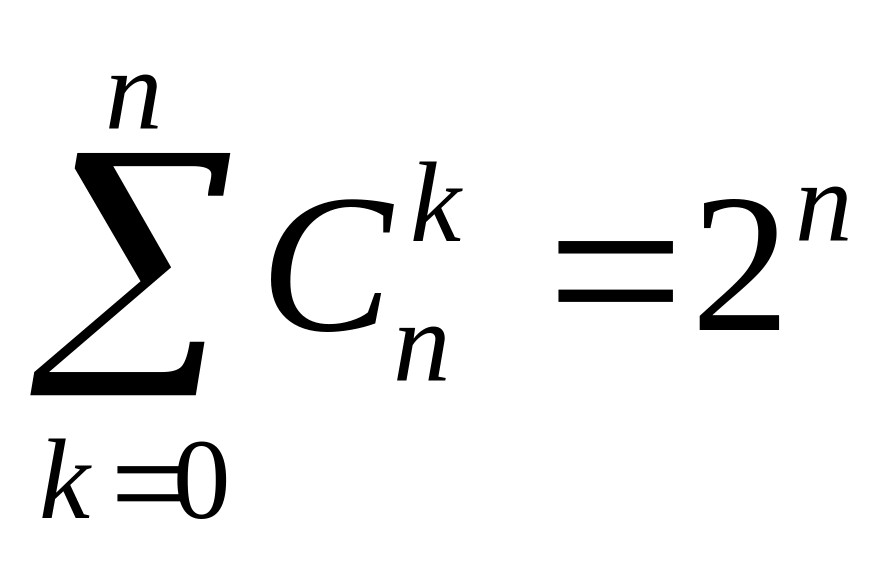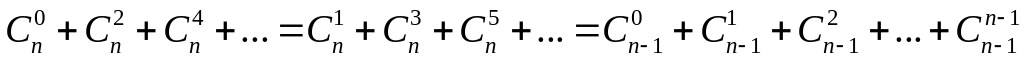Рассмотрим следующий треугольник:
………………………….
Строка под номером
n
содержит биномиальные коэффициенты
разложения
.
Воспользовавшись свойством
,
можно заметить, что каждый внутренний
элемент треугольника равен сумме двух
элементов, расположенных над ним, а
боковые элементы треугольника – единицы:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……………………….
Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов.
Решение примеров рекомендуется выполнять в среде табличного процессора MS Excel. При этом надо учитывать некоторую терминологическую путаницу.
В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)
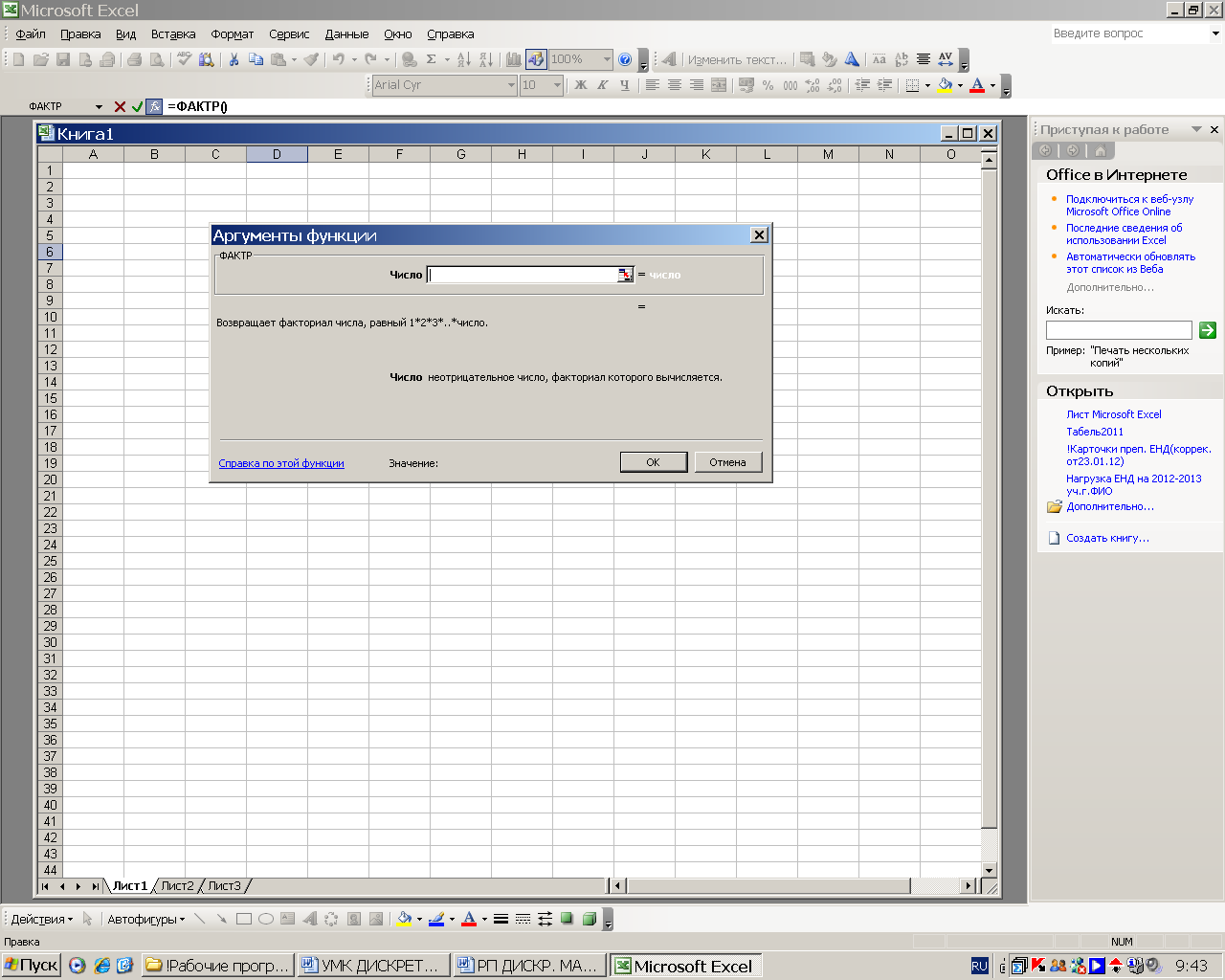
Рис. 1
В Excel считать «перестановки», т.е. размещения, очень удобно, не нужно даже вычислять факториалы (см. рис. №2 и №3): «=ПЕРЕСТ(N;K)». Вместо N и K задаются целые положительные числа, N≥K.
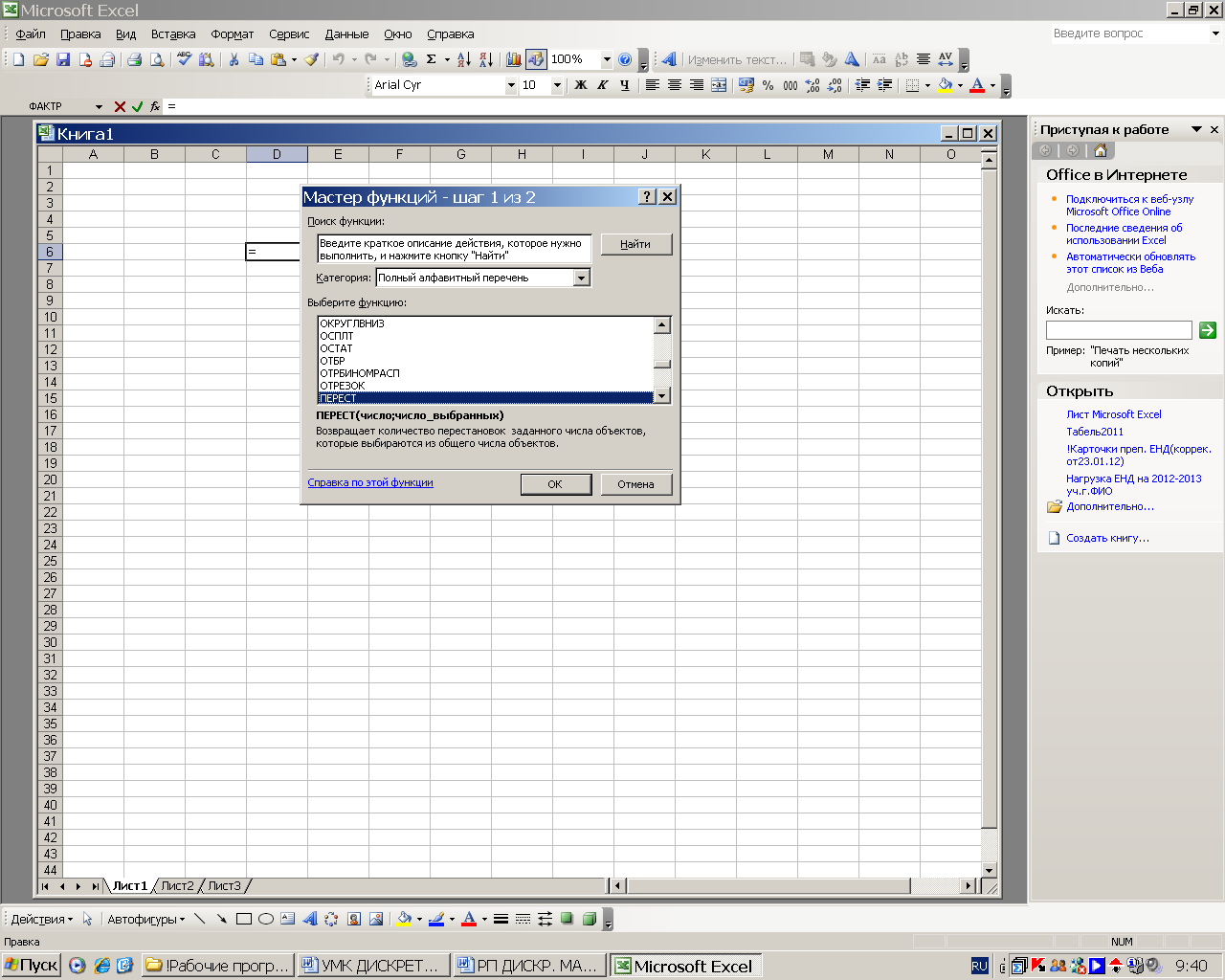
Рис. 2
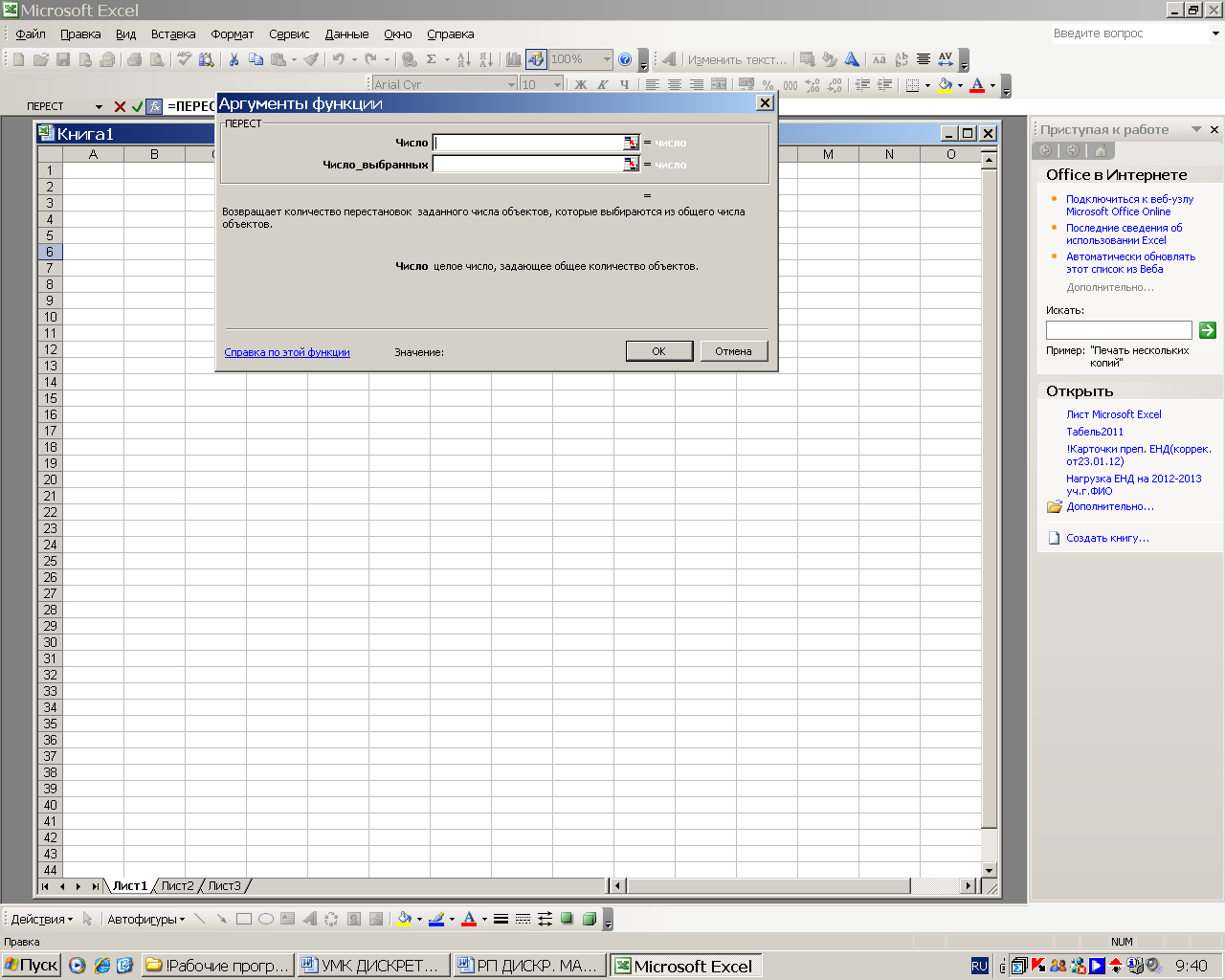
Рис. 3
Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)
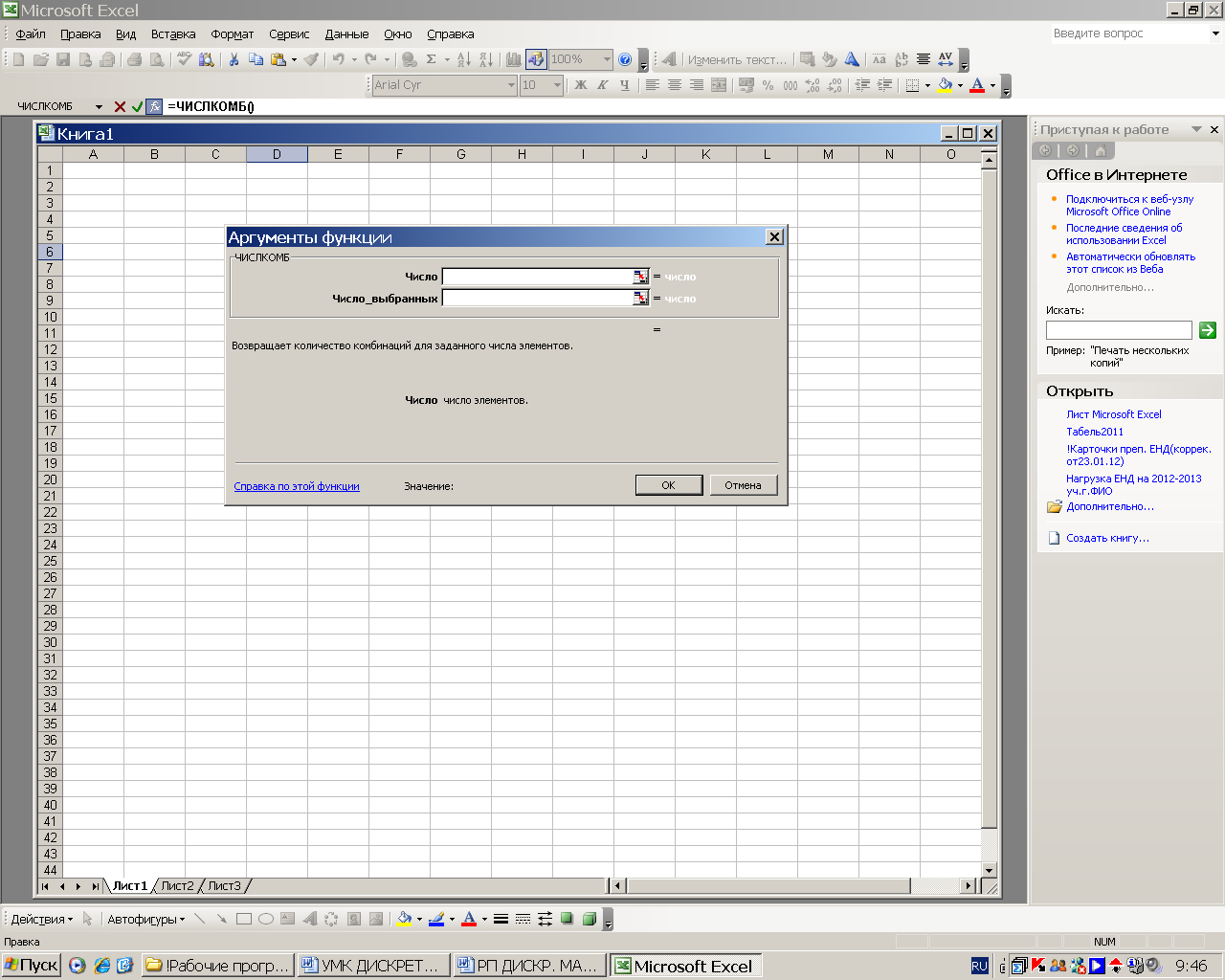
Рис. 4
При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:
