Размещения

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.

Число размещений из n элементов по m элементов обозначают (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:

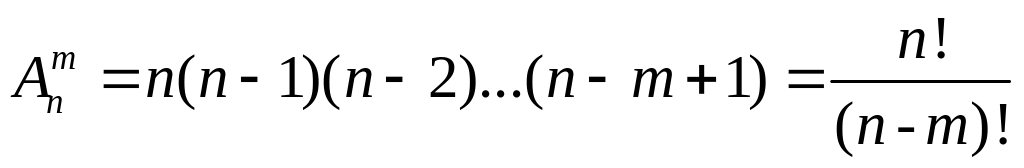
Понятие факториала

Произведение n натуральных чисел от 1 до n обозначается символом n! (n факториал), то есть

Например, 2!=

3!=

5!=

Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1.

Примеры:

Из последних двух формул следует, что

Пример.

В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки?

Решение: Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда

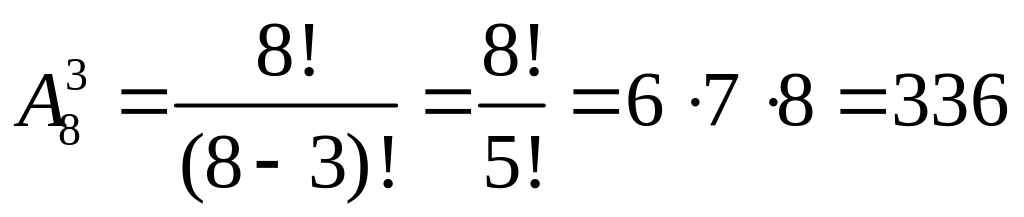(вариантов).

Пример.

Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов?

Решение:

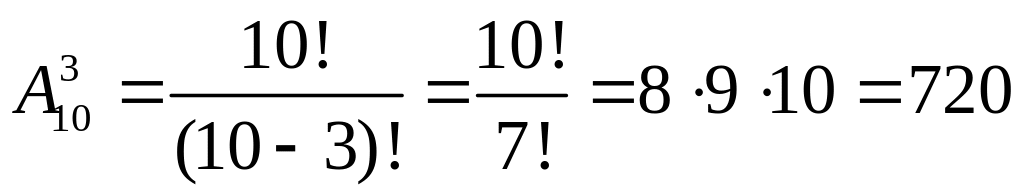(способов).

Пример.

Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными?

Решение:

(телефонных номеров).

Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.

Число всех возможных перестановок из n элементов обозначают P_n (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле:

Пример.

В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега?

Решение:

В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда (вариантов)

Пример.

Сколькими различными способами могут разместиться на скамейке10 человек?

Решение:

(способов)

Пример.

Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов?

Решение:

(способов).

Сочетания

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.

Число сочетаний вычисляют по формуле: (С - первая буква французского слова combinasion).

Пример.

Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?

Решение:

(способов).

Пример.

Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей?

Решение:

(способов).

Другой вид формул числа размещений и числа сочетаний

; , то есть .

Свойства числа сочетаний:

1)

2)

3)

4)

5)

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.

Правило произведения. Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана nk способами.

Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Размещения с повторениями

Число размещений по m элементов с повторениями из n различных элементов равно n^m, то есть

Пример.

Из цифр 1,2,3,4,5 можно составить 5³ =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры.