Код дерева [6]
Каждому дереву с m рёбрами можно взаимно однозначно сопоставить вектор длины 2m из нулей и единиц, называемый кодом дерева. Обходим дерево, начиная с корня дерева. По каждому ребру нужно пройти дважды. Первый проход по ребру отмечается нулём. Повторному проходу по ребру соответствует единица. Из всех возможных вариантов продолжения обхода выбирается продолжение обхода по крайнему левому ребру. Заканчивается обход в конце дерева. Необходимо отметить, что количество нулей в коде дерева равно количеству единиц.
Пример.
Определить код, соответствующий следующему дереву:
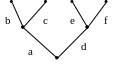
Решение: обозначим ребра буквами латинского алфавита. Тогда обход дерева задаётся следующей последовательностью: a, b, b, c, c, a, d, e, e, f, f, d. По этой последовательности (двигаясь слева направо) построим код дерева. Если буква встречается в последовательности первый раз, то вместо неё пишем 0. Буквам, которые повторяются в последовательности, соответствует 1. Тогда код дерева равен 001011001011.
По коду дерева можно восстановить само дерево. Двигаемся по последовательности из нулей и единиц слева направо. Если очередной символ равен нулю, то рисуем новое ребро. Если символ равен единице, то делаем шаг в обратном направлении по последнему ребру.
Пример. Коду 00011001011101 соответствует следующее дерево:
Планарным графом называется граф, который можно изобразить на плоскости без пересечения рёбер. Конкретное изображение планарного графа без пересечения рёбер, называется его укладкой.
Максимальный участок плоскости, любые две точки которого можно соединить кривой, не пересекающей ребра графа, называется гранью укладки планарного графа. Внешняя часть графа также является его гранью.
Плоский граф – это граф, уже уложенный на плоскости. Приведём пример планарного графа и его укладки на плоскости. Этот граф имеет 4 грани.
Теорема Эйлера. Пусть Г – множество граней укладки связного планарного графа G =(V, X). Тогда │V│-│X│+│Г│= 2, где │V│- число вершин, │X│ - число рёбер.
Следствие 1. Граф не является планарным.
Следствие 2. Граф не является планарным.
Задачи для самостоятельного решения
Является ли следующий граф деревом?
Определить, какое дерево соответствует коду:
а) 0001101011;
б) 0100101101;
в) 0000110111;
г) 0010011011;
д) 0101010011;
е) 0010110011
Определить код, соответствующий следующему дереву:
Пусть Т – двоичное дерево с корнем.
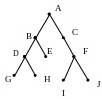
Определить: а) корень Т;
б) корень левого поддерева вершины В;
в) листья;
г) сыновей.
Выяснить, являются ли графы, задаваемые следующими матрицами смежности, деревьями:
а) A(G)
=
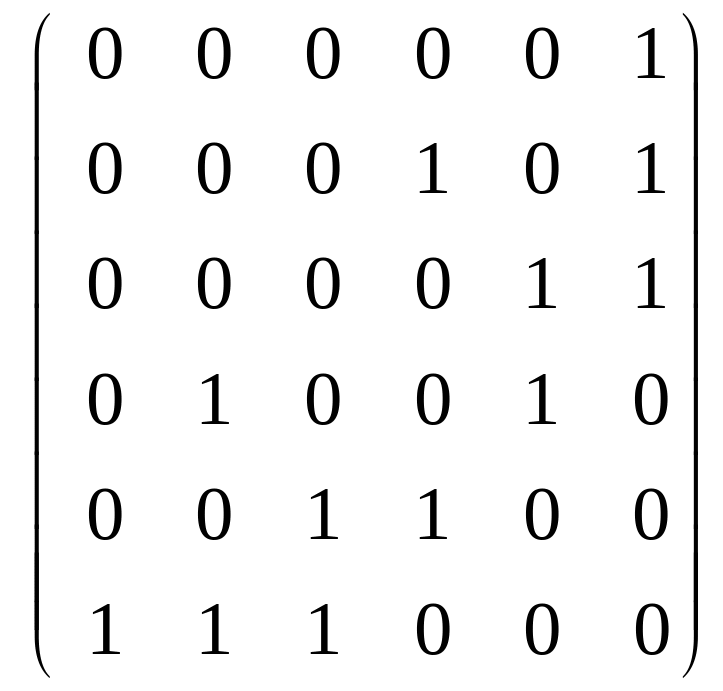
б)
A(G)
=
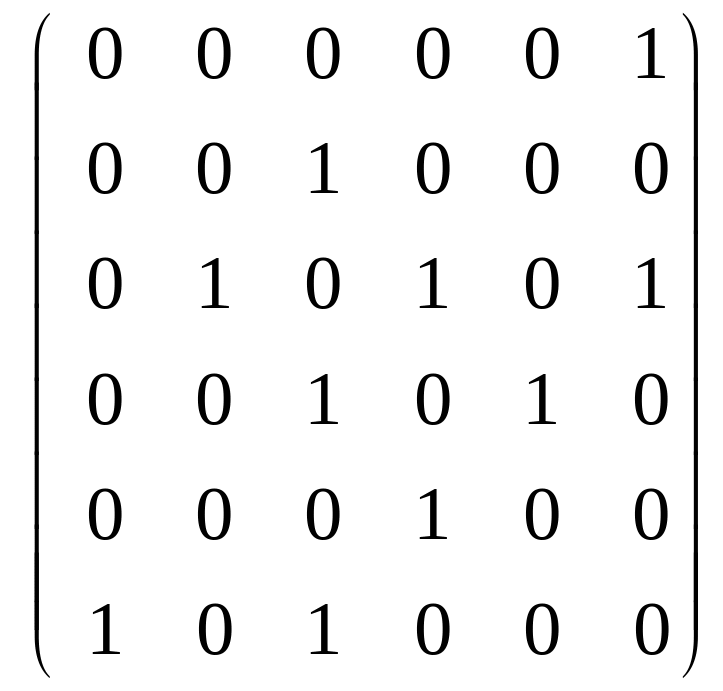
Доказать, что граф не является планарным.
Доказать, что граф не является планарным.