
- •Волгоградский кооперативный институт (филиал)
- •Дискретная математика
- •Содержание
- •Введение
- •Цели и задачи освоения учебной дисциплины
- •1. Тематический план
- •Размещения
- •Понятие факториала
- •Перестановки
- •Сочетания
- •Пример.
- •Пример.
- •Перестановки с повторениями
- •Бином Ньютона
- •Задачи для самостоятельного решения
- •Эквивалентность булевых формул.
- •Основные эквивалентности.
- •Задачи для самостоятельного решения
- •Совершенная конъюнктивная нормальная форма.
- •Минимизация дизъюнктивных нормальных форм
- •Сокращённая днф
- •Алгоритм построения сокращённой днф с помощью скнф.
- •Тупиковые и минимальные днф.
- •Алгоритм построения тупиковых и минимальных днф функции f.
- •Минимизация конъюнктивных нормальных форм
- •Минимизация в классе нормальных форм
- •Задачи для самостоятельного решения
- •Эйлеров цикл
- •Задачи для самостоятельного решения
- •Введя подходящие обозначения вершин, для каждого из графов подберите соответствующую матрицу смежности из перечисленных ниже:
- •Практическое занятие № 5 Деревья. Планарные графы. Непланарность графов и .
- •Методические указания по изучению темы
- •Код дерева [6]
- •Задачи для самостоятельного решения
- •Вопросы для подготовки к зачёту
- •Литература а) основная литература:
- •Б) дополнительная литература:
- •Дискретная математика
- •4 00002, Г. Волгоград, ул. Новосибирская, 76
Задачи для самостоятельного решения
Д
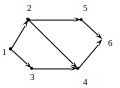 ля
графа G
построить матрицу смежности A(G)
и матрицу инцидентности B(G).
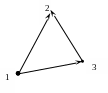
ля
графа G
построить матрицу смежности A(G)
и матрицу инцидентности B(G).
а) б)
в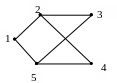
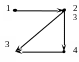 )
г)
)
г)
Введя подходящие обозначения вершин, для каждого из графов подберите соответствующую матрицу смежности из перечисленных ниже:
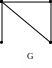


а)
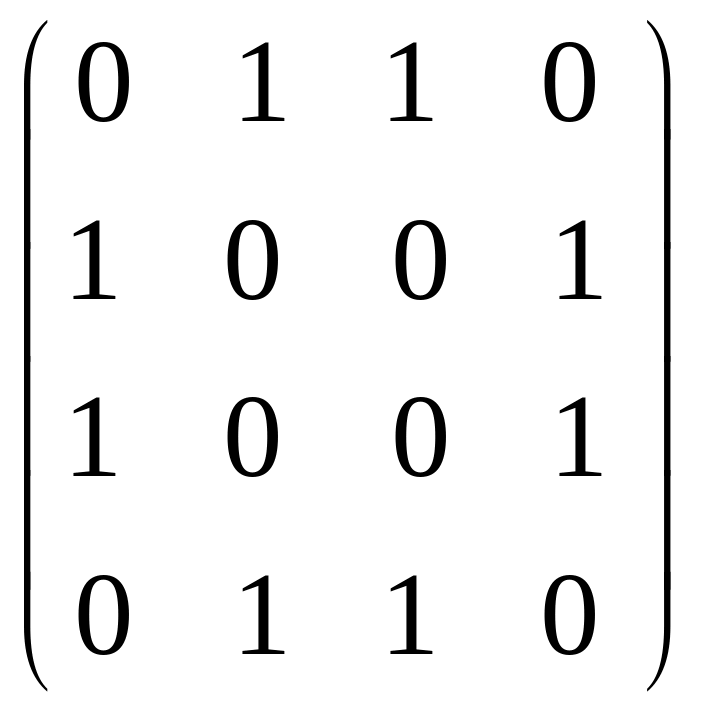 б)
б)
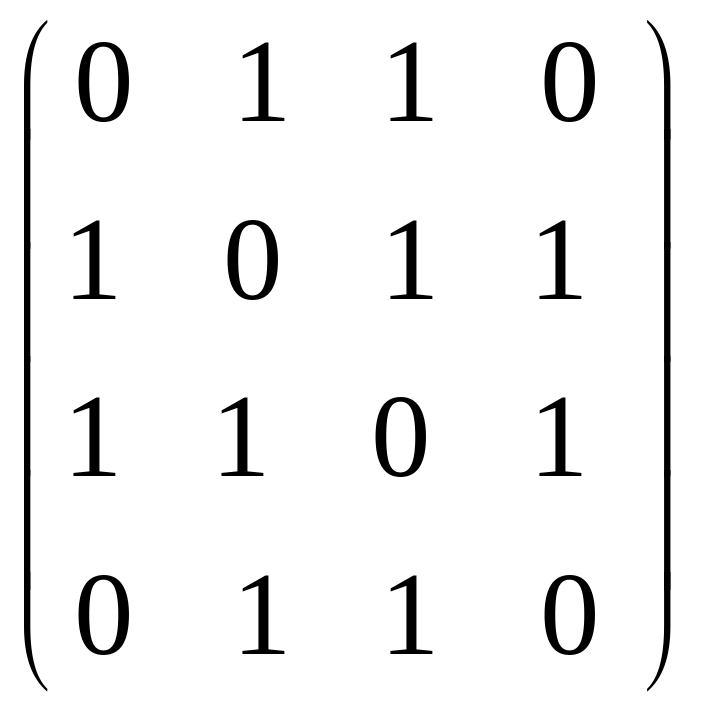 в)
в)

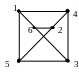
По матрице смежности построить граф.
а)
 б)
б)

в)
 г)
г)

4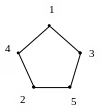 .
Изоморфны ли графы?
.
Изоморфны ли графы?
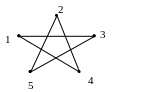
а)
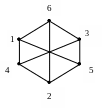
б)
Практическое занятие № 5 Деревья. Планарные графы. Непланарность графов и .
Цель занятия: уметь определять код, соответствующий данному дереву, по коду дерева восстанавливать само дерево; уметь определять число граней укладки планарного графа; доказывать планарность (непланарность) графов.
План занятия:
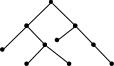
Деревья. Код дерева.
Планарные графы. Плоские графы.
Теорема Эйлера. Непланарность графов и .
Методические указания по изучению темы
Деревья являются самым распространённым классом графов, применяемых в программировании. Для них выполняются многие свойства, которые не всегда выполняются для графов в общем случае. Применительно к деревьям многие доказательства и рассуждения оказываются намного проще. Выдвигая какие-то гипотезы при решении задач теории графов, целесообразно сначала их проверять на деревьях.
Граф связен, если любые две его вершины можно соединить цепью. Если граф не связен, то его можно разбить на отдельные связные подграфы, которые называются компонентами связности.
Лес – это ациклический граф, то есть граф, в котором нет цикла. Связные компоненты леса являются деревьями.
Дерево – это связный ациклический граф. Простейшее дерево состоит из двух вершин, соединённых ребром. Каждый раз, когда добавляется ещё одно ребро, в конце его прибавляется также и вершина. Следовательно, дерево с n вершинами имеет n-1 ребро.
Например, граф G не является деревом, так как содержит цикл:

G
Утв. 1. В графе существует цикл тогда и только тогда, когда найдутся две его вершины, которые можно соединить двумя различными простыми путями.
Утв. 2. Связный граф – дерево тогда и только тогда, когда любые две его вершины можно соединить единственным простым путём.
Утв. 3. В любом дереве существует по крайней мере одна висячая вершина.
Утв. 4. Если граф G =(V, X) – дерево, то между количеством вершин и ребер справедливо следующее соотношение: | V | = | X | + 1, то есть у любого дерева число вершин на единицу больше числа его рёбер.
Остовным деревом графа G называется такой его подграф, который является деревом и содержит все вершины графа.
Дерево с одной выделенной вершиной называется деревом с корнем, а выделенная вершина – его корнем.
Вершины, стоящие непосредственно под вершиной v (и соединённые с ней рёбрами), называются сыновьями вершины v.
Вершины, расположенные в самом низу дерева (они не имеют сыновей) называются листьями.
Вершины, отличные от корня и листьев, называются внутренними вершинами графа.
Глубиной вершины v дерева с корнем Т принято считать длину единственного маршрута, соединяющего её с корнем.
Глубиной графа Т называют максимальную глубину его вершин.
Для приложения к информатике наиболее важны так называемые двоичные или бинарные деревья с корнем.
Двоичное дерево отличает от остальных то, что каждая его вершина имеет не более двух сыновей. В двоичном дереве с корнем вниз от каждой вершины идёт не более двух рёбер.
