Минимизация в классе нормальных форм

Для того, чтобы построить минимальную нормальную форму (МНФ) функции f, необходимо выполнить следующие действия:

1. Построить все минимальные ДНФ функции f.

2. Найти все минимальные КНФ функции f.

3. Из полученных форм нужно выбрать форму с наименьшим числом переменных и отрицаний переменных. Это и есть минимальная нормальная форма (МНФ) функции f.

Пример.

Построить минимальную нормальную форму (МНФ) функции f из примера (*)

Решение: Минимальная ДНФ функции f равна и содержит 5 переменных и отрицаний переменных. Обе минимальные КНФ функции f ( и ) содержат по 6 переменных и отрицаний переменных. Поэтому минимальная нормальная форма функции f совпадает с минимальной ДНФ функции f и равна

.

Задачи для самостоятельного решения

1. Построить СДНФ, СКНФ, сокращённую ДНФ, тупиковую и минимальную ДНФ, минимальную КНФ, минимальную нормальную форму для функции f, таблица истинности которой имеет следующий вид:

а).

x	y	z
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

б).

x	y	z
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

в).

x	y	z
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

г).

x	y	z
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

д).

x	y	z
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Практическое занятие №4

Основные понятия теории графов.

Матрицы смежности и инцидентности для графа и орграфа.

Цель занятия: знать основные определения теории графов, уметь строить для конкретного графа матрицу смежности и матрицу инцидентности, а также восстанавливать граф по матрице смежности.

План занятия:

1. Основные понятия теории графов.

2. Матрица смежности для графа и орграфа.

3. Матрица инцидентности для графа и орграфа.

Методические указания по изучению темы

Существует ряд задач, которые необходимо представлять в виде графических структур. Методы теории графов широко применяются в дискретной математике. Без них невозможно обойтись при анализе и синтезе различных дискретных преобразователей: функциональных блоков компьютеров, комплексов программ и т. д.

Графом G называется пара (V, X), где V- некоторое непустое множество, X - множество, состоящее из пар элементов множества V. Пары во множестве X могут повторяться, и также могут повторяться элементы в парах. Элементы множества V называют вершинами графа, а элементы множества X называют рёбрами графа. Таким образом, множества V и X задают граф G =(V, X).

Если элементы в парах множества X не упорядочены, то граф называют неориентированным графом. Если они упорядочены, то граф является ориентированным графом или орграфом, а элементы множества X называют дугами. Графически граф задаётся в виде точек и линий, их соединяющих. В ориентированном графе каждая дуга имеет направление, показанное стрелкой.

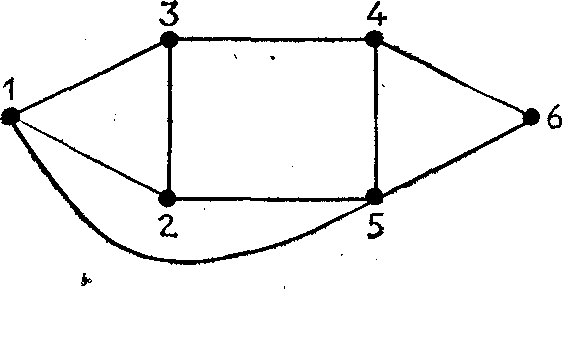
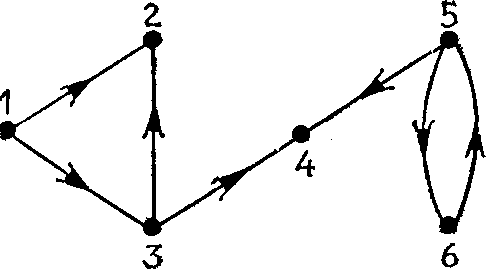
Неориентированный и ориентированный графы

Ребро, начало и конец которого совпадают, называется петлёй.

Рёбра называются кратными, если они соединяют одинаковые вершины.

Псевдограф – граф, в котором допускаются как петли, так и кратные рёбра.

Мультиграф – граф, в котором допускаются только кратные рёбра, но нет петель.

Две вершины графа называются смежными или соседними, если существует ребро, соединяющее их.

Если вершина является началом или концом ребра, то вершина и ребро называются инцидентными.

Степенью вершины называется число инцидентных ей рёбер. Степень вершины v обозначается d(v).

Вершина, степень которой равна нулю, называется изолированной.

Вершина, степень которой равна единице, называется висячей или тупиковой.

Н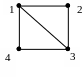 апример, для графа G степени вершин: ;

;

;

.

В орграфе вместо степени вершины вводится понятие полустепеней исхода и захода. Если вершина является началом дуги, то дуга называется исходящей из вершины, если концом – дуга называется заходящей. Полустепенью исхода вершины v - называется число дуг, исходящих из этой вершины, а полустепенью захода - число дуг, заходящих в вершину.

Н апример, для орграфа F

;

F ;

;

Полный граф – граф, все вершины которого смежны.

- полный граф с n вершинами.

Граф называется регулярным степени d, если все его вершины имеют степень d. Например, - это регулярный граф степени 3.

Регулярный граф, все вершины которого имеют степень 1, называется паросочетанием.

Граф называется двудольным, если множество его вершин может быть разделено на два непересекающихся подмножества таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств.

Маршрутом в графе называется последовательность вершин и рёбер, в которой конец предыдущего ребра совпадает с началом следующего. Число рёбер в маршруте определяет его длину.

Цепью называется маршрут, в котором все рёбра попарно различны.

Простой цепью называется цепь, в которой все вершины попарно различны.

Маршрут в ориентированном графе часто называют контуром, а цепь – путём.

Циклом (простым циклом) называется цепь (простая цепь), начало и конец которой совпадают.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.

Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

Подграфом графа G называется граф c множеством вершин и множеством рёбер , такой что .

Подграф называется собственным, если он отличен от самого графа.

Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины.

Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.

Диаметром графа называется максимальное расстояние между его вершинами.

Компонентой связности графа называется связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа.

Вершина графа, удаление которой повышает число компонент связности, называется точкой сочленения.

Под удалением вершины понимается удаление самой вершины и всех инцидентных ей рёбер.