3.2.3. Модели ис с дискретным временем

Многие ИС действуют циклически, ввиду чего результат измерения имеет вид:

y(t)=y(t_i)[1(t-jT)-1(t-(j+1)T)]=y(t_i)H_j, (3.32)

где j = 0, 1, 2, ...; t_j = jT.

Символом H_j обозначена функция

H_j=1(t-jT)-1[t-(j+1)T)], (3.33)

которая описывает действие выходной ступени преобразования цифровых ИС, называемой регистром. Регистр — это устройство памяти, в котором фиксируются результаты измерения за время одного цикла измерения. Регистр управляется блоком управления ИС.

Рис. 3.10. Выдача результата измерения цифровой ИС

Во время первого измерения ИС показывает результат у₀, т. е. состояние перед измерением, во время второго измерения — результат первого измерения у₁, и т. д. Это иллюстрирует рис. 3.10. Индекс j обозначает номер измерения, а Т — период (время) измерения. Время измерения поделено на элементарные временные шаги iΔt, идентифицированные порядковым но­мером i. Измерения начинаются с момента i = 0. В моменты времени iΔt может произойти: а) изменение состояния элементов ИС либо величин, описывающих это состояние; б) изменение структуры ИС.

Состояние элемента описывается величиной u_i или величинами u_ki (k = 1, 2, 3, ...) в моменты и (iΔt), а поддержание этого состояния в течение временного шага — функцией H_i (3.44), как это представлено в формуле (3.43). Примеры моделирова­ния ИС с дискретным временем показаны ниже.

Цифровой вольтметр с двойным интегрированием. Структурная схема цифрового вольтметра представлена на рис. 3.11. Картину прохождения сигналов по отдельным ступеням преобразования дает рис. 3.12. В первом периоде работы устройства осуществляется интегрирование напряжения U_x, и выходное напряжение интегратора имеет вид

(3.34)

С момента i = 0 счетчик L отсчитывает импульсы, вырабатываемые генератором импульсов:

U_г,м,=(t-it), i = ... -2, -1, 0, 1, 2, 3, …, (3.35)

а состояние счетчика в текущий момент описывается уравнением

= U_г,нt < N₀ , (3.36)

где

Nt<t<(N+1)t. (3.37)

Если к моменту времени t₁ счетчик достигнет состояния переполнения N₀, то интегрирование напряжения U_x прекращается и происходит переключение на входе интегратора напряжения U₀. Первый период измерения заканчивается, когда

(3.38)

(3.39)

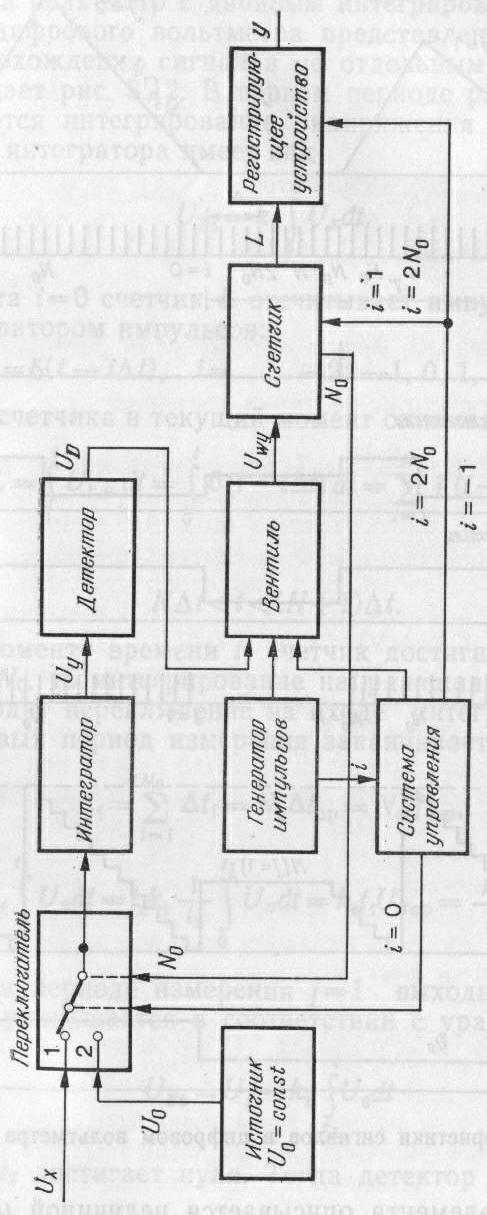
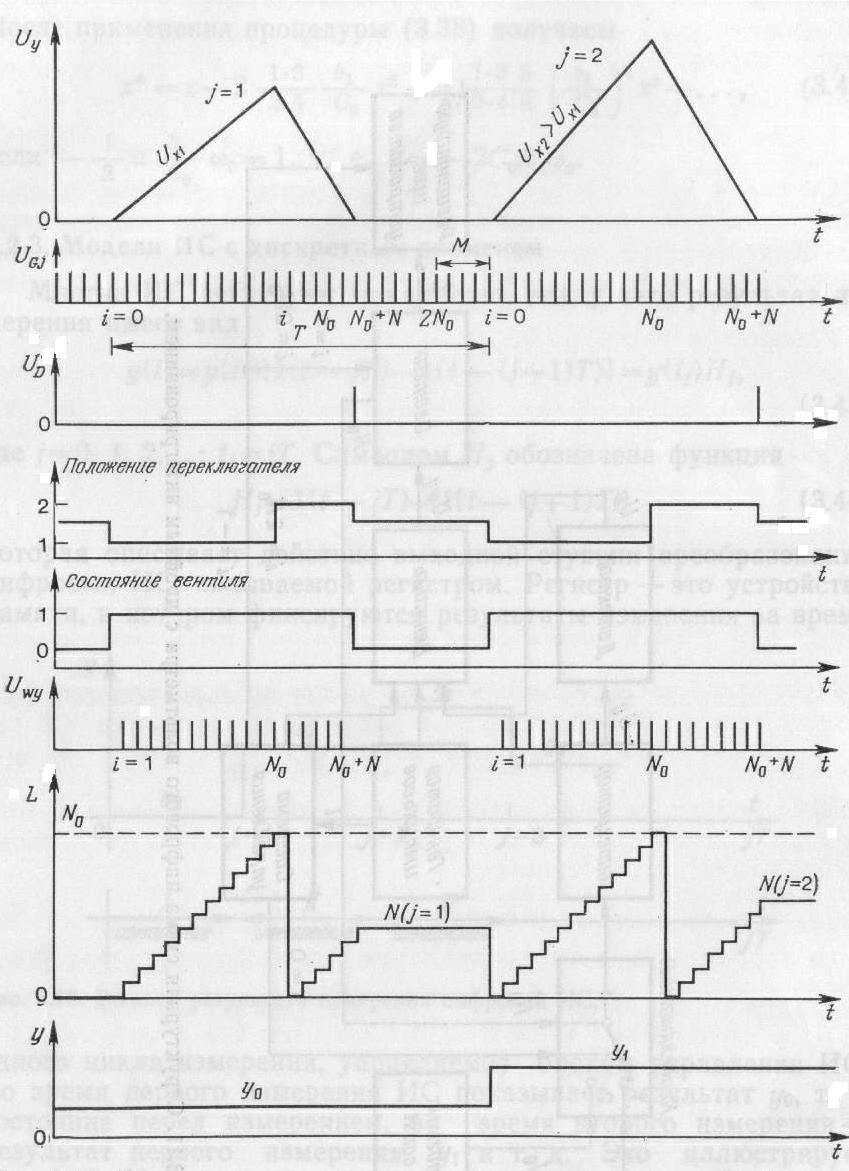
Рис. 3.12. Характеристики сигналов в цифровом вольтметре с двойным интегрированием

Во втором периоде измерения j=l выходное напряжение интегратора уменьшается в соответствии с уравнением

(3.40)

и в момент t₂ достигает нуля. Тогда детектор генерирует им­пульс

U_Д=(U_y)=(t-t₂) (3.41)

на закрытие вентиля (ключа), и последующие импульсы от генератора до счетчика не доходят.

Найдем t₂. В момент, когда интегрирование заканчивается, выходное напряжение генератора достигает порога срабатыва­ния детектора U_Д:

(3.42)

откуда с учетом (3.39) получается:

. (3.43)

Здесь U_Дx — величина нечувствительности детектора в состоянии равновесия.

В момент t₂ состояние счетчика достигает

(3.44)

при этом N соответствует условию (3.37) для момента закрытия ключа,

(N₀+N)t<t₂<(N₀+N+1)t . (3.45)

Измерение времени t₂ выполняется путем считывания временных шагов t_i, так что

(3.46)

где

0<₂t_N+1 , (3.47а)

или

0<₂ f_2N 1. (3.47б)

Отсюда после подстановки (3.43) в выражение (3.46) получаем

(3.48)

Это – уравнение преобразования интегрирующего вольтметра, где измеряемой величиной является среднее значение напряжения x=U_xср., а выходной величиной – y=N. Величина Δ_z = Δ₂f_2CP – погрешность считывания, значение которой случайно на временном интервале.

Представленная модель учитывает некоторые реальные свойства цифрового вольтметра – неодинаковые постоянные интегрирования и частоту генератора импульсов в первом и втором циклах измерения, а также нечувствительность детектора U_Д. Процедура калибровки определяется идеальной моделью, т. е. равенством (3.48) при k₁=k₂ , f_1ср.=f_2ср., U_Д=0, т. е. в идеальном случае:

(N/N₀)U₀<U^*_{x ср.}<[(N+1)/N₀]U₀. (3.49)

После подстановки в эту процедуру действительной модели (3.48) получаем

(3.50)

Время измерения составляет T=2N₀Dt+MDt, причем за Μ временных шагов осуществляются перенос состояния счетчика в регистр, обнуление счетчика и интегратора.

Уравнения преобразования (3.34), (3.36), (3.37), (3.39) позволяют определить состояние цифрового вольтметра в каждый момент времени t, так что представленная модель является динамической.