1.5.5. Стійкість сар і методи її дослідження

САР називається стійкою, якщо будучи виведеною із стану рівноваги дією, що збурює або управляє, після закінчення цієї дії повертається до колишнього положення рівноваги, або переходить в кінцеву область, що примикає до цього положення.

У теорії дослідження перехідних процесів прийнятий метод представлення шуканої часової величини X(t) у вигляді суми двох складових: примушеної і вільної:

X(t)= Xпр(t)+ Xв(t)

Примушена складова – це стале значення вихідної величини після закінчення перехідного процесу. Ця складова цілком визначається зовнішньою дією і не впливає на стійкість САР.

Вільна складова – власне перехідний процес. Ця складова визначається тільки властивостями системи і не залежить від дії. Наприклад, для аперіодичної перехідної характеристики примушена і вільна складові матимуть вигляд:

Рис. 1.20. Приклад розкладання перехідного процесу на примушену і вільну складові

Як видно з рис. 1.20, примушена складова в даному випадку – постійна величина, яка дорівнюється заданому значенню, а вільна складова – експонента, прагнуча до нуля з часом.

Очевидно, що в загальному випадку САР буде стійкою, якщо вільна складова має затухаючий характер. Тому для аналізу стійкості САР достатній аналіз лівої частини диференціального рівняння, що описує її:

(1.5.17)

і відповідного йому характеристичного рівняння:

(1.5.18)

Рішення диференціального рівняння (1.5.17) з використанням перетворення Лапласа має вигляд:

, (1.5.19)

де p_k – корені характеристичного рівняння (1.5.18), C_k – постійні інтегрування, які визначаються за початковими умовами.

Якщо серед коренів є комплексні виду p_k = α  jω, то у виразі (1.5.19) з'являються складові вигляду . Наприклад, якщо характеристичне рівняння третього порядку має 2 речовинних і 1 комплексний корінь, вільна складова відповідно до (1.5.19) матиме вигляд:

,

де p_1, p₂ – речовинні корені, α₃, ω₃ – речовинна і уявна частини третього кореня;

С₁, С₂, С₃, ψ – постійні, які визначаються за початковими умовами.

За визначенням стійкості з часом (тобто, при t→∞) вільна складова повинна затухати. Аналіз виразу (1.5.19) показує, що для цього корені характеристичного рівняння повинні відповідати наступним умовам:

- всі речовинні корені повинні бути негативними;

- речовинна частина всіх комплексних коренів повинна також бути негативною.

Хоча застосування сучасних засобів обчислювальної техніки дозволяє здійснити пряме вирішення характеристичного рівняння високих порядків, в теорії автоматичного управління відомі методи дослідження стійкості без прямого його вирішення. Це так звані критерії стійкості Гурвіца, Найквіста, Міхайлова і деякі інші (див. /1/).

1.6. Оптимізація перехідного процесу в сар з об'єктом регулювання типу «аперіодична ланка із запізнюванням»

До таких об'єктів відносяться багато промислових установок (нагрівальна піч і багато установок, пов'язаних з процесами нагріву і охолоджування, і т.д.). Структурна схема САР в цьому випадку має вигляд:

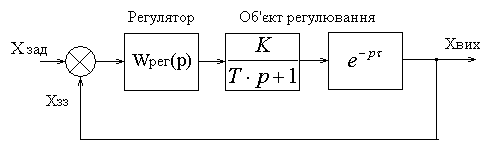
Рис. 1.21. Структурна схема САР

Об'єкт регулювання відповідно до п. 1.3.2 характеризується статичним коефіцієнтом передачі К, постійною часу Т і часом запізнювання .

Вибір типу регулятора і його настройок визначається технологічними вимогами до якості регулювання. При цьому використовують приведені в літературі (наприклад, /1/, с.216) методики вибору, засновані на детальному математичному аналізі. У основі вибору лежить величина відношення /Т:

/Т	<0,2	0,2...1	>1
Тип регулятора	Релейний (позиційний)	Неперервний (П, ПІ, ПІД)	Імпульсний

Релейний регулятор можна застосовувати за відсутності жорстких вимог до якості регулювання. У іншому випадку, навіть при співвідношенні /Т <0,2 необхідно вибирати один з безперервних регуляторів. Вибір типу регулятора можна вести з використанням номограм, приведених в довідковій літературі (наприклад, рис. 10.8 – 10.10 у /1/). При виборі типу регулятора задаються бажаним видом перехідного процесу і основними параметрами регулювання – статичною і динамічною помилками, а також часом регулювання. Прийняті наступні види перехідного процесу, для яких проведені відповідні розрахунки параметрів: аперіодичний з мінімальним часом регулювання, коливальний з 20% перерегулюванням і коливальний з мінімальною середньоквадратичною помилкою (тобто ). Настройки регуляторів різних типів для цих випадків наведені в таблиці 1.6.1.

Таблиця 1.6.1

Типові настройки регуляторів

Тип регулятора	Настройка на перехідний процес:
	Аперіодичний	20% перерегулювання
П
ПІ
ПІД