1.4.4. Пропорційно-інтегрально-диференційний (під) регулятор

Цей регулятор описується виразом:

(1.4.10)

Тут на додаток до пропорційної і інтегральної складовим додана диференціальна з своєю постійною часу Тд. Наближена перехідна характеристика ПІД-регулятора має вигляд:

Рис. 1.17. Наближена перехідна характеристика ПІД-регулятора

Наявність викиду характеристики в початковий момент часу і обумовлена наявністю диференціальної складової. На практиці це призводить до швидкої зміни подачі енергії на початку дії (наприклад, короткочасна подача повної потужності нагріву у момент включення печі). При цьому суттєво скорочується час регулювання при збереженні якості регулювання, відповідного ПІ-закону (оскільки при повільних змінах вихідної величини диференціальна складова прагне до нуля і не чинить дії на процес регулювання). Приклад реалізації ПІД-регулятора на ОП має вигляд:

Рис. 1.18. Спрощена схемна реалізація ПІД-регулятора

Як видно з рис. 1.18, сигнал розузгодження Uвх подається одночасно на входи пропорційного підсилювача DA1, інтегратора DA2 і диференціатора DA3. На виходах цих вузлів формуються відповідно напруги (–Uп), (–Uі), (–Uд). Ці напруги складаються суматором DA4, формуючи на виході напругу Uвих відповідно до виразу (1.4.10). Параметри регулятора визначаються виразами:

Кп = R2/R1, Ті = R3* Сі, Тд = R4* Сд (1.4.11)

Якісно відмінність перехідних характеристик САК з одним і тим же об’єктом і П-, ПІ- і ПІД-регуляторами показана на рис. 1.19. Тут прийнята настройка на аперіодичний перехідний процес. Як видно з рис. 1.19, П-регулятор є «найповільнішим» і має статичну похибку. ПІ- і ПІД-регулятори забезпечують астатизм системи і кращу швидкодію.

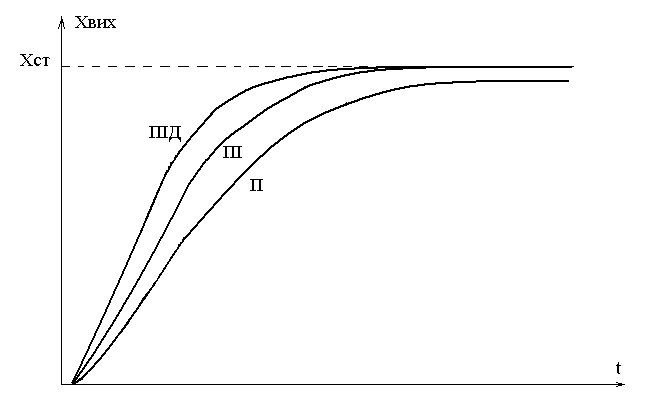
Рис. 1.19. Перехідні характеристики САК з різними типами регуляторів

Таким чином, залежно від вимог до якості регулювання і параметрів об’єкту, може бути вибраний один з типів безперервного регулятора – П, ПІ або ПІД. Очевидно, що чим складніший регулятор, тим складніше і його настройка у складі САР, тому при виборі типу регулятора доцільно рухатися від простого до складного.

1.5. Математичні основи теорії автоматичного регулювання

1.5.1. Перетворення Лапласа

Математичний опис САР уявляє собою одне або декілька диференціальних рівнянь високих порядків, пряме рішення яких утруднене. Тому в теорії автоматичного керування для дослідження САР застосовують метод, що використовує перетворення Лапласа. У цьому перетворенні часова функція X(t), звана оригіналом, замінюється функцією оператора Лапласа X(p), званою зображенням. Формули перетворення Лапласа відомі з курсу математики і мають вигляд:

а) Пряме перетворення Лапласа (перехід від оригіналу до зображення):

(1.5.1)

б) Зворотне перетворення Лапласа (перехід від зображення до оригіналу):

, (1.5.2)

де , p – оператор Лапласа, С – константа перетворення.

Перетворення Лапласа для типових функцій, часто вживаних в описі САР, зведені в таблицю.

Таблиця 1.5.1

Перетворення Лапласа для типових функцій.

№	Оригінал	Зображення	Коментарі
1	X(t)	X(p)	-
2			Зображення від підсумку оригіналів дорівнює підсумку зображень
3	A*X(t)	A* X(p)	Константа виноситься за перетворення
4			Диференціювання функції в оригіналі замінюється множенням на оператор Лапласа у зображенні: , и т.д.
5			Інтегрування функції в оригіналі замінюється діленням на оператор Лапласа в зображенні.
6			Перетворення експоненціальної функції
7	Одиничний стрибок 1(t)		Інтеграл від одиничного імпульсу.
8	Одиничний імпульс (t)	1	Похідна від одиничного стрибка – імпульс з амплітудою, прагнучою до нескінченності, тривалістю, прагнучою до нуля, і площею, яка дорівнює одиниці.

Як випливає із співвідношень, приведених в п. 4 і 5 таблиці, перетворення Лапласа дозволяє перейти від похідних і інтегралів в математичному описі САР до алгебраїчних виразів.