2.3 Приближение молекулярного поля

Наиболее простое и наивное приближение эффективного поля состоим в том, что рассматривается только один магнитный атом, а все взаимодействия этого атома с остальным кристаллом заменяются действием эффективного поля. Исторически такая теория впервые была выдвинута в 1907 г. Вейссом⁶. Он предположил, что эффективное поле

, (2.15)

где - магнитный момент образца, - постоянная молекулярного поля.

Обоснуем это предположение. Выделяя гамильтониан одного атома из (2.14), получаем:

, (2.16)

где суммирование ведется по ближайшим соседям i-ого атома; индексы у опущены, т.к. рассматривается только один тип взаимодействия. Наша цель состоит в замене взаимодействия (2.16) взаимодействием с эффективным магнитным полем, т.е.

. (2.17)

Здесь - атомный магнитный момент (оператор). Приравнивая (2.16) и (2.17), находим:

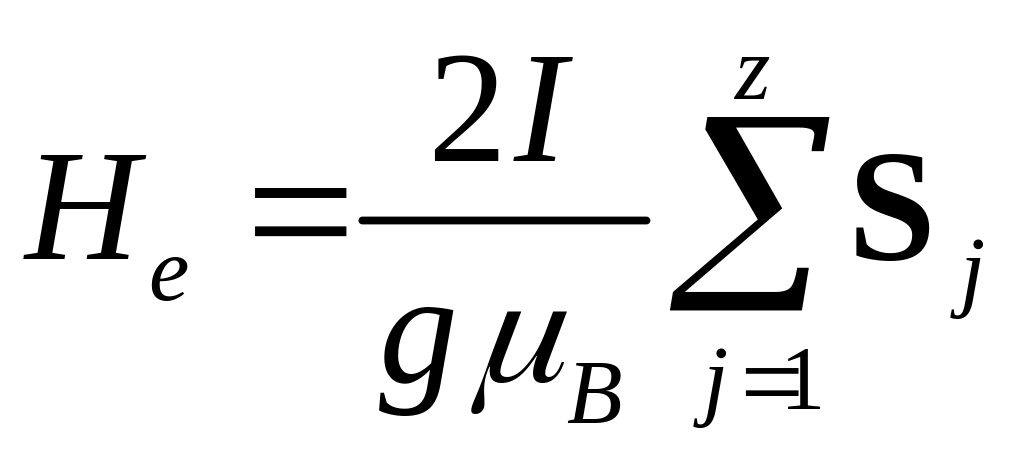. (2.18)

Далее примем, что каждый оператор можно заменить его средним значением . Если все магнитные атомы тождественны и эквивалентны, то связано с полным магнитным моментом кристалла соотношением

, (2.19)

и тогда

; (2.20)

отсюда для коэффициента , постоянной молекулярного поля, имеем:

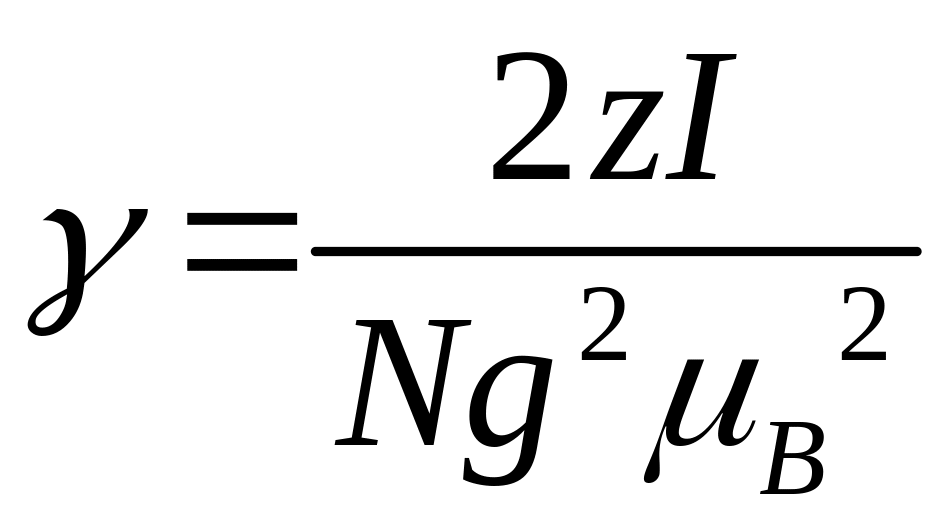. (2.21)

Таким образом, в такой модели зависит от числа атомов в образце, однако не зависит от , чего и следовало ожидать.

Необходимо учесть также внешнее приложенное поле , поэтому полное поле, действующее на i -ый атом, будет

. (2.22)

Введение понятия молекулярного поля позволяет обобщить выводы теории парамагнетизма на случай ферромагнетизма. Действительно, воспользуемся формулой для намагниченности парамагнетика, полученной в Главе 1 (см. формулу (1.57)): , где - функция Бриллюэна, а . В случае парамагнетиков мы подразумевали, что - это внешнее магнитное поле, теперь учтем еще и эффективное молекулярное поле (2.22), в итоге получаем уравнение, позволяющее описывать поведение намагниченности ферромагнетика:

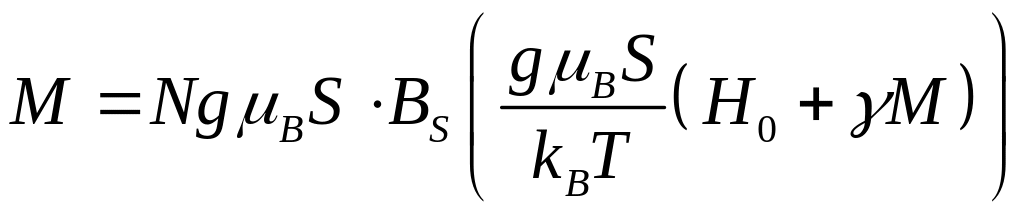. (2.23)

Проанализируем это уравнение. Поскольку стоит в аргументе функции Бриллюэна, уравнение трансцендентное и не имеет аналитического решения. Решение можно получить численно. Поведение , как функции и показано на Рис. 2.2, это поведение абсолютно типично для ферромагнетиков.

Рассмотрим некоторые важные предельные случаи уравнения (2.23).

1) При достаточно высоких температурах, когда , по аналогии с парамагнитным случаем получаем:

; (2.24)

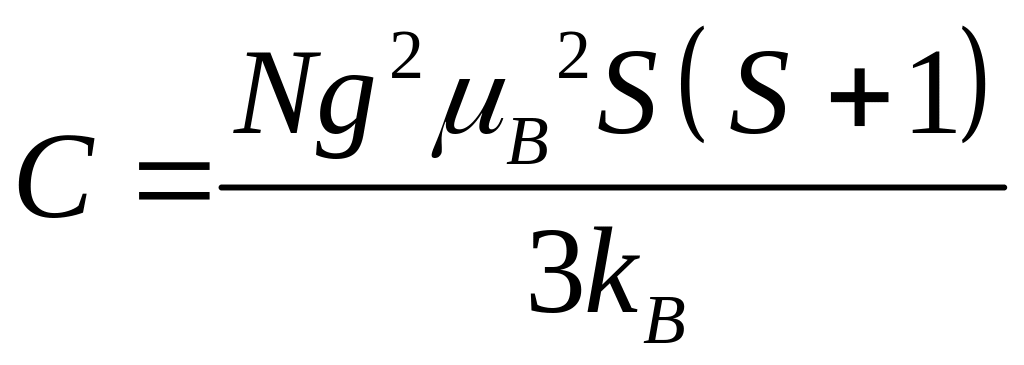; . (2.25)

П

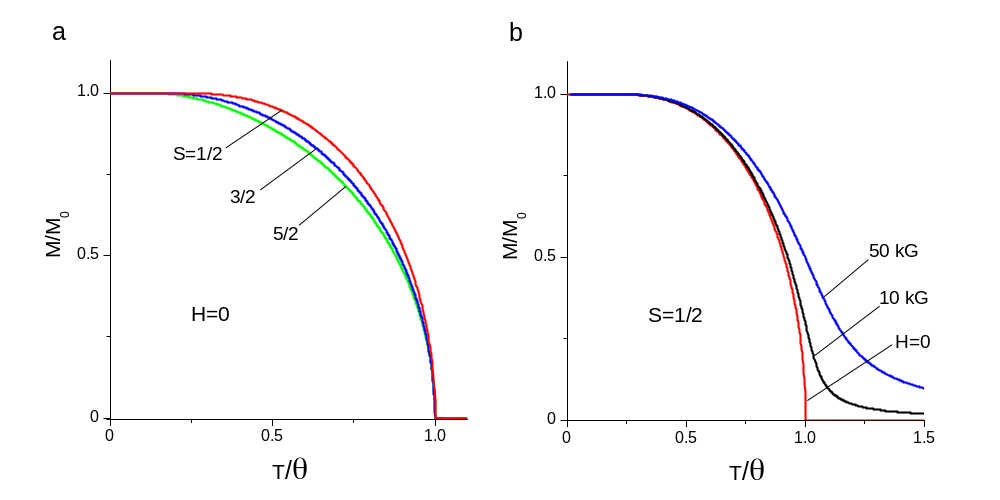
Рис. 2.2. Температурная зависимость намагниченности ферромагнетика в приближении молекулярного поля для разной величины спина (a) и магнитного поля (b).

одставляя в (2.24) выражения (2.20)-(2.22) и разрешая относительно , получаем:

.

Окончательно выражение для намагниченности имеет вид:

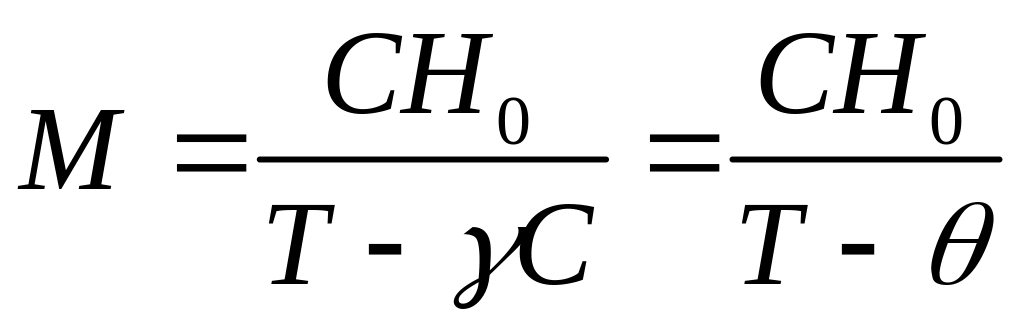, (2.25)

где

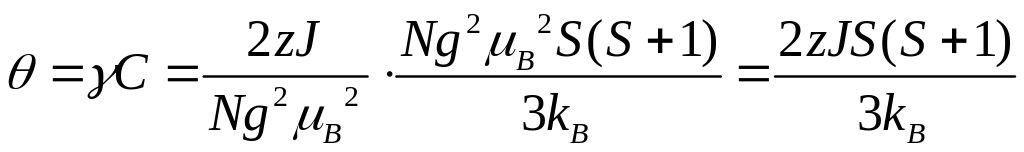. (2.26)

Соответственно для восприимчивости получаем

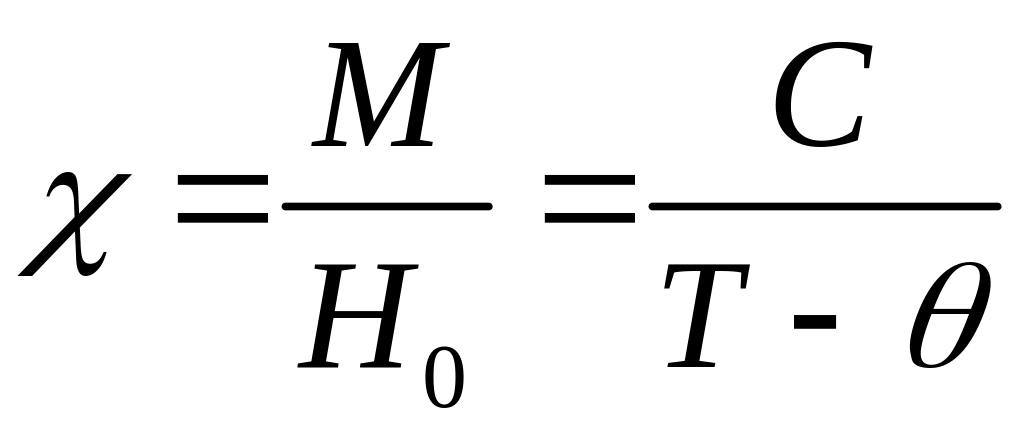. (2.27)

Э

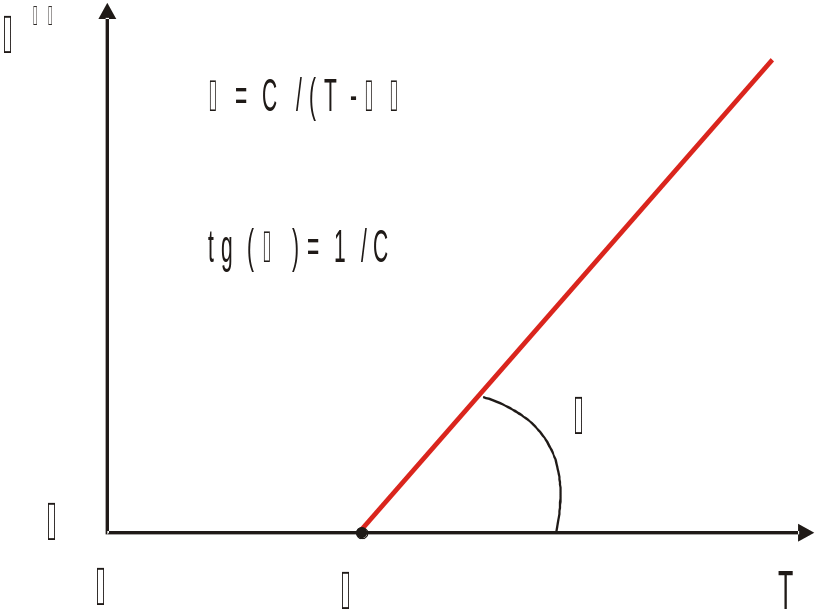
Рис. 2.3. Температурная зависимость обратной восприимчивости ферромагнетика (закон Кюри-Вейсса).

тот результат качественно согласуется с экспериментально найденным законом поведения восприимчивости ферромагнетиков при высоких температурах (парамагнитная область). Уравнение (2.25) известно под именем закона Кюри - Вейсса, а называется парамагнитной температурой Кюри. Для ферромагнетиков она положительна. Экспериментальные данные поведения восприимчивости принято графически отображать как зависимость от (Рис. 2.3). Мы должны получить при этом прямую линию с угловым коэффициентом , пересекающую ось в точке . Заметим, что и выражаются через фундаментальные величины, характеризующие ферромагнитную систему.

П ри более низких температурах, когда не является достаточно малой ( ), необходимо использовать выражение (2.23). При этом для получения зависимости приходится применять численные или графические методы решения. Аналитические решения можно получить для двух важных предельных случаев (Рис. 2.4).

2

Рис. 2.4. Два крайних предельных случая в поведении намагниченности ферромагнетика.

) . Здесь можно использовать выражение для функции Бриллюэна при больших значениях аргумента ( ): . Тогда получаем для

Аргумент можно представить в следующем виде

,

И, следовательно,

.

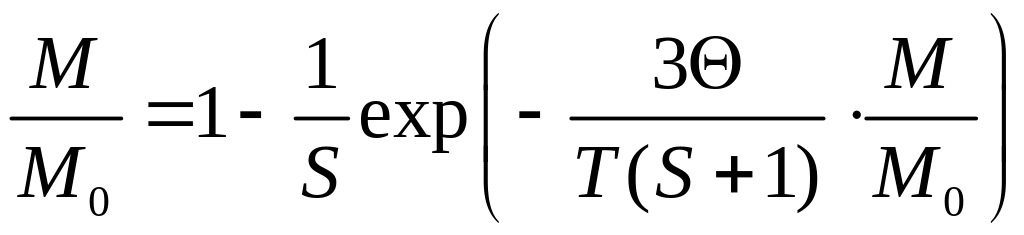С учетом того, что

,

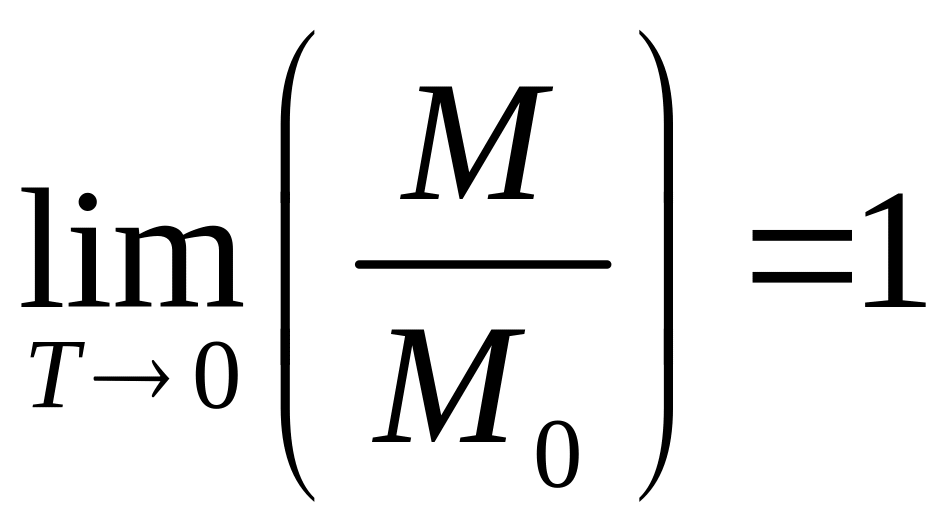получаем

. (2.28)

Таким образом, полное насыщение достигается при .

Падение с ростом температуры вблизи абсолютного нуля, согласно (2.28), оказывается гораздо более быстрым, чем это предсказывает теория спиновых волн Блоха:

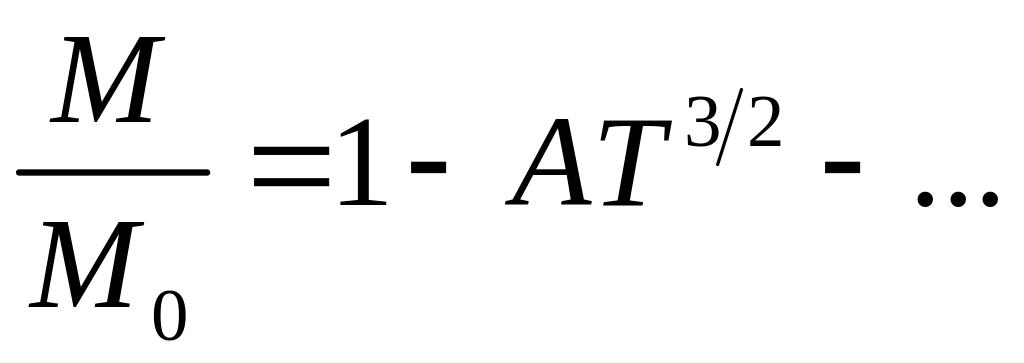. (2.29)

Она, как известно, дает точное решение для модели Гейзенберга при очень низких температурах, и экспериментальные результаты для классических ферромагнетиков с хорошей точностью подчиняются закону Блоха 3/2.

3) Случай . Посмотрим теперь, как себя ведет намагниченность вблизи температуры Кюри. Здесь можно воспользоваться разложением функции Бриллюэна при малых аргументах, в итоге получим

. (2.30)

Таким образом,

(2.31)

Этот результат качественно согласуется с экспериментальными данными по ферромагнитным материалам и используется, например, для определения точки Кюри по измерениям намагниченности, хотя более точные эксперименты показывают зависимость , но близко не к 1/2, а к 1/3.

Приведенный выше анализ поведения намагниченности позволяет сделать заключение, что теория молекулярного поля дает поразительно верную качественную картину наиболее важных фундаментальных физических свойств ферромагнетиков, а именно:

• предсказывает существование спонтанной намагниченности;

• объясняет ее температурную зависимость;

• объясняет температурный ход восприимчивости и теплоемкость.

Упомянутые выше расхождения теории с экспериментом можно частично устранить, используя усовершенствованные модели эффективного поля (см. книгу Дж. Смарта «Эффективное поле в теории магнетизма»).