Министерство образования и науки Российской Федерации

Сибирский федеральный университет

Федеральное государственное бюджетное учреждение науки

Институт физики им. Л.В. Киренского Сибирского отделения

Российской академии наук

Обменное взаимодействие. Ферромагнетизм. Приближение молекулярного поля (физика магнитных явлений)

Учебно-методическое пособие

Красноярск

СФУ

2012

УДК 537.622.4(07)

ББК 22.373.2я73

О 193

Составители Волков Н.В., Попков С. И.

О 193 Обменное взаимодействие. Ферромагнетизм. Приближение молекулярного поля: учебно-методическое пособие [Электронный ресурс] / сост. Н. В. Волков, С. И. Попков. – Электрон. дан. – Красноярск: Сиб. федер. ун-т, 2012. – Систем. требования: PC не ниже класса Pentium I; 128 Mb RAM; Windows 98/XP/7; Adobe Reader V8.0 и выше. – Загл. с экрана.

Учебно-методическое пособие подготовлено для студентов 4 курса кафедры физики конденсированного состояния вещества Института инженерной физики и радиоэлектроники Сибирского федерального университета, слушающих курс лекций «Физика магнитных явлений». В пособии даны кратко основные представления о причинах возникновении магнитного порядка в веществах, об обменном взаимодействии. Изложена теория молекулярного поля. Пособие дает знания, необходимые для успешного освоение курса «Физика магнитных явлений», «Магнитные измерения», Квантовая теория магнетизма и др.

Предназначено для студентов, обучающихся по программам 011200.68.02 Физика конденсированного состояния вещества; 011200.68.06 Физика магнитных явлений.

УДК 537.622.4(07)

ББК 22.373.2я73

© Сибирский

федеральный

университет, 2012

Учебное издание

Подготовлено к публикации издательским центром

БИК СФУ

Подписано в свет 7.11.2012 г. Заказ 10344.

Тиражируется на машиночитаемых носителях.

Редакционно-издательский отдел

Библиотечно-издательского комплекса

Сибирского федерального университета

660041, Г. Красноярск, пр. Свободный, 79

Тел/факс (391)206-21-49. E-mail rio@sfu-kras.ru

http://rio.sfu-kras.ru

Оглавление

Аннотация. 4

2.1. Обменная энергия 5

2.2. Модель Гейзенберга 8

2.3 Приближение молекулярного поля 12

Контрольные вопросы 19

Задачи 19

Список литературы 21

Аннотация.

Учебно-методическое пособие подготовлено для студентов 4 курса кафедры физики конденсированного состояния вещества Института инженерной физики и радиоэлектроники Сибирского федерального университета, слушающих курс лекций «Физика магнитных явлений». В пособии даны кратко основные представления о причинах возникновении магнитного порядка в веществах, об обменном взаимодействии. Изложена теория молекулярного поля. Пособие дает знания, необходимые для успешного освоение курса «Физика магнитных явлений», «Магнитные измерения», Квантовая теория магнетизма и др.

2. Обменное взаимодействие. Ферромагнетизм. Приближение молекулярного поля.

2.1. Обменная энергия

Идея о том, что спонтанная намагниченность обязана своим происхождением специфическому взаимодействию между магнитными атомами, была выдвинута впервые Пьером Вейссом¹ в 1907 г. Однако магнитные дипольные взаимодействия, которые он имел в виду, оказались слишком малыми, чтобы объяснить величину наблюдавшихся температур перехода. Только после возникновения квантовой механики Гейзенберг² и др. показали, что эти взаимодействия имеют квантовомеханическую природу и являются прямым следствием ограничений, накладываемых на волновые функции принципом Паули³. Именно этот принцип требует, чтобы электронные волновые функции были антисимметричны относительно перестановки пространственных и спиновых координат пары электронов, причем оказывается, что это требование делает собственные значения зависящими от относительной ориентации спинов электронов. Этот эффект можно рассматривать как некоторое «взаимодействие», ориентирующее спиновые моменты количества движения (а следовательно, и магнитные моменты) атомов.

Простейший пример этого эффекта дает квантовомеханическое рассмотрение системы двух электронов. Предположим, что мы имеем систему двух электронов, подверженных действию полей, происходящих от одинаковых потенциальных функций. Оператор Гамильтона пары электронов записывается в виде

, (2.1)

где индексы 1 и 2 относятся к пространственным координатам соответствующих электронов, а - расстояние между электронами. Первые два члена представляют собой кинетическую энергию электронов, следующие два члена – потенциальная энергия электронов, последний член – энергия кулоновского взаимодействия электронов. Если вначале пренебречь взаимодействием между электронами, то получим волновое уравнение в виде

. (2.2)

Оно разделяется на два независимых волновых уравнения для каждого из электронов. Эти уравнения имеют решения

, (2.3)

где и - волновые функции отдельного электрона в поле потенциала . Если применить теорию возмущений в первом порядке для вычисления влияния взаимодействия, то получим:

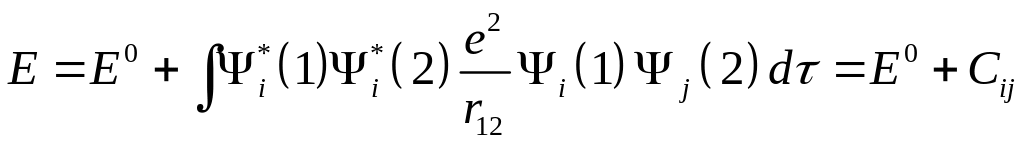, (2.4)

где можно интерпретировать как среднее значение кулоновского взаимодействия двух электронов в состояниях i и j соответственно.

Однако этот результат получен без учета принципа Паули, который требует, чтобы полная волновая функция была антисимметричной по отношению к обмену пространственных и спиновых координат двух электронов. Элементарная квантовая механика электронных спинов показывает, что при комбинировании двух спинов с получаются два состояния, характеризуемые полным спином . Синглетное состояние ( ) антисимметрично, а триплетное состояние ( ) симметрично по спиновым координатам. Укажем без доказательства (его можно найти в любом курсе квантовой механики), что соответствующие полные волновые функции имеют вид

; (2.5)

, (2.6)

где - спиновая функция. Эти две функции соответствуют одному вырожденному уровню энергии, но если уже с этими волновыми функциями вычислить поправку первого порядка теории возмущения, то получим:

; (2.7)

, (2.8)

где

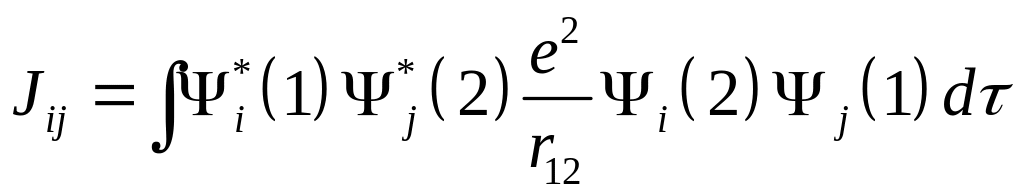(2.9)

- величина, получившая название обменной энергии двух электронов в состояниях i и j. Таким образом, энергии синглетного (спины «антипараллельны», ) и триплетного состояния (спины «параллельны», ) оказываются различными. Энергия какого из состояний, синглетного или триплетного, меньше и, следовательно, соответствует основному состоянию рассматриваемой системы, зависит от знака .

В рассматриваемом нами конкретном случае знак всегда должен быть положителен, а значит, взаимодействие будет носить ферромагнитный характер, Рис. 2.1. В более общих случаях может быть больше нуля и меньше нуля.

В

Рис. 2.1. Схематическая электронная структура, поясняющая возникновение обменного взаимодействия в случае двух электронов в одинаковом потенциальном поле.

ычисления, подобные приведенным выше, впервые были проведены Паули для атома He, а также Гайтлером и Лондоном для молекулы водорода. В обоих случаях синглетное состояние лежит ниже, и .