5.2.2. Временная диаграмма

Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 27).

i(t) = I_m sin(ωt - ψ_i).

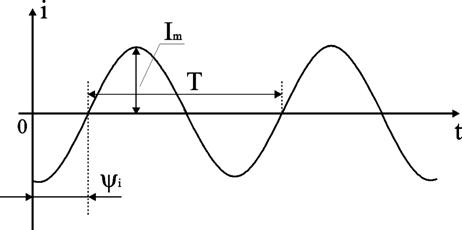
Рис. 27 Временная диаграмма

5.2.3. Графоаналитический способ

Рис. 28 Графические синусоидальные величины

Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 28). Предполагается вращение против часовой стрелки с частотой вращения ω. Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины.

Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.

Векторные величины отмечаются точкой над соответствующими переменными.

Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.

В основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм.

5.2.4. Аналитический метод с использованием комплексных чисел

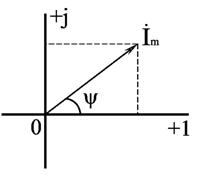Рис. 29 Синусоидальный ток i(t) на комплексной плоскости

Синусоидальный ток i(t) = I_m sin(ωt + ψ) можно представить комплексным числом Í_m на комплексной плоскости (рис. 29)

Í_m = I_me^jψ, где амплитуда тока I_m – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.

Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.

5.3. Сопротивления в цепи переменного тока

В цепях переменного тока выделяют следующие виды сопротивлений.

Активное. Активным называют сопротивление резистора. Условное обозначение R.

Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты.

Реактивное. В разделе реактивные выделяют три вида сопротивлений: индуктивное xL и емкостное хс и собственно реактивное. Для индуктивного сопротивления выше была получена формула X_L = ωL. Единицей измерения индуктивного сопротивления также является Ом. Величина xL линейно зависит от частоты.

Для емкостного сопротивления выше была получена формула X_C = 1 / ωC. Единицей измерения емкостного сопротивления является Ом. Величина хс зависит от частоты по обратно-пропорциональному закону. Просто реактивным сопротивлением цепи называют величину X = X_L - X_C.

Полное сопротивление. Полным сопротивлением цепи называют величину:

(2.4)

.

Из этого соотношения следует, что сопротивления Z, R и X образуют треугольник: Z – гипотенуза, R и X – катеты. Для удобства в этом треугольнике рассматривают угол φ, который определяют уравнением:

(2.5)

φ = arctg((X_L - X_C) / R), и называют углом сдвига фаз. С учетом него можно дать дополнительные связи:

(2.6)

R = Z cos φ,

(2.7)

X = Z sin φ.

5.4. Цепь с последовательным соединением элементов

Проведем анализ работы электрической цепи с последовательным соединением элементов R, L, С.

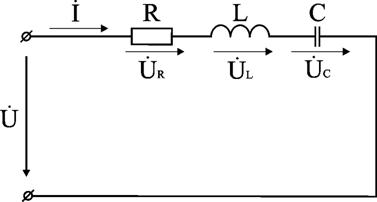
Рис. 30 Цепь с последовательным соединением элементов

Предположим, что в этой задаче заданы величины R, L, С, частота f, напряжение U. Требуется определить ток в цепи и напряжение на элементах цепи. Из свойства последовательного соединения следует, что ток во всех элементах цепи одинаковый. Задача разбивается на ряд этапов.